論文解讀（JKnet）《Representation Learning on Graphs with Jumping Knowledge Networks》

• 2022 年 8 月 3 日
• 筆記
• 論文解讀

論文資訊

論文標題：Representation Learning on Graphs with Jumping Knowledge Networks
論文作者：Keyulu Xu, Chengtao Li, Yonglong Tian, Tomohiro Sonobe, Ken-ichi Kawarabayashi, Stefanie Jegelka
論文來源：2018,ICML
論文地址：download
論文程式碼：download

1 Introduction

　　最近，圖表示學習提出了基於 「鄰域聚合」 一系列演算法，這種演算法嚴重依賴於圖結構，本文提出了一種靈活應用不同鄰域的架構 jumping knowledge (JK) networks。

　　此外，將 JK framework 與 GCN 、GraphSAGE 和GAT 等模型相結合，可以持續提高這些模型的性能。

2 Model analysis

　　除圖屬性資訊很重要之外，子圖結構對 「鄰域聚合」 演算法同樣很重要。

　　同樣一個圖中，如果起點不同，random walk 相同步數之後的影響範圍也就不同，random walk 多少步對應的就是卷積的迭代次數。

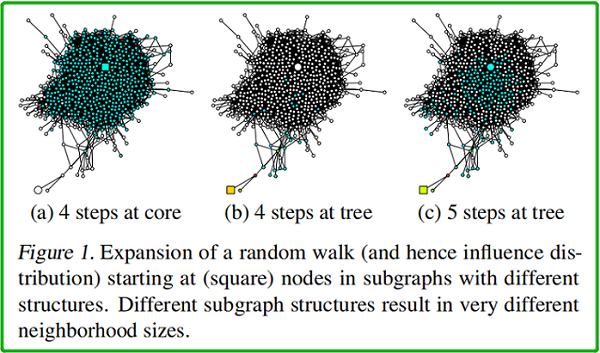
　　如上圖所示，(a)、(b)、(c) 中 均以 square node 為起點。（a）中 square node 出現在中心稠密處 [core]；（b）中出現在圖邊緣處【此時的 random walk 路徑類似於樹結構】；(c)  在 (b) 的基礎上， random walk 的終點位於中心稠密處。

　　　　$\begin{array}{l}h_{\mathcal{N}(i)}^{(l+1)}=\operatorname{aggregate}\left(\left\{h_{j}^{l}, \forall j \in \mathcal{N}(i)\right\}\right) \\h_{i}^{(l+1)}=\sigma\left(W \cdot \operatorname{concat}\left(h_{i}^{l}, h_{\mathcal{N}(i)}^{l+1}\right)\right)\end{array}$

　　→​ 是否可以自適應地調整（即學習）每個節點的受影響半徑？【可能 要減少 所謂 「鄰域」 的大小】

　　→​為實現這一點，本文探索了一種學習有選擇地利用來自不同 「鄰域」 的資訊的架構，將表示「跳轉」到最後一層。

3 Related work

3.1 neighborhood aggregation scheme

　　典型的鄰域聚合方案如下：

　　　　$h_{v}^{(l)}=\sigma\left(W_{l} \cdot \operatorname{AGGREGATE}\left(\left\{h_{u}^{(l-1)}, \forall u \in \tilde{N}(v)\right\}\right)\right)  \quad\quad\quad(1)$

3.2 Graph Convolutional Networks (GCN)

Recall 

　　two-layer GCN ：

　　　　$Z=f(X, A)=\operatorname{softmax}\left(\hat{A} \operatorname{ReLU}\left(\hat{A} X W^{(0)}\right) W^{(1)}\right)$

　　其中，$\hat{A}=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$

　　Kipf 提出的 GCN：

　　其中，$c_{j i}=\sqrt{|\mathcal{N}(j)|} \sqrt{|\mathcal{N}(i)|}$ 

　　顯然就是，$\hat{A}=\tilde{D}^{-1} \tilde{A} \quad\quad\quad(3)$ 

　　GCN 的 inductive 變形：

　　　　$\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}\right\} \cup\left\{\mathbf{h}_{\mathrm{u}}^{\mathrm{k}-1}, \forall \mathrm{u} \in \mathcal{N}(\mathrm{v})\right\}\right)\right)$

　　　　$\begin{aligned}h_{N(v)}^{(l)} &=\sigma\left(W_{l} \cdot \operatorname{AGGREGATE}_{N}\left(\left\{h_{u}^{(l-1)}, \forall u \in N(v)\right\}\right)\right) \\h_{v}^{(l)} &=\operatorname{COMBINE}\left(h_{v}^{(l-1)}, h_{N(v)}^{(l)}\right)\end{aligned} \quad\quad\quad(4)$ 

　　COMBINE 步驟是這個範式的關鍵，可以被視為不同層之間的「skip connection」的一種形式。

　　GraphSAGE 的 Mean aggregator 形式：

　　　　$\begin{array}{l}\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}\right\} \cup\left\{\mathbf{h}_{\mathrm{u}}^{\mathrm{k}-1}, \forall \mathrm{u} \in \mathcal{N}(\mathrm{v})\right\}\right)\right. \\\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W}^{\mathrm{k}} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}, \mathbf{h}_{\mathcal{N}(\mathrm{v})}^{\mathrm{k}}\right)\right)\end{array}$

3.4 Neighborhood Aggregation with Directional Biases

　　在第6節中，我們演示了我們的框架不僅適用於簡單的鄰域聚合模型(GCN)，而且還適用於跳過連接(GraphSAGE)和 帶 directional biase 的 GAT 。

4 Influence Distribution and Random Walks

　　受 sensitivity analysis 和 influence functions 的啟發，我們研究了其特徵影響給定節點表示的節點的範圍，這個範圍可以給出節點從中獲取資訊的鄰域有多大。

　　本文測量節點 $x$ 對節點 $y$ 的敏感性，或者 $y$ 對 $x$ 的影響，通過測量 $y$ 的輸入特徵的變化對最後一層 $x$ 的表示的影響程度。對於任何節點 $x$，influence distribution 捕獲了所有其他節點的相對影響。

　　Definition 3.1 (Influence score and distribution). For a simple graph $G=(V, E)$ , let $h_{x}^{(0)}$ be the input feature and $h_{x}^{(k)}$ be the learned hidden feature of node $x \in V$ at the $k-th$ (last) layer of the model. The influence score $I(x, y)$ of node $x$ by any node $y \in V$ is the sum of the absolute values of the entries of the Jacobian matrix $\left[\frac{\partial h_{x}^{(k)}}{\partial h_{y}^{(0)}}\right]$ . We define the influence distribution $I_{x}$ of $x \in V$ by normalizing the influence scores: $I_{x}(y)=I(x, y) / \sum_{z} I(x, z)$ , or

　　　　$I_{x}(y)=e^{T}\left[\frac{\partial h_{x}^{(k)}}{\partial h_{y}^{(0)}}\right] e /\left(\sum\limits _{z \in V} e^{T}\left[\frac{\partial h_{x}^{(k)}}{\partial h_{z}^{(0)}}\right] e\right)$

　　where $e$ is the all-ones vector.

　　對於 completeness ，我們還定義了 random walk distributions ：

　　Definition 3.2. Consider a random walk on  $\widetilde{G}$  starting at a node  $v_{0}$ ; if at the  $t-th$ step we are at a node  $v_{t}$ , we move to any neighbor of  $v_{t}$  (including  $v_{t}$  ) with equal probability.The $t$-step random walk distribution $P_{t}$ of $v_{0}$ is

　　　　$P_{t}(i)=\operatorname{Prob}\left(v_{t}=i\right) $

　　隨機遊動分布的一個重要性質是，當 $t$ 的增加時，它變得更加擴散，如果圖是非二部的，它收斂於極限分布。收斂速度取決於子圖的結構，並且可以受隨機遊動躍遷矩陣的譜間隙的限制。

4.1 Model Analysis

　　以下結果表明，公共聚合方案的影響分布與隨機遊動分布密切相關。這一觀察結果暗示了我們將討論的具體含義——優勢和缺點。

　　與 ReLU 激活的隨機化假設類似，我們可以繪製GCNs和隨機遊動之間的聯繫：

　　Theorem 1. Given a  $k$-layer  G C N  with averaging as in Equation (3), assume that all paths in the computation graph of the model are activated with the same probability of success  $\rho$ . Then the influence distribution  $I_{x}$  for any node  $x \in V$  is equivalent, in expectation, to the  $k$-step random walk distribution on  $\widetilde{G}$  starting at node  $x$ .

　　證明如下：

　　通過修改 Theorem 1 的證明，可以直接證明 $\text{Eq.2}$ 中 GCN 版本的一個幾乎等價的結果。

　　唯一的區別是每條從節點 $x\left(v_{p}^{0}\right)$ 到 $y\left(v_{p}^{k}\right)$ 隨機行走的路徑 $v_{p}^{0}, v_{p}^{1}, \ldots, v_{p}^{k}$ 概率不是 $\rho \prod_{l=1}^{k} \frac{1}{\overline{\operatorname{deg}\left(v_{p}^{l}\right)}}$ ，而是 $\frac{\rho}{Q} \prod_{l=1}^{k-1} \frac{1}{\widetilde{\operatorname{deg}\left(v_{p}^{l}\right)}} \cdot(\widetilde{\operatorname{deg}}(x) \widetilde{\operatorname{deg}}(y))^{-1 / 2}$，其中 $Q$ 是歸一化因數。因此，概率上的差異很小，特別是當 $x$ 和 $y$ 的度很接近時。

　　同樣地，我們可以證明具有方向性偏差的鄰域聚集方案類似於有偏的隨機遊動分布。然後將相應的概率代入定理1的證明中。

　　根據經驗，我們觀察到，儘管有些簡化的假設，我們的理論是接近於在實踐中發生的事情。我們將訓練過的gcn的一個節點（標記為平方）的影響分布的熱圖可視化，並與從同一節點開始的隨機遊動分布進行比較。Figure 2 顯示了示例結果。

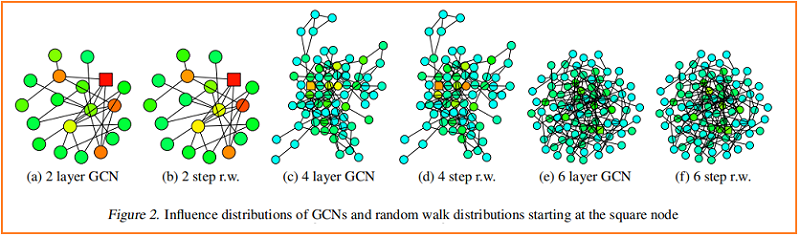
　　較深的顏色對應著較高的影響概率。為了顯示跳過連接的效果，Figure 3 可視化了一個類似的熱圖——具有 residual connections 的 GCN。事實上，我們觀察到，具有殘差連接的網路的影響分布近似對應於惰性隨機遊動：每一步都有更高的概率停留在當前節點上。在每次迭代中，所有節點都以相似的概率保留局部資訊；這不能適應特定上層節點的不同需求。

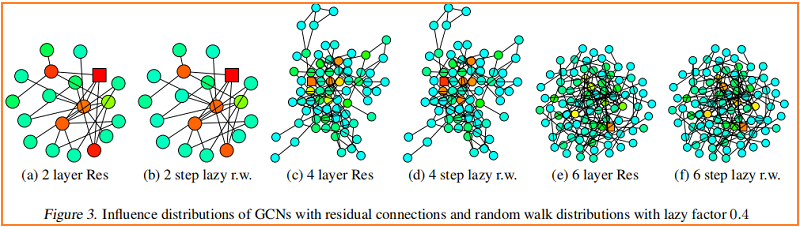
Fast Collapse on Expanders

　　從圖中心開始的隨機遊走能在 $O(\log |V|)$ 步驟中迅速收斂到一個幾乎均勻的分布。在鄰域聚合的 $O(\log |V|)$ 迭代之後，通過 Theorem 1，每個節點的表示幾乎受到圖內部中任何其他節點的影響。因此，節點表示將代表全局圖，並攜帶關於單個節點的有限資訊。

　　相比之下，從 bounded tree-width 部分開始的隨機遊動收斂緩慢，即這些特徵保留了更多的局部資訊。施加固定隨機遊動分布的模型繼承了這些擴展速度上的差異，並影響了鄰域，這可能不會導致對所有節點的最佳表示

5 Jumping Knowledge Networks

　　大半徑可能導致過多的平均，而小半徑可能導致不穩定或資訊聚集不足。因此，我們提出了兩個簡單而強大的架構變化——jump connection 和 subsequent selective 但自適應的聚合機制。

　　Figure 4 說明了主要的思想：在常見的鄰域聚合網路中，每一層都通過聚集前一層的鄰域來增加影響分布的大小。在最後一層，對於每個節點，我們仔細地從所有這些迭代表示（它們「跳轉」到最後一層）中選擇，潛在地結合一些。如果這是對每個節點獨立完成的，那麼該模型就可以根據需要調整每個節點的有效鄰域大小，從而完全得到所需的自適應能力。

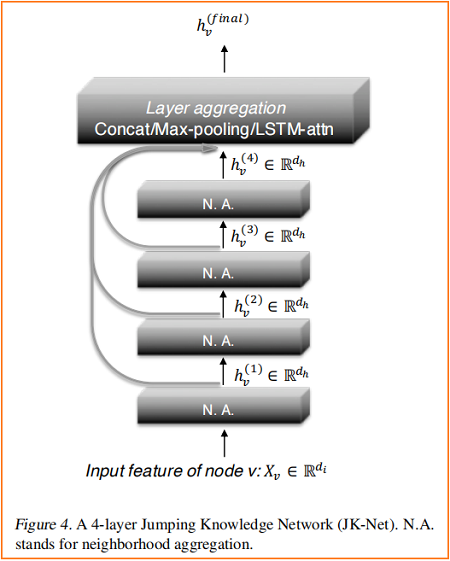
　　我們的模型允許一般的圖層聚合機制。我們探索了三種方法；其他的也是可能的。設 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$ 是要聚合的節點 $v$ (來自 $k$ 個層)的跳躍表示。

Concatenation

　　直接拼接 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$是組合各層的最直接的方法，之後可以進行線性變換。如果轉換權值在圖節點之間共享，那麼這種方法就不是節點自適應的。相反，它優化權重，以最適合數據集的方式組合子圖特徵。人們可能會認為連接適合於小圖和具有規則結構、自適應性較少的圖；也因為權重共享有助於減少過擬合。

　　$\max \left(h_{v}^{(1)}, \ldots, h_{v}^{(k)}\right)$ 選擇最具資訊的特徵。例如，表示更多局部屬性的特徵坐標可以使用從近鄰學習到的特徵坐標，而那些表示全局狀態的特徵坐標將有利於來自更高層的特徵。最大池化是自適應的，其優點是不引入任何額外的參數來學習。

LSTM-attention

　　注意機制通過計算每一層 $l\left(\sum_{l} s_{v}^{(l)}=1\right)$ 的注意分數 $s_{v}^{(l)}$ 來識別每個節點 $v$ 最有用的鄰域範圍，這代表了節點 $v$ 在第 $l$ 層學習到的特徵的重要性。節點 $v$ 的聚合表示是層特徵 $\sum_{l} s_{v}^{(l)} \cdot h_{v}^{(l)}$ 的加權平均值。對於 LSTM 的注意力，我們輸入 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$ 到 bi-directional LSTM ，並為每一層 $l$ 生成 forward-LSTM 和 backward-LSTM 隱藏特徵 $f_{v}^{(l)}$ 和 $b_{v}^{(l)}$。連接特徵的線性映射 $\left[f_{v}^{(l)} \| b_{v}^{(l)}\right]$ 產生標量重要性分數 $s_{v}^{(l)}$。對 $\left\{s_{v}^{(l)}\right\}_{l=1}^{k} $ 應用 Softmax 層使節點 $v$ 在不同範圍內對其鄰域的關注。使節點 $v$ 在不同範圍內對其鄰域的關注。最後，我們取 $\left[f_{v}^{(l)} \| b_{v}^{(l)}\right]$ 的和，用 $SoftMax  \left(\left\{s_{v}^{(l)}\right\}_{l=1}^{k}\right)$ 加權，得到最終的層表示。另一種可能的實現是將 LSTM 與 max-pooling 結合起來。LSTM-attention 是節點自適應的，因為每個節點的注意分數是不同的。我們將看到，這種方法在大型複雜圖上閃耀，儘管由於它相對較高的複雜性，它可能在小圖（較少的訓練節點）上過擬合。

6 Experiments

數據集

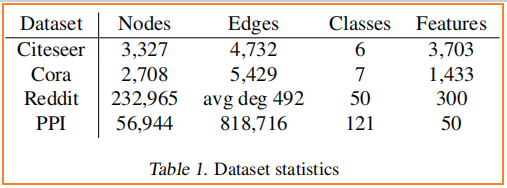
節點分類

7 Conclusion