論文解讀(MaskGAE)《MaskGAE: Masked Graph Modeling Meets Graph Autoencoders》
論文資訊
論文標題:MaskGAE: Masked Graph Modeling Meets Graph Autoencoders
論文作者:Jintang Li, Ruofan Wu, Wangbin Sun, Liang Chen, Sheng Tian……
論文來源:2022,arXiv
論文地址:download
論文程式碼:download
1 Introduction
MAE 在圖上的應用——2022 最潮的方法。
2 Related work and Motivation
2.1 GAE
GAEs採用了經典的編碼器-解碼器框架,旨在通過優化以下二進位交叉熵損失,從編碼圖的低維表示中進行解碼:
$\mathcal{L}_{\mathrm{GAEs}}=-\left(\frac{1}{\left|\mathcal{E}^{+}\right|} \sum\limits _{(u, v) \in \mathcal{E}^{+}} \log h_{\omega}\left(z_{u}, z_{v}\right)+\frac{1}{\left|\mathcal{E}^{-}\right|} \sum\limits _{\left(u^{\prime}, v^{\prime}\right) \in \mathcal{E}^{-}} \log \left(1-h_{\omega}\left(z_{u^{\prime}}, z_{v^{\prime}}\right)\right)\right)$
其中,$\mathcal{z}$ 代表低維隱表示,$f_{\theta}$ 代表參數為 $\theta$ 的 GNN encoder,$h_{\omega}$ 代表參數為 $\omega$ 的 GNN decoder,$\mathcal{E}^{+}$ 代表 positive edges ,$\mathcal{E}^{-}$ 代表 negative edges 。
2.2 Motivation
按照互資訊的思想:希望最大化 k-hop 節點對子圖之間的一致性,但是伴隨著 $K$ 值變大,過平滑的問題越發明顯,此時子圖大小對節點表示的學習不利。因此有:

分析了一堆廢話…………….
後面呢,必然出現解決過平滑的策略。
Recall:解決過平湖的策略
-
- 殘差;
- 譜圖理論;
- 多尺度資訊;
- 邊刪除;
3 Method:MaskGAE
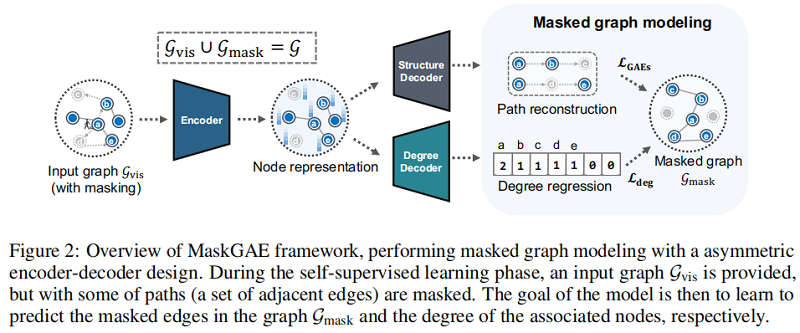
出發點:MGM
$\mathcal{G}_{\text {mask }} \cup \mathcal{G}_{\text {vis }}=\mathcal{G}$
$\mathcal{G}_{\text {mask }}= \left(\mathcal{E}_{\text {mask }}, \mathcal{V}\right)$
3.1 Masking strategy
Edge-wise random masking $(\mathcal{T}_{\text {edge }}$
$\mathcal{E}_{\text {mask }} \sim \operatorname{Bernoulli}(p)$
Path-wise random masking $(\mathcal{T}_{\text {path}}$
$\mathcal{E}_{\text {mask }} \sim \operatorname{Random} \operatorname{Walk}\left(\mathcal{R}, n_{\text {walk }}, l_{\text {walk }}\right)$
其中,$\mathcal{R} \subseteq \mathcal{V}$ 是從圖中取樣的一組根節點,$n_{\text {walk }}$ 為每個節點的行走次數,$l_{\text {walk }}$ 為行走長度。
在這裡,我們遵循度分布,抽樣了一個節點的子集(例如,50%),沒有替換作為根節點 $\mathcal{R}$。這樣的取樣也可以防止圖中存在的潛在的長尾偏差(即,更多的屏蔽邊是那些屬於高度節點的邊)。
3.2 Encoder
- GCN Encoder
- SAGE Encoder
- GAT Encoder
3.2 Decoder
$h_{\omega}\left(z_{i}, z_{j}\right)=\operatorname{Sigmoid}\left(z_{i}^{\mathrm{T}} z_{j}\right)$
$h_{\omega}\left(z_{i}, z_{j}\right)=\operatorname{Sigmoid}\left(\operatorname{MLP}\left(z_{i} \circ z_{j}\right)\right)$
$g_{\phi}\left(z_{v}\right)=\operatorname{MLP}\left(z_{v}\right)$
3.3 Learning objective
損失函數包括:
-
- Reconstruction loss:計算的是掩碼邊 $\mathcal{E}^{+}=\mathcal{E}_{\text {mask }}$ 的重構損失;
- Regression loss:衡量的是節點度的預測與掩蔽圖中原始節點度的匹配程度:
$\mathcal{L}_{\mathrm{deg}}=\frac{1}{|\mathcal{V}|} \sum\limits _{v \in \mathcal{V}}\left\|g_{\phi}\left(z_{v}\right)-\operatorname{deg}_{\text {mask }}(v)\right\|_{F}^{2}$
因此,總體損失為:
$\mathcal{L}=\mathcal{L}_{\mathrm{GAEs}}+\alpha \mathcal{L}_{\mathrm{deg}}$
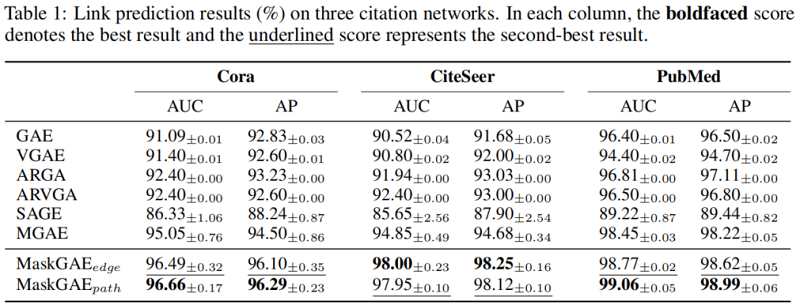
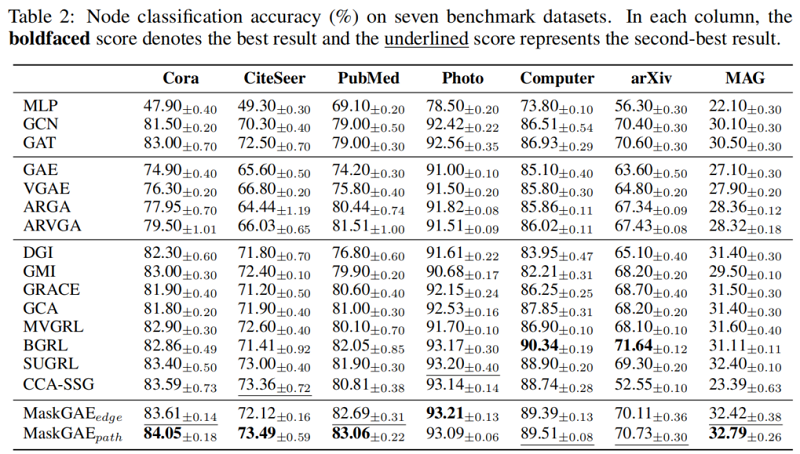
4 Experiments