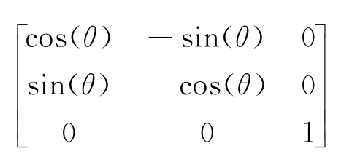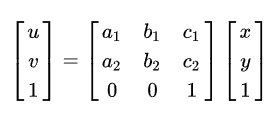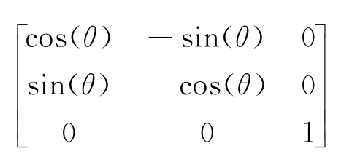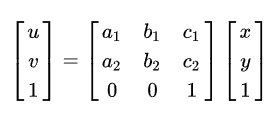[原創]一種自動化九點標定工具原理（包涵部分源碼）

• 2022 年 7 月 21 日
• 筆記
• 自動化

1. 什麼是標定？

• 工業應用中相機拍到一個mark點的坐標為C1（Cx,Cy），C1點對應的龍門架/機械手等執行端對應的坐標是多少？
• 標定就是解決這個問題，如相機拍到一個點坐標C1（Cx,Cy），通過標定公式的計算得到點R1（Rx,Ry），R1就是龍門架/機械手坐標系的真實點位
• C1與R1之間存在一種固定的關係，求解這個關係的過程叫做標定

2. 為什麼是9點標定？

• C1與R1之間的關係只有三種平移、縮放、旋轉
• 矩陣中有對三種關係的公式如下：
• 平移矩陣公式
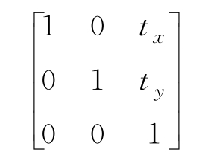
• 縮放矩陣公式
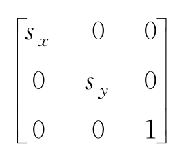
• 旋轉矩陣公式
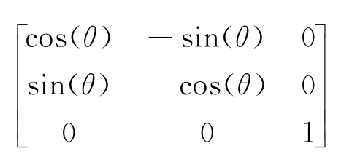
• 上面三種矩陣相乘合成一個矩陣就是仿射變換矩陣
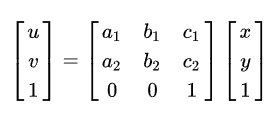
• 最後一個矩陣是根據前3個矩陣相乘得到，故為得到最終的放射變換矩陣，需要知道 Tx，Ty，Sx，Sy，θ這5個參數。為得到5個參數至少需要5個不同等式。
• 故此我們得出結論最少5個點我們就可以推到出最終的放射變換矩陣。
• 那為什麼是9點標定呢？答案是為了提高精度，通過9個點我們可以有N種組合算出結果，基於這些結果我們求類似於平均值的東西提高精度
• 那為什麼不是10個，11個或更多點呢？答案是9個點的計算已經基本滿足大家對精度的要求了，如π=3.1415926已經滿足計算精度了，就沒必要再把π計算到小數點後100位了

3. 怎麼實現9點標定呢？

• 拿到9個相機點位[C1,C2…C9],同時拿到這9個點對應的機械手或龍門架真實坐標[R1,R2…R9]
• 把上面數據套入halcon的vector_to_hom_mat2d運算元，就可以得到放射變換矩陣了

*像素坐標
Row1:=[1,2,3,4,5,6,1,2,3,4,5,6,1,2,3,4,5,6]
Column1:=[1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3]

*機械坐標
Row2:=[50,51.999,54.999,56.999,59.999,62.996,-4.999,-3,0,1.999,4.999,7.995,-59.998,-57.001,-55.001,-52.001,-49.003,-45.005]
Column2:=[-93.3,-47.299,0.002,45.499,91.498,135.493,-92.301,-44.3,0,46.999,91.497,135.494,-90.297,-44.297,1.003,46.999,91.497,134.494]

*求解放射變換矩陣
vector_to_hom_mat2d (Row1, Column1, Row2, Column2, HomMat2D)

*保存變換矩陣到HomMat2D.mat中
serialize_hom_mat2d (HomMat2D, SerializedItemHandle)
open_file ('HomMat2D.mat', 'output_binary', FileHandle) 
fwrite_serialized_item (FileHandle, SerializedItemHandle) 
close_file (FileHandle)

4. 傳統的9點標定工具怎麼做？

• 求解9點工具的難點在於怎麼得到相機拍照點C1對應的真實坐標R1？
• 傳統的作法是在機械手或龍門架的執行端下掛一個針尖。讓龍門架/機械手到達標定板的點位1使針尖與點位1中心重合，記錄真實位置，同時通過拍照得出點位1的相機坐標

5. 還有沒有更方便的9點標定工具？其原理是什麼？

• 有，其核心原理是取消針尖，通過旋轉180度方式求解出相機坐標點C1
• 如機械手在物理點位R1（Rx，Ry）拍照的到此mark點對應的相機坐標C1（Cx1，Cy1），然後讓機械手旋轉180度再次拍照的到mark點對應相機坐標C2（Cx2，Cy2）。那麼物理點R1（Rx，Ry）對應的相機的點位未C1,C2的中心點。 因為物料點圍繞自己旋轉真實點位並未發生變化。
• 通過這種方法就可以實現自動化的9點標定工具

6. 此工具適用範圍

• 此工具只適用於固定相機（眼在手外）的標定，如底部相機，頂部固定相機。
• 對於相機隨龍門架/機械手移動（眼在手上）的標定請聽下回分解

7. 源碼

         private Position updatePoiMatrix(Position pcbPoi, Position dstPoi)
        {
            //到上一個放pcb的點位
            this.currentRobot.GoToPosition(pcbPoi);
            this.currentCylinder.Open();
            //到達待測量的點位
            this.currentRobot.GoToPosition(dstPoi);
            this.currentRobot.GoToPosition(dstPoi);
            //放板
            this.currentCylinder.Close();
            Thread.Sleep(600);
            Position pUp = dstPoi.Copy();
            pUp.Z = this.currentRobot.GetSafeZ();
            this.currentRobot.GoToPosition(pUp);
            //到達安全點位 
            this.currentRobot.GoToPosition(safePoi);
            //拍照獲取mark點
            Position poi1 = this.getMarkPoi();
            this.currentRobot.GoToPosition(dstPoi);
            //打開
            this.currentCylinder.Open();
            //先上升一定的高度再旋轉
            Position dstPoi2 = dstPoi.Copy();
            dstPoi2.Z = this.currentRobot.GetSafeZ();
            this.currentRobot.GoToPosition(dstPoi2);
            //旋轉180度
            if (dstPoi2.U > 90)
            {
                dstPoi2.U -= 180;
            }
            else if (dstPoi2.U < -90)
            {
                dstPoi2.U += 180;
            }
            else
            {
                dstPoi2.U += 180;
            }
            this.currentRobot.GoToPosition(dstPoi2);
            dstPoi2.Z = dstPoi.Z;
            this.currentRobot.GoToPosition(dstPoi2);
            //放板
            this.currentCylinder.Close();
            Thread.Sleep(600);
            //到達安全點位 
            this.currentRobot.GoToPosition(safePoi);
            //拍照獲取mark2點
            Position poi2 = this.getMarkPoi();
            //更新對應的數組
            imagePoiList.Add(new Position() { X = (poi1.X + poi2.X) / 2, Y = (poi1.Y + poi2.Y) / 2 });
            robotPoiList.Add(dstPoi2.Copy());
            //返回取PCB的最新位置
            return dstPoi2;
        }
         public void SaveMat(List<Position> imageList, List<Position> robotPoiList, string path)
        {
            HTuple imageXList = new HTuple(), imageYList = new HTuple();
            HTuple robotXList = new HTuple(), robotYList = new HTuple();

            for (int i = 0; i < imageList.Count; i++)
            {
                imageXList[i] = imageList[i].X;
                imageYList[i] = imageList[i].Y;
                robotXList[i] = robotPoiList[i].X;
                robotYList[i] = robotPoiList[i].Y;
            }

            HTuple hv_HomMat2D = new HTuple(), hv_SerializedItemHandle = new HTuple();
            HTuple hv_FileHandle = new HTuple();
            ////標定
            hv_HomMat2D.Dispose();
            HOperatorSet.VectorToHomMat2d(imageXList, imageYList, robotXList, robotYList, out hv_HomMat2D);

            //保存變換矩陣
            hv_SerializedItemHandle.Dispose();
            HOperatorSet.SerializeHomMat2d(hv_HomMat2D, out hv_SerializedItemHandle);
            hv_FileHandle.Dispose();
            HOperatorSet.OpenFile(path, "output_binary", out hv_FileHandle);
            HOperatorSet.FwriteSerializedItem(hv_FileHandle, hv_SerializedItemHandle);
            HOperatorSet.CloseFile(hv_FileHandle);

            imageXList.Dispose();
            imageYList.Dispose();
            robotXList.Dispose();
            robotYList.Dispose();
            hv_HomMat2D.Dispose();
            hv_SerializedItemHandle.Dispose();
            hv_FileHandle.Dispose();
        }