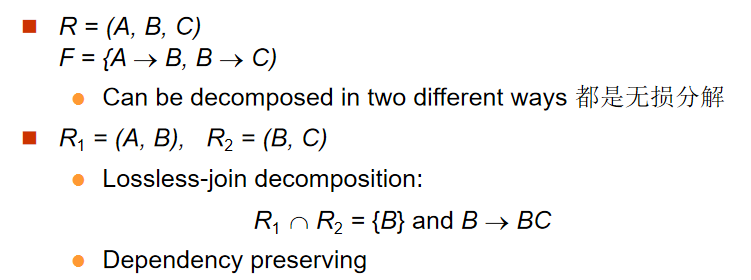資料庫系統原理「通關指南」
資料庫概述(Introduction)
什麼是資料庫管理系統
Database Management System (DBMS)- 數據 + 管理系統
資料庫存在的價值
Data redundancy and inconsistency(冗餘與不一致性)Difficulty in accessing data(獲取數據困難)Data isolation(數據孤島)Integrity problems(完整性問題)
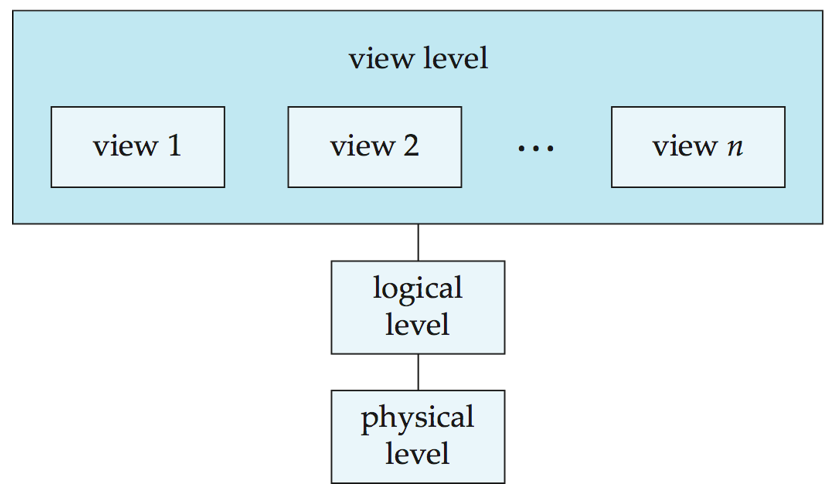
資料庫的三層抽象
- 物理層(
Physical level):最低層次的抽象,描述數據實際上是怎樣存儲的。物理層詳細描述複雜的底層數據結構。 - 邏輯層(
Logical level):比物理層層次稍高的抽象,描述資料庫中存儲什麼數據及這些數據間存在什麼關係。這樣邏輯層就通過少量相對簡單的結構描述了整個資料庫。雖然邏輯層的簡單結構的實現可能涉及複雜的物理層結構,但邏輯層的用戶不必知道這樣的複雜性。這稱作物理數據獨立性(physical data independence)。資料庫管理員(DBA)使用抽象的邏輯層,他必須確定資料庫中應該保存哪些資訊。 - 視圖層(
View level):視圖層(view level)。最高層次的抽象,只描述整個資料庫的某個部分。儘管在邏輯層使用了比較簡單的結構,但由於一個大型資料庫中所存資訊的多樣性,仍存在一定程度的複雜性。資料庫系統的很多用戶並不需要關心所有的資訊,而只需要訪問資料庫的一部分。視圖層抽象的定義正是為了使這樣的用戶與系統的交互更簡單。系統可以為同一資料庫提供多個視圖。
實例與模式
-
實例(Instances):指特定時刻存儲在資料庫中的資訊的集合
-
模式(Schemas):指資料庫的總體設計
- 物理模式(physical schemas):在物理層描述資料庫的設計
- 邏輯模式(logical schemas):在邏輯層描述資料庫的設計。程式設計師使用邏輯模式來構造資料庫應用程式
- 子模式(subschemas):描述了資料庫的不同視圖
數據模型(Data model)
- 關係模型(retional model):用表的集合來表示數據和數據間的聯繫
- 實體-聯繫模型(entity-relationship model):基於對現實世界的認識——現實世界由一組稱作實體的基本對象以及這些對象間的聯繫構成。廣泛用於資料庫設計
- 基於對象的數據模型(object-based data model):基於面向對象設計思想
- 半結構化數據模型(semistructured data model):可拓展標記語言
xml,eXtensible,Markup,Language
資料庫構成(Database System Internals)

資料庫架構(Database Architecture)
Centralized(集中式)Client-server(客戶/伺服器式)Parallel (multi-processor)(並行)Distributed(分散式)
關係型資料庫概述( Intro to Relational Model)
關係 (Relation)
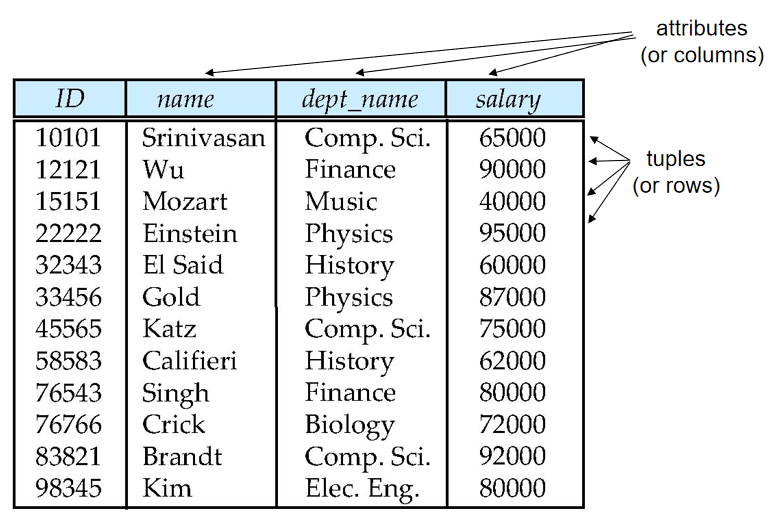
- 屬性(attributes):表中每一列數據。
A1, A2, …, An - 元組(tuples):表中每一行數據
- 關係(relation):關係是無序的
- 關係實例(relation instance):表
- 關係模式(relation schema):
R = (A1, A2, …, An )。例如:instructor = (ID, name, dept_name, salary)
碼/鍵(keys)
-
超碼(super key):一個或一組屬性,能夠唯一區分一個關係的任何一個元組。例如
{ID, name},{ID} -
候選碼(candidate key):最小的(包含屬性個數最少)超碼。例如
{ID} -
主碼(primary key):候選碼中挑出一個作為主碼,任何關係只能有一個主碼
-
外碼(foreign key):一個表中某一列的所有值一定出現在另一張表的某一列,且在另一張表中為主碼
大學資料庫模式圖
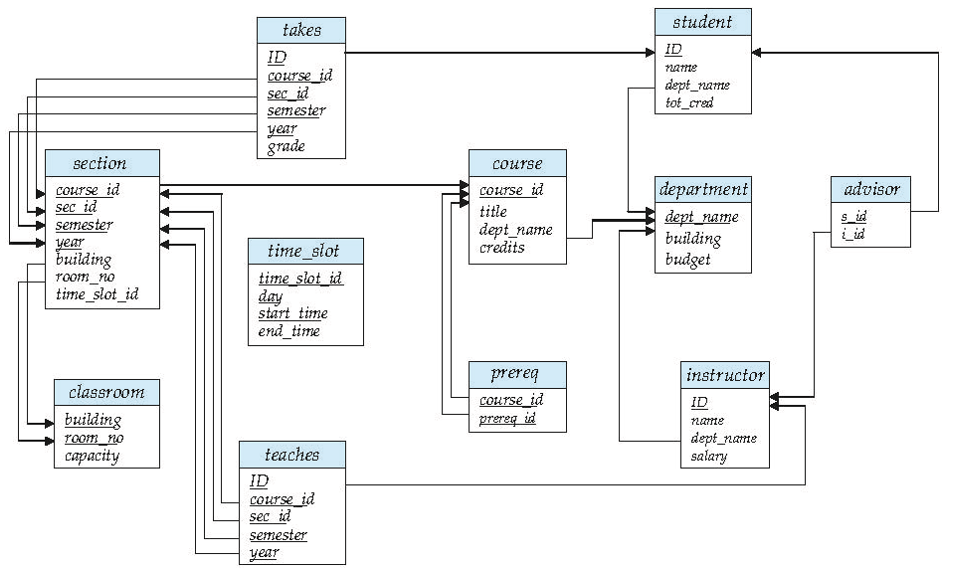
department(dept_name,building,budget);
instructor(ID, name,dept_name,salary);
course(course_id,title,dept_name,credits);
section(course_id,sec_id,semester,year,building,room_number,time_slot_id);
teaches(ID,course_id,section_id,semester,year);
student(ID,name,dept_name,tot_cred);
prereq(course_id,prereq_id);
Advisor(s_id,i_id)
takes(ID,course_id,sec_id,semester,year,grade)
classroom(building,room_number,capacity)
time_slot(time_slot_id,day,start_time,end_time)
大學資料庫 E-R 圖
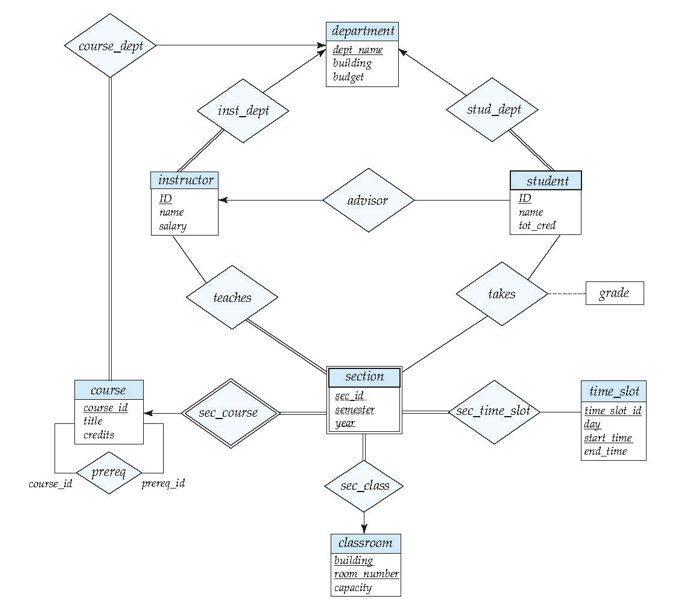
形式化關係查詢語言( Formal Relational Query Languages )
關係代數(Relational Algebra)
1️⃣ 選擇(Select Operation)
-
定義:$ \sigma _p (r)$ = {t | t $ \in $ r and p(t)},p 是謂詞,選擇出滿足謂詞的元組
-
例題:
- 選出物理系或者年薪資大於70000美元的老師:$ \sigma _{dept_name=”Physics” \lor ,,salary>70000}\left( instructor \right) ,,$
- 選出除了物理和電腦學院之外的老師:$ \sigma _{dept_name\ne ”Physics” \land ,,depe_name\ne ”Comp.Sci.”}\left( instructor \right) $
2️⃣ 投影(Project Operation)
-
定義:$ \prod\nolimits_{A_1,A_2,…,A_k}^{}{\left( r \right)}$,選出特定的屬性,結果只包含這 k 列,其他列不顯示
-
例題:
- 找出所有電腦學院的老師的姓名:$ \prod\nolimits_{name}^{}{\left( \sigma _{\mathrm{de}pt_name=”Comp.Sci.”}\left( instructor \right) \right)}$
3️⃣ 集合併(Union Operation)
-
定義: r $ \cup $ s = {t | t $\in $ r or t $ \in $ s},兩表查詢結果合併
-
要點:
r,s必須包含相同屬性,即同元r,s屬性的域必須相容
-
例題:
-
找出所有在 2018 年秋季或者在 2019 年春季開課的課程:
\[\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=”Fall” \land \,\,year=2018}\left( \sec tion \right) \right) \cup}\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=”Spring” \land \,\,year=2019}\left( \sec tion \right) \right)}
\]
-
4️⃣ 集合差(Set Difference Operation)
-
定義:r – s = {t | t $ \in $ r and t \(\notin\) s},查詢出屬於
r但不屬於s的元組 -
要點:
r,s必須包含相同屬性,即同元r,s屬性的域必須相容
-
例題:
-
找出所有在 2018 年秋季但不在 2019 年春季開課的課程:
\[\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=”Fall”\land \,\,year=2018}\left( \sec tion \right) \right) -}\prod\nolimits_{course\_id}^{}{\left( \sigma _{semester=”Spring”\land \,\,year=2019}\left( \sec tion \right) \right)}
\]
-
5️⃣ 笛卡爾積(Cartesian-Product Operation)
-
定義:r $ \times $ s = {t q | t $ \in $ r and q $ \in $ s}
-
要點:
- 笛卡爾積之後形成的新表要改名
- 注意兩表中相同屬性命名使用
表名.屬性名或其別名
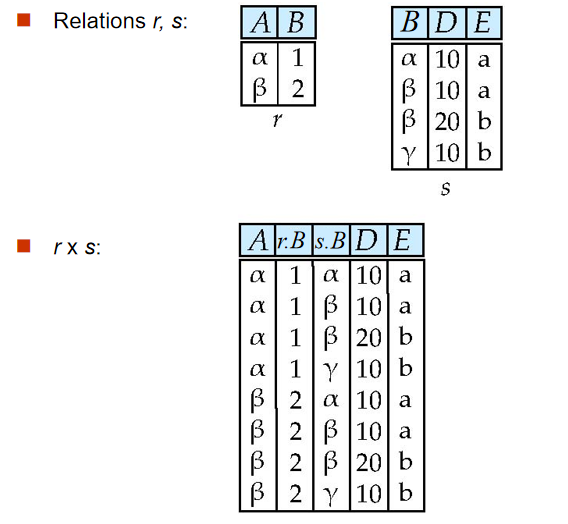
-
例題:
-
選出電腦學院所有學生的選課資訊
先笛卡爾積再選擇:$ \sigma _{dept_name=’Comp.Sci.’}\left( \sigma _{student.ID=takes.ID}\left( student\times takes \right) \right) $
先選擇在笛卡爾積:$ \sigma _{student.ID=takes.ID}\left( \sigma _{dept_name=’Comp.Sci.’}\left( student \right) \times takes \right) $
-
6️⃣ 更名(Rename Operation)
- 定義:$ \rho _{x\left( A_1,A_2,…,A_n \right)}\left( E \right) $,對於表
E,重命名為x,投影屬性重命名為 $ A_1,A_2,…,A_n $
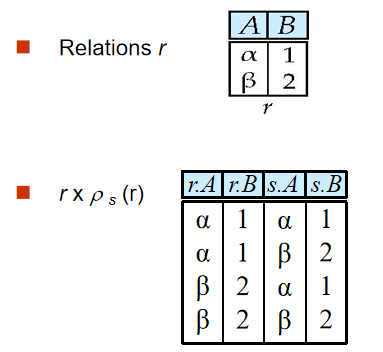
關係代數表達式
-
定義:把關係或常數關係通過關係代數連接起來形成的表達式
-
例題:
-
找出選了教師Einstein所教課程的所有學生的 ID,注意結果不能重複.
$ \prod\nolimits_{ta.ID}^{}{\left( \sigma _{te.course_id=ta.course_id\land te.\sec tion_id=ta.section_id\land te.semester=ta.semester\land te.year=ta.year}\left( \sigma _{i.ID=te.ID\land name=’Eisntein’}\left( \rho _i\left( instructor \right) \times \rho _{te}\left( teaches \right) \times \rho _{ta}\left( takes \right) \right) \right) \right)}$
-
查出大學裡的最高工資
$ \prod\nolimits_{salary}^{}{\left( instructor \right) -\prod\nolimits_{instructor.salary}^{}{\left( \sigma _{instructor.salary<d.salary}\left( instructor\times \rho _d\left( instructor \right) \right) \right)}}$
-
附加關係代數(Additional Operations)
1️⃣ 集合交(Set-Intersection Operation)
-
定義: r $ \cap $ s = {t | t $\in $ r and t $ \in $ s}
-
要點:
r,s必須包含相同屬性,即同元r,s屬性的域必須相容
-
注意:$ r\cap s=r-\left( r-s \right) $

2️⃣ 除法(Division Operation)
- 定義:$ r\div s $
- $ R=\left( A_1,A_2,…A_m,B_1,B_2,…B_n \right) ,S=\left( B_1,B_2,…B_n \right)$
- 解釋:前提是
s表的屬性包含於r表。則r表屬性去掉s表的屬性之後,r表中包含s表所有數據的元組被選出。其實文字比較難以形容,看圖理解更好。
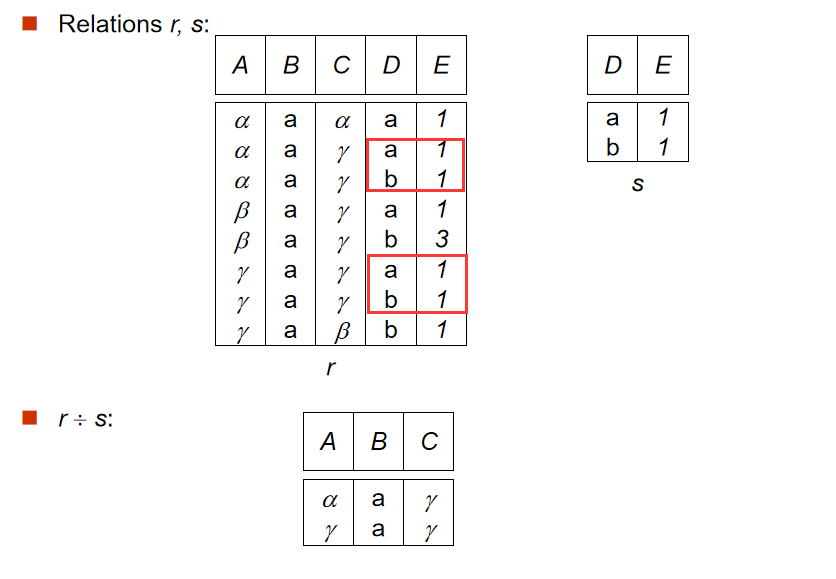
-
應用:帶有「包含某某集合所有元素」的問題,可以使用除法解決
-
例題:
- 選出選了電腦系所有課程的學生的 ID:$ \prod\nolimits_{course_id,ID}^{}{\left( takes \right) \div \left( \prod\nolimits_{course_id}^{}{\left( \sigma _{department=’Comp.Sci.’}\left( course \right) \right)} \right)}$
3️⃣ 賦值(Assignment Operation)
- 定義:$ temp\gets expression $,查詢結果保存在臨時表
4️⃣ 自然連接(Natural Join Operation)
- 定義:$ r\Join s $,
r表和s表根據重複屬性進行笛卡爾積,最後去除重複屬性
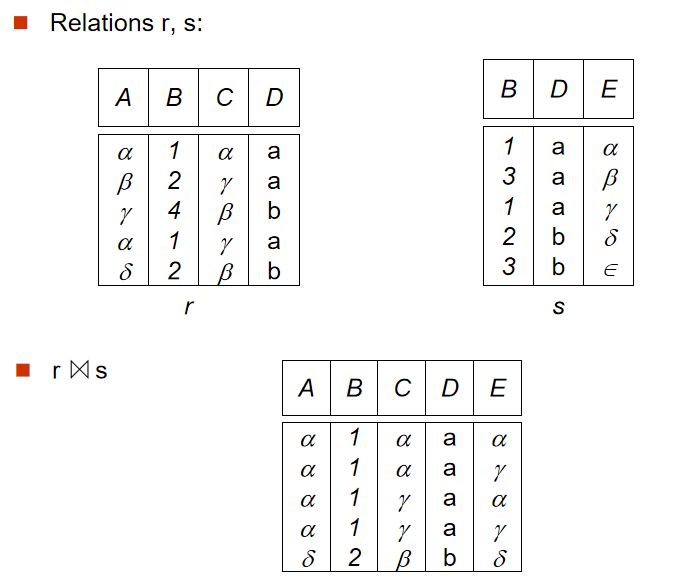
-
例題:
-
查找電腦學院所有老師的名字以及他們所上課程的名字
$ \prod\nolimits_{name,title}^{}{\left( \sigma _{dept_name=’Comp.Sci.’}\left( instructor\Join teaches\Join course \right) \right)}$
-
查找教授 『D.B.S’ 和 』O.S『 的老師的名字以及課程名稱
$ \prod\nolimits_{name,title}^{}{\left( instructor\Join teaches\Join course \right) } $ \(\div \rho _{title}\left( temp \right) \left( \left\{ \left( ”D.B.S” \right) ,\left( ”O.S” \right) \right\} \right)\)
-
拓展關係代數(Extended Relational-Algebra-Operations)
1️⃣ 廣義投影(Generalized Projection)
-
定義:$ \prod\nolimits_{F_1,F_2,…F_n}^{}{\left( E \right)}$
-
解釋:投影可以進行四則運算
-
舉例:$ \prod\nolimits_{customer,limit-balance}^{}{\left( credit \right)}$
2️⃣ 聚集函數(Aggregate Functions and Operations)
-
定義:
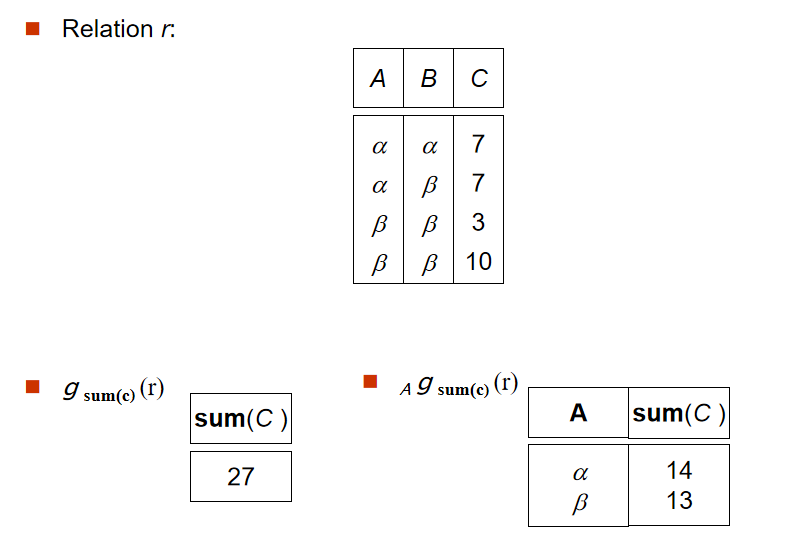
\[_{G_1,G_2,…,G_n}g_{F_1\left( A_1 \right) ,F_2\left( A_2 \right) ,…,F_n\left( A_n \right)}\left( E \right)
\] -
解釋:
G:選中進行分組的屬性(可以為空)F:聚集函數(sum,avg,min,max,count)A:聚集函數作用的屬性
-
要點:
- 除了
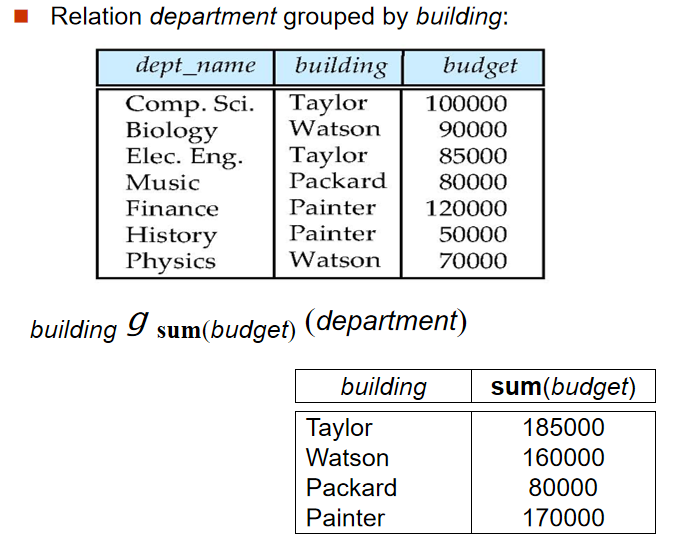
count(*)會保留null,對所有行進行統計,其他聚集函數會忽視值為null的屬性 - 可對聚集之後的屬性進行更名操作:
\[_{building}g_{sum\left( budget \right) \,\,as\,\,sum\_budget}\left( department \right)
\]
- 除了
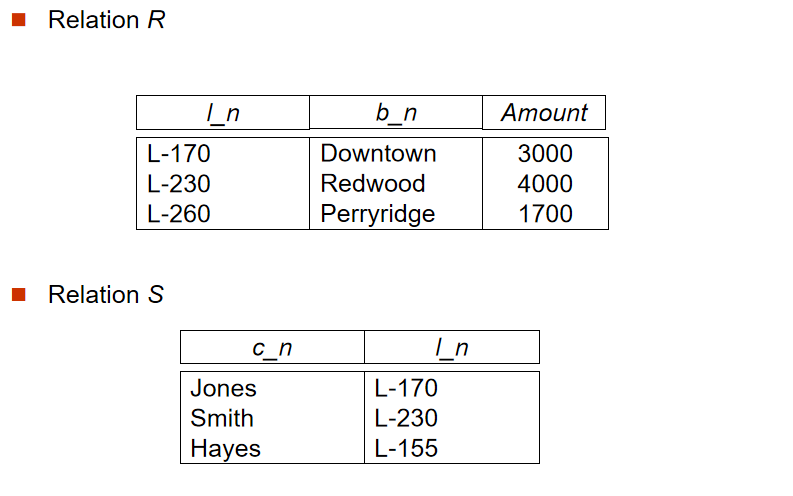
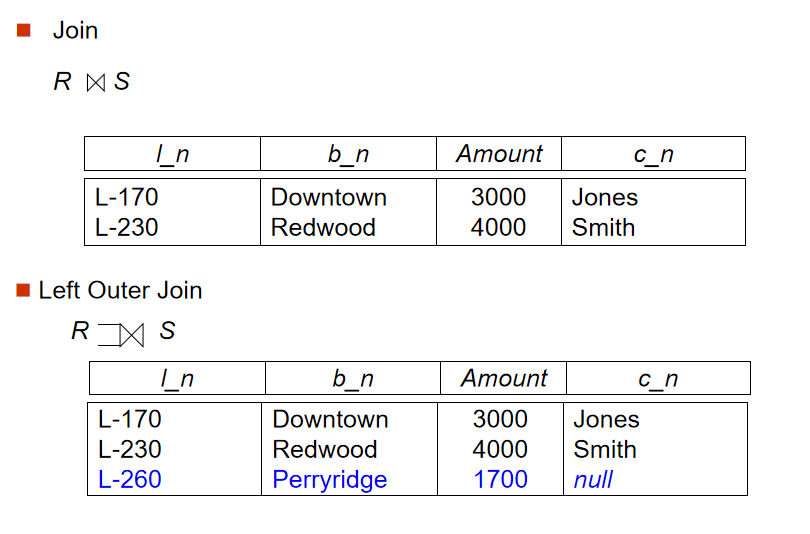
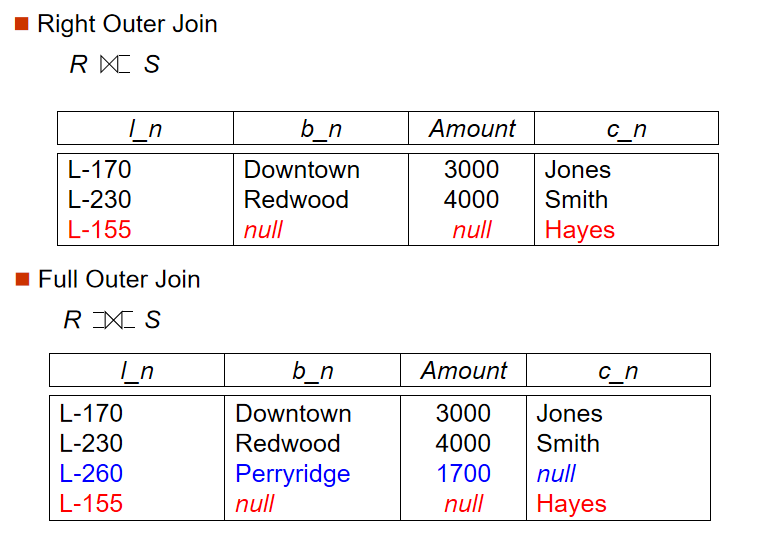
3️⃣ 外連接(Outer Join)
-
定義:保留連接過程中某表的所有數據,連接操作的延申,能避免資訊的丟失
-
左外連接(左表完整),右外連接(右表完整),全外連接(左右表完整)
NULL值問題
-
定義:
null表示一個不確定(unknown)的值,或一個不存在的值 -
unknown的邏輯運算:優先順序上false < unknown < true# OR unknown or true = true unknown or false = unknown unknown or unknown = unknown # AND unknown and true = unknown unknown and false = false unknown and unknown = unknown # NOT not unknown = unknown
修改關係代數(Modification of the Database)
1️⃣ 刪除(Deletion)
-
定義:$ r\gets r-E $
-
解釋:可以刪除整條元組,但不可以刪除某些屬性
-
例題:
- 刪除所有物理學院的老師:$ instructor\gets instructor-\sigma _{dept_name=’Physics’}\left( instructor \right) $
2️⃣ 插入(Insertion)
-
定義:$ r\gets r\cup E $
-
解釋:
r表並上查詢結果E,賦值給r表 -
例題:
-
插入
instrutor表,ID 為 1111,教師”Peter”,年薪 72000:\[instructor\gets instructor\cup \left\{ \left( ”1111”,”Peter”,,72000 \right) \right\}
\]\[instructor\gets instructor\cup \left\{ \left( ”1111”,”Peter”,null,72000 \right) \right\}
\]
-
3️⃣ 更新(Updating)
-
定義:$ r\gets \prod\nolimits_{F_1,F_2,…F_I}^{}{(r)} $
-
解釋:可以改變某個元組當中的某個值。
-
例題:
- 所有老師年薪提高百分之五:$ instructor\gets \prod\nolimits_{id,name,dept_name,salary*1.05}^{}{\left( instructor \right)}$
結構化查詢語言 SQL
SQL 語言在功能上主要分為如下3大類:
DDL(Data Definition Language、數據定義語言),這些語句定義了不同的資料庫、表、視圖、索引等資料庫對象,還可以用來創建、刪除、修改資料庫和數據表的結構。主要的語句關鍵字包括 CREATE 、 DROP 、 ALTER 等。
DML(Data Manipulation Language、數據操作語言),用於添加、刪除、更新和查詢資料庫記錄,並檢查數據完整性。主要的語句關鍵字包括 INSERT 、 DELETE 、 UPDATE 、 SELECT 等。SELECT是 SQL 語言的基礎,最為重要。
DCL(Data Control Language、數據控制語言),用於定義資料庫、表、欄位、用戶的訪問許可權和安全級別。主要的語句關鍵字包括 GRANT 、 REVOKE 、 COMMIT 、 ROLLBACK 、 SAVEPOINT 等
DQL(Data Query Language、數據查詢語言),有時單獨把 SELECT 拿出來作為 DQL 分類
DDL(Data Definition Language)
常用資料庫數據類型

VARCHAR vs CHAR
CHAR 和 VARCHAR 類型都可以存儲比較短的字元串。
CHAR類型CHAR(M)類型一般需要預先定義字元串長度。如果不指定(M),則表示長度默認是1個字元。- 如果保存時,數據的實際長度比
CHAR類型聲明的長度小,則會在右側填充空格以達到指定的長度;如果數據的實際長度比CHAR類型聲明的長度大,則會截取前M個字元。當MySQL檢索CHAR類型的數據時,CHAR類型的欄位會去除尾部的空格。 - 🔔 定義
CHAR類型欄位時,聲明的欄位長度即為CHAR類型欄位所佔的存儲空間的位元組數。 - 🌋 固定長度;浪費存儲空間;效率高;適用於存儲不大,速度要求高的情況
VARCHAR類型VARCHAR(M)定義時, 必須指定長度M,否則報錯。MySQL4.0版本以下,varchar(20):指的是 20 位元組,如果存放UTF8漢字時,只能存 6 個(每個漢字 3 位元組);MySQL5.0版本以上,varchar(20):指的是 20 字元。- 🔔 檢索
VARCHAR類型的欄位數據時,會保留數據尾部的空格。VARCHAR類型的欄位所佔用的存儲空間為字元串實際長度加 1 個位元組。 - 🌋 可變長度;節省存儲空間;效率低;適合非
CHAR的情況
CLOB vs BLOB
-
CLOB類型- 將字元大對象 (Character Large Object) 存儲為資料庫表某一行中的一個列值,使用
CHAR來保存數據
- 將字元大對象 (Character Large Object) 存儲為資料庫表某一行中的一個列值,使用
-
BLOB類型- 可以存儲一個二進位的大對象(Binary Large Object),比如 圖片 、音頻和影片等
-
當查詢結果是個大對象時,返回的不是對象本身,而是一個定位器
約束
| 關鍵詞 | 名稱 |
|---|---|
PIRMARY KEY |
主鍵(唯一+非空) |
FOREIGN KEY |
外鍵 |
UNIQUE |
唯一約束 |
NOT NULL |
非空約束 |
CHECK(p) |
謂詞約束 |
INDEX |
普通索引 |
# PRIMARY KEY
## 創建(1)
CREATE TABLE name(
ID INT(11) PRIMARY KEY
);
## 創建(2)
CREATE TABLE name(
ID INT(11),
PRIMARY KEY(ID)
);
## 創建(3)
ALTER TABLE name ADD PRIMARY KEY(ID);
## 刪除
ALTER TABLE name DROP PRIMARY KEY;
# ——————————————————————————————————————————————————————————
# FOREIGN KEY
## 創建(1)
CREATE TABLE name(
ID INT(11),
FOREIGN KEY(ID) REFERENCES name2(ID)
);
## 創建(2)
ALTER TABLE name ADD CONSTRAINT fk_name_name1 FOREIGN KEY(ID) REFERENCES name2(ID);
## 刪除
ALTER TABLE name DROP FOREIGN KEY fk_name_name1;
# ———————————————————————————————————————————————————————————
# UNIQUE
## 創建(1)
CREATE TABLE name(
age INT UNIQUE
);
## 創建(2)
CREATE TABLE name(
age INT,
UNIQUE KEY(age)
);
## 創建(3)
ALTER TABLE name ADD CONSTRAINT uk_age UNIQUE KEY(age);
## 刪除
ALTER TABLE name DROP INDEX uk_age;
# ————————————————————————————————————————————————————————————
# NOT NULL
## 創建(1)
CREATE TABLE name(
age INT NOT NULL
);
## 創建(2)
ALTER TABLE name CHANGE COLUMN age age INT NOT NULL;
## 刪除
ALTER TABLE name CHANGE COLUMN age age INT NULL;
# ————————————————————————————————————————————————————————————
# CHECK(p)
## 創建(1)
CREATE TABLE name(
num INT CHECK(num > 0)
);
## 創建(2)
ALTER TABLE name ADD CONSTRAINT check_num CHECK(num > 0);
## 刪除
ALTER TABLE name DROP CONSTRAINT check_num;
# ————————————————————————————————————————————————————————————
# 創建普通索引 INDEX
## 創建(1)
CREATE TABLE name(
num INT,
INDEX [索引名](num)
);
## 創建(2)
CREATE INDEX 索引名 ON name(num);
## 創建(3)
ALTER TABLE name ADD INDEX 索引名(num);
## 刪除索引(1)
ALTER TABLE name DROP INDEX 索引名;
## 刪除索引(2)
DROP INDEX 索引名 ON name;
用戶自定義數據類型(User-Defined Types)
-
用戶對已有數據類型的特指和更名
-
MySQL不支援CREATE type 類型名 as 類型 # 例如:create type Dollars as numeric (12,2) final -
強類型檢查,只要自定義類型名字不同,數據類型就不同
域(Domains)
-
本質是可以帶約束的用戶自定義數據類型
-
MySQL不支援create domain 域名 類型 限制 # 例如:create domain person_name char(20) not null
DQL(Data Query Language)
SELECT [DISTINCT]FIELD1,FIELD2...
FROM TRABLE1[,TABLE2...]
[INNER]JOIN | LEFT [OUTER] JOIN | RIGHT [OUTER] JOIN | NATURAL JOIN TABLE3
ON 關聯條件... | USING(FIELD1,FIELD2...)
WHERE 查詢條件或子查詢
GROUP BY FIELD1,FIELD2...
HAVING 分組條件
ORDER BY FIELD1,FIELD2... [ASC][DESC]
UNION [ALL] 並上其他表的查詢結果
-
SELECT:查詢。 -
From:指明查詢的表,可以是實際存在的表,也可以是查詢產生的臨時表。 -
DISTINCT:對數據表中一個或多個欄位重複的數據進行過濾,只返回其中的一條數據給用戶,刪除重複數據。 -
[INNER]JOIN內連接,LEFT [OUTER] JOIN左外連接,LEFT [OUTER] JOIN右外連接,NATURAL JOIN自然連接,注意MySQL不支援全表連接FULL JOIN但是可以通過LEFT JOIN UNION RIGHT JOIN實現。 -
WHERE:指明查詢條件,可以沒有。 -
GROUP BY:分組 -
HAVING:分組後對每個組進行篩選,可以使用聚集函數(avg,sum...) -
ORDER BY:查詢結果排序,ASC升序,DESC降序 -
UNION [ALL]:合併多表查詢結果,默認去重,加ALL不去重
HAVING vs WHERE
HAVING:謂詞在分組後應用WHERE:謂詞在分組前應用
SOME vs ALL
-
SOME:滿足一個條件即為真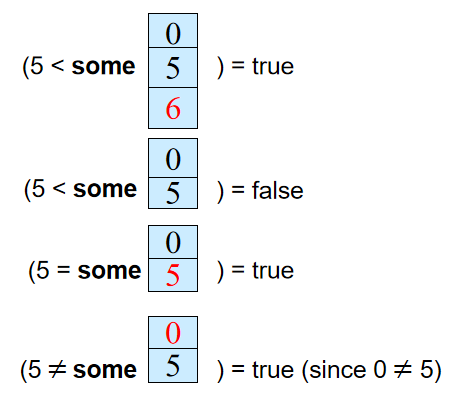
輸出所有比生物系某些老師工資高的老師的姓名。
select name from instructor where salary > SOME ( select salary from instructor where dept name = 』Biology』 ); -
ALL:滿足所有條件為真
輸出比生物學院所有教師工資都高的教師的名字。
select name from instructor where salary > ALL ( select salary from instructor where dept name = 』Biology』 );
EXISTS vs NOT EXISTS
-
EXISTS:如果在子查詢中不存在滿足條件的行,返回 false ;如果在子查詢中存在滿足條件的行,返回 trueExists 執行的流程 Exists 首先執行外層查詢,再執行記憶體查詢。流程為首先取出外層中的第一元組,再執行內層查詢,將外層表的第一元組代入,若內層查詢為真,即有結果時。返回外層表中的第一元組,接著取出第二元組,執行相同的演算法。一直到掃描完外層整表
例題:找出所有在 2018 年秋季並且在 2019 年春季開課的課程
select course_id from section as S where semester = 』Fall』 and year = 2009 and exists ( select * from section as T where semester = 』Spring』 and year= 2010 and S.course_id = T.course_id ); -
NOT EXISTS:如果在子查詢中不存在滿足條件的行,返回 true;如果在子查詢中存在滿足條件的行,返回 false。可以用於處理關係代數中的除法例題:查詢選了電腦學院開設的所有課程的學生的姓名。
SELECT student.`name` FROM student WHERE NOT EXISTS ( SELECT * FROM course WHERE course.dept_name = "Comp. Sci." AND NOT EXISTS ( SELECT * FROM takes WHERE takes.ID = student.ID AND takes.course_id = course.course_id ) );內部循環:查詢出該生沒有選擇的所有的電腦學院課程
SELECT * FROM course WHERE course.dept_name = "Comp. Sci." AND NOT EXISTS ( SELECT * FROM takes WHERE takes.ID = student.ID AND takes.course_id = course.course_id )外部循環:查詢不存在沒有選擇電腦學院所有課程的學生姓名 = 查詢選了電腦學院開設的所有課程的學生的姓名。如果該生沒有選擇的所有的電腦學院課程
NOT EXISTS則為 true,輸出。
WITH查詢
-
定義:創建一個只能查詢的臨時表
-
用法:
WITH TABLE_NAME[(FIEDL1,FIELD2...)] AS (查詢語句) -
例題:查詢平均年薪大於所有部門總平均的部門
with dept _total (dept_name, value) as ( select dept_name, sum(salary) from instructor group by dept_name ), dept_total_avg(value) as ( select avg(value) from dept_total ) select dept_name from dept_total, dept_total_avg where dept_total.value > dept_total_avg.value; -
WITH查詢可以實現遞歸查詢🌰例子 :查詢每個課程的所有前驅課程
WITH recursive rec_prereq ( course_id, prereq_id ) AS ( SELECT course_id, prereq_id FROM prereq UNION SELECT rec_prereq.course_id, prereq.prereq_id FROM rec_prereq, prereq WHERE rec_prereq.prereq_id = prereq.course_id ) SELECT * FROM rec_prereq
DML(Data Manipulation Language)
1️⃣ 增(Insertion)
# 對表中所有欄位都添加值
INSERT INTO TABLE_NAME VALUES(VALUE1,VALUE2,...);
# 對表中指定欄位添加值
INSERT INTO TABLE_NAME(FIELD1,FIELD2,...) VALUES(VALUE1,VALUE2,...);
#
INSERT INTO TABLE_NAME SELECT ... FROM
2️⃣ 刪(Deletion)
DELETE FROM TABLE_NAME [WHERE 條件]
3️⃣ 改(Updates)
UPDATE FIELD1 SET FIELD1 = ... [WHERE ...]
- 注意語句順序問題
update instructor set salary = salary * 1.03 where salary > 100000;
update instructor set salary = salary * 1.05 where salary <= 100000;
# 順序不可顛倒
可修改為使用 CASE
update instructor set salary =
case
when salary <= 100000 then salary * 1.05
else salary * 1.03
end;
DCL(Data Control Language)
- 用戶管理
1️⃣ 創建用戶
CREATE USER 用戶名[@ 主機名] [IDENTIFIED BY '密碼']
# 例子:CREATE USER 'user'@'localhost' IDENTIFIED BY '123456';
2️⃣ 查詢用戶資訊
SELECT * FROM mysql.user;
SELECT Host,User,authentication_string from mysql.user
3️⃣ 修改用戶
UPDATE mysql.user SET USER='li4' WHERE USER='wang5';
FLUSH PRIVILEGES; # 刷新資料庫
4️⃣ 刪除用戶
DROP USER 用戶名[@主機名] ;# 默認刪除host為%的用戶
# 例子:DROP USER 'tom';
- 許可權管理
1️⃣ 授予許可權
GRANT 許可權1,許可權2,…許可權n ON 資料庫名稱.表名稱 TO 用戶名@用戶地址 [IDENTIFIED BY 『密碼口令』];
# 例子:
# 給用戶『aaa』@『%』賦予所資料庫所有表的讀的許可權,但是它沒有權利給別人賦權;
grant select on *.* to 'aaa' @ '%';
# 給用戶『aaa』@『%』賦予所資料庫所有表的讀的許可權,也有權利給別人賦權;
許可權:
SELECTUPDATEDELETEINSERTALL PRIVILEGEES:代替所有許可權
2️⃣ 收回許可權
REVOKE 許可權1,許可權2,…許可權n ON 資料庫名稱.表名稱 FROM 用戶名@用戶地址;
#收回全庫全表的所有許可權
REVOKE ALL PRIVILEGES ON *.* FROM joe@'%';
#收回mysql庫下的所有表的插刪改查許可權
REVOKE SELECT,INSERT,UPDATE,DELETE ON mysql.* FROM joe@localhost;
- 須用戶重新登錄後才能生效
視圖(View)
-
定義:
- 視圖是一種 虛擬表 ,本身是 不具有數據 的,佔用很少的記憶體空間,它是 SQL 中的一個重要概念。
- 視圖建立在已有表的基礎上, 視圖賴以建立的這些表稱為基表。
- 視圖的創建和刪除隻影響視圖本身,不影響對應的基表。但是當對視圖中的數據進行增加、刪除和修改操作時,數據表中的數據會相應地發生變化,反之亦然。
- 向視圖提供數據內容的語句為 SELECT 語句, 可以將視圖理解為存儲起來的 SELECT 語句
- 視圖不會保存數據,數據真正保存在數據表中。當對視圖中的數據進行增加、刪除和修改操作時,數據表中的數據會相應地發生變化;反之亦然。
- 不建議對視圖進行修改,一般只用於查詢
-
優點:
-
操作簡單:將經常使用的查詢操作定義為視圖,可以使開發人員不需要關心視圖對應的數據表的結構、表與表之間的關聯關係,也不需要關心數據表之間的業務邏輯和查詢條件,而只需要簡單地操作視圖即可,極大簡化了開發人員對資料庫的操作。
-
減少數據冗餘:視圖跟實際數據表不一樣,它存儲的是查詢語句。所以,在使用的時候,我們要通過定義視圖的查詢語句來獲取結果集。而視圖本身不存儲數據,不佔用數據存儲的資源,減少了數據冗餘。
-
數據安全:MySQL將用戶對數據的 訪問限制 在某些數據的結果集上,而這些數據的結果集可以使用視圖來實現。用戶不必直接查詢或操作數據表。這也可以理解為視圖具有 隔離性 。視圖相當於在用戶和實際的數據表之間加了一層虛擬表。同時,MySQL可以根據許可權將用戶對數據的訪問限制在某些視圖上,用戶不需要查詢數據表,可以直接通過視圖獲取數據表中的資訊。這在一定程度上保障了數據表中數據的安全性。
-
適應靈活多變的需求 當業務系統的需求發生變化後,如果需要改動數據表的結構,則工作量相對較大,可以使用視圖來減少改動的工作量。這種方式在實際工作中使用得比較多。
-
能夠分解複雜的查詢邏輯 資料庫中如果存在複雜的查詢邏輯,則可以將問題進行分解,創建多個視圖獲取數據,再將創建的多個視圖結合起來,完成複雜的查詢邏輯。
-
-
不足:
-
難以維護:如果實際數據表的結構變更了,我們就需要及時對相關的視圖進行相應的維護.特別是嵌套的視圖(就是在視圖的基礎上創建視圖),維護會變得比較複雜, 可讀性不好 ,容易變成系統的潛在隱患。因為創建視圖的 SQL 查詢可能會對欄位重命名,也可能包含複雜的邏輯,這些都會增加維護的成本。
實際項目中,如果視圖過多,會導致資料庫維護成本的問題。
-
-
用法
# 創建視圖 CREATE VIEW 視圖名稱 AS (查詢語句) # 詳細版 CREATE [OR REPLACE] [ALGORITHM = {UNDEFINED | MERGE | TEMPTABLE}] VIEW 視圖名稱 [(欄位列表)] AS 查詢語句 [WITH [CASCADED|LOCAL] CHECK OPTION] # 增刪改查操作將視圖看作普通表即可 # 可以基於視圖創建視圖 # 修改視圖 ALTER VIEW 視圖名稱 AS 查詢語句 # 刪除視圖 DROP VIEW IF EXISTS 視圖名稱; -
不可更新視圖
- 在定義視圖的時候指定了「
ALGORITHM = TEMPTABLE」,視圖將不支援INSERT和DELETE操作; - 視圖中不包含基表中所有被定義為非空又未指定默認值的列,視圖將不支援
INSERT操作; - 在定義視圖的
SELECT語句中使用了JOIN聯合查詢 ,視圖將不支援INSERT和DELETE操作; - 在定義視圖的
SELECT語句後的欄位列表中使用了 數學表達式 或 子查詢 ,視圖將不支援INSERT,也不支援UPDATE使用了數學表達式、子查詢的欄位值; - 在定義視圖的
SELECT語句後的欄位列表中使用DISTINCT、聚合函數、GROUP BY、HAVING、UNION等,視圖將不支援INSERT、UPDATE、DELETE; - 在定義視圖的
SELECT語句中包含了子查詢,而子查詢中引用了FROM後面的表,視圖將不支援INSERT、UPDATE、DELETE; - 視圖定義基於一個不可更新視圖 ;
- 常量視圖。
- 在定義視圖的時候指定了「
存儲過程(Stored Procedure)
-
定義:
- 存儲過程是一組經過預先編譯 的 SQL 語句的封裝。預先存儲在 MySQL 伺服器上,需要執行的時候,客戶端只需要向伺服器端發出調用存儲過程的命令,伺服器端就可以把預先存儲好的這一系列 SQL 語句全部執行。
- 直接操作資料庫底層數據結構,一般用於進行更複雜的數據處理
- 沒有返回值
- 參數類型:
IN:當前參數為輸入參數,也就是表示入參;默認為IN。OUT:當前參數為輸出參數,也就是表示出參。INOUT:當前參數既可以為輸入參數,也可以為輸出參數。
- 存儲過程的功能更加強大,包括能夠執行對錶的操作(比如創建表,刪除表等)和事務操作,這些功能是存儲函數不具備的。
-
用法
# 創建存儲過程 CREATE PROCEDURE 存儲過程名(IN|OUT|INOUT 參數名 參數類型,...) [characteristics ...] BEGIN 存儲過程體 END # 刪除存儲過程 DROP PROCEDURE 存儲過程名 [IF EXISTS]; -
舉例
DELIMITER // CREATE PROCEDURE show_someone_salary2(IN empname VARCHAR(20),OUT empsalary DOUBLE) BEGIN SELECT salary INTO empsalary FROM emps WHERE ename = empname; END // DELIMITER ;DELIMITER // CREATE PROCEDURE show_mgr_name(INOUT empname VARCHAR(20)) BEGIN SELECT ename INTO empname FROM emps WHERE eid = (SELECT MID FROM emps WHERE ename=empname); END // DELIMITER ; -
調用存儲過程
# 調用in模式的參數 CALL 存儲過程名(實參列表) # 調用out模式的參數 SET @name; CALL sp1(@name); SELECT @name; # 調用inout模式的參數 SET @name=value; CALL sp1(@name); SELECT @name; # 例 1 DELIMITER // CREATE PROCEDURE CountProc(IN sid INT,OUT num INT) BEGIN SELECT COUNT(*) INTO num FROM fruits WHERE s_id = sid; END // DELIMITER ; SET @name; CALL CountProc (101, @num); SELECT @name; # 例 2 DELIMITER // CREATE PROCEDURE `add_num`(IN n INT) BEGIN DECLARE i INT; DECLARE sum INT; SET i = 1; SET sum = 0; WHILE i <= n DO SET sum = sum + i; SET i = i +1; END WHILE; SELECT sum; END // DELIMITER ; CALL add_num(50); -
優點
-
存儲過程可以一次編譯多次使用。存儲過程只在創建時進行編譯,之後的使用都不需要重新編譯,這就提升了 SQL 的執行效率。
-
可以減少開發工作量。將程式碼 封裝 成模組,實際上是編程的核心思想之一,這樣可以把複雜的問題拆解成不同的模組,然後模組之間可以 重複使用 ,在減少開發工作量的同時,還能保證程式碼的結構清晰。
-
存儲過程的安全性強。我們在設定存儲過程的時候可以設置對用戶的使用許可權 ,這樣就和視圖一樣具有較強的安全性。
-
可以減少網路傳輸量。因為程式碼封裝到存儲過程中,每次使用只需要調用存儲過程即可,這樣就減少了網路傳輸量。
-
良好的封裝性。在進行相對複雜的資料庫操作時,原本需要使用一條一條的 SQL 語句,可能要連接多次資料庫才能完成的操作,現在變成了一次存儲過程,只需要 連接一次即可 。
-
-
缺點:
-
可移植性差。存儲過程不能跨資料庫移植,比如在 MySQL、Oracle 和 SQL Server 里編寫的存儲過程,在換成其他資料庫時都需要重新編寫。
-
調試困難。只有少數 DBMS 支援存儲過程的調試。對於複雜的存儲過程來說,開發和維護都不容易。雖然也有一些第三方工具可以對存儲過程進行調試,但要收費。
-
存儲過程的版本管理很困難。比如數據表索引發生變化了,可能會導致存儲過程失效。我們在開發軟體的時候往往需要進行版本管理,但是存儲過程本身沒有版本控制,版本迭代更新的時候很麻煩。
-
它不適合高並發的場景。高並發的場景需要減少資料庫的壓力,有時資料庫會採用分庫分表的方式,而且對可擴展性要求很高,在這種情況下,存儲過程會變得難以維護, 增加資料庫的壓力 ,顯然就不適用了。
-
阿里開發規範
【強制】禁止使用存儲過程,存儲過程難以調試和擴展,更沒有移植性。
函數(Function)
-
定義:
MySQL支援自定義函數,定義好之後,調用方式與調用MySQL預定義的系統函數一樣。- 有返回值
- 用戶自己定義的存儲函數與MySQL內部函數是一個性質的。區別在於,存儲函數是 用戶自己定義 的,而內部函數是
MySQL的開發者定義的。 - 參數類型:總是默認為
IN參數。 RETURNS子句只能對FUNCTION做指定,對函數而言這是強制的。它用來指定函數的返回類型,而且函數體必須包含一個RETURN value語句。- 存儲函數可以放在查詢語句中使用,存儲過程不行
-
用法
# 創建函數 CREATE FUNCTION 函數名(參數名 參數類型,...) RETURNS 返回值類型 [characteristics ...] BEGIN 函數體 #函數體中肯定有 RETURN 語句 END # 刪除函數 DROP FUNCTION 函數名 [IF EXISTS] -
調用函數
SELECT 函數名(實參列表) -
舉例
DELIMITER // CREATE FUNCTION count_by_id(dept_id INT) RETURNS INT LANGUAGE SQL NOT DETERMINISTIC READS SQL DATA SQL SECURITY DEFINER COMMENT '查詢部門平均工資' BEGIN RETURN (SELECT COUNT(*) FROM employees WHERE department_id = dept_id); END // DELIMITER ; SET @dept_id = 50; SELECT count_by_id(@dept_id);
實體聯繫模型(Entity-Relationship Model)
建模(Modeling)
ER 模型中的三個基本概念
-
實體集(Entity Sets)

-
實體:是一個存在的物體,且區別於其他物體。實體可以表示為一組屬性的集合
-
實體集:是具有相同類型,共享相同屬性的實體的集合。
-
一個或一些屬性形成主鍵(pirmary key)可唯一區分實體集中的每一個實體
-
強實體集(Strong Entity Sets):有主碼的實體集,通過主碼區分每一個實體
-
弱實體集(Weak Entity Sets):沒有足夠的屬性以形成主碼的實體集
-
每個弱實體集必須與一個標識實體集(強實體集)建立聯繫。
-
與弱實體集建立聯繫的聯繫集叫做標識性聯繫(Identifying Relationship)。
-
雖然弱實體集沒有主碼,但是我們仍需要區分依賴於特定強實體集的弱實體集中的實體的方法。弱實體集的分辨符(discriminator)是使得我們進行這種區分的屬性集合。
-
弱實體集的主碼由標識實體集的主碼加上該弱實體集的分辨符構成。
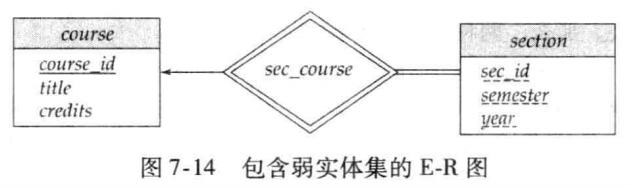
🌰 圖 7-14 中弱實體集
section的主碼由course_id,sec_id,semester,year組成。其中course_id是course的主碼,sec_id,semester,year是section的分辨符,用於區分每個course的不同section。
-
-
-
聯繫集(Relationship Sets)
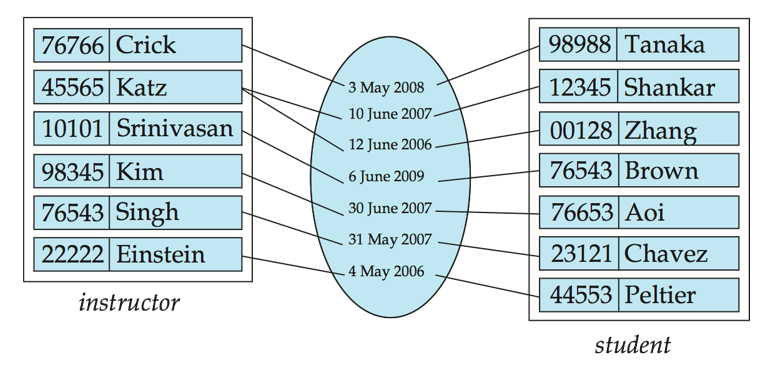
- $ \left{ \left( e_1,e_2,…e_n \right) |e_1\in E_1,e_2\in E_2,…,e_n\in E_n \right} $
- 連接兩個或多個實體
- 聯繫集也可以有屬性
- 聯繫集的度(Degree of a Relationship Set):即連接實體集的個數,多數情況聯繫集是二元聯繫(binary relationship),很少有多元聯繫。
-
屬性(Attributes)
-
單值和多值屬性(Single-valued and multivalued Attributes):例如,人有多個電話號碼,是多值
-
簡單和複合屬性(Simple and composite Attributes):例如,英文名可拆分為 first name ,last name ,是複合屬性
-
派生屬性(Derived Attributes):可以從其他別的屬性或實體派生出來。例如:年齡(根據出生日期和當前日期計算得出)
-
冗餘屬性(Redundant Attributes)
-
域(Domain):每個屬性的取值範圍
-
映射基數約束(Mapping Cardinality Constraints)
-
定義:表示一個實體通過一個聯繫集能夠關聯的實體的個數
-
對於二元關係集,映射基數包含如下四種類型
-
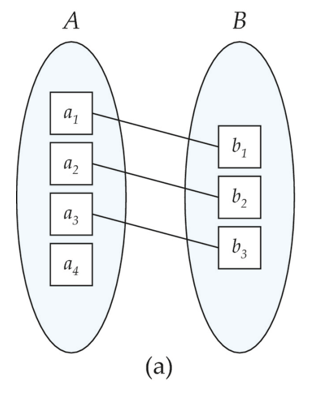
一對一(One to one)
-
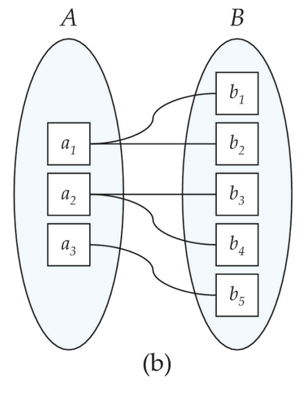
一對多(One to many)
-
多對一(Many to one)
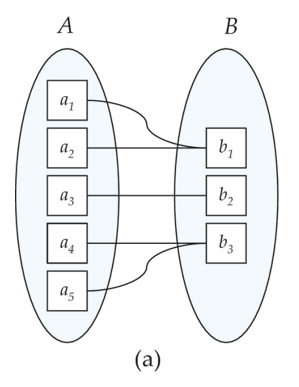
-
多對多(Many to many)
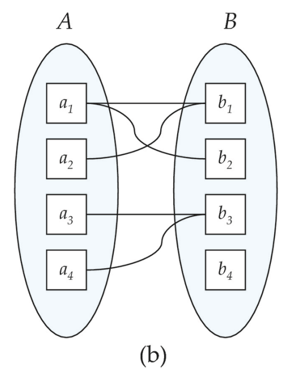
-
實體-聯繫圖(E-R Diagrams)
1️⃣ 實體:矩形表示實體,屬性寫矩形內部,下劃線表示主碼

2️⃣ 聯繫:菱形表示聯繫(聯繫可以有屬性)
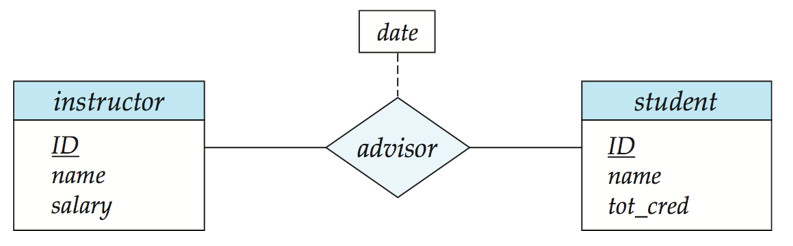
3️⃣ 連線:只能連接實體和屬性、實體和聯繫,不能連接實體和實體或聯繫和聯繫
4️⃣ 屬性:
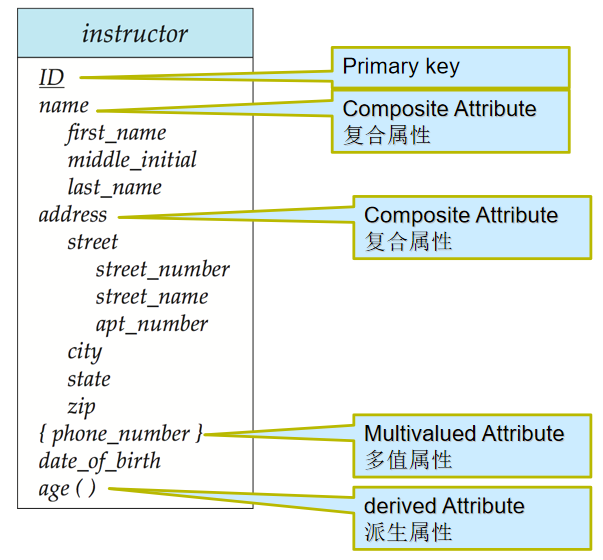
5️⃣ 角色(Roles):實體在聯繫中扮演的功能叫做實體的角色。當相同實體集在聯繫中扮演不同的角色的時候(自連接),需顯示標記角色資訊

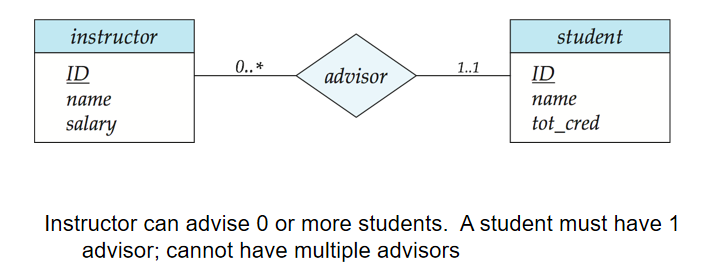
6️⃣ 基數約束(Cardinality Constraints):
- 聯繫集指向實體集
- 有向連線➡️表示一個(One)
- 無向連線➖表示多個(Many)
一個 instructor 通過 advisor 與若干(包括 0)student 聯繫(0..*)
一個 student 通過 advisor 與最多一個 instructor 聯繫(1..1)

-
表達更複雜的映射基數約束
l..h:l表示基數最小值,h表示基數最大值
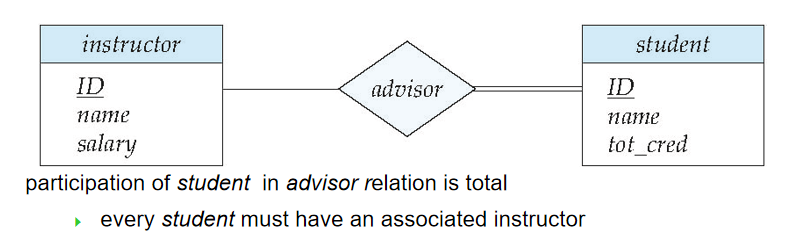
7️⃣ 全參與和部分參與(Total and Partial Participation)
- 全參與:每個實體至少參與了聯繫集中的某一個聯繫(雙線)
- 部分參與:某些實體可能未參與聯繫集中的任何一個聯繫(單線)
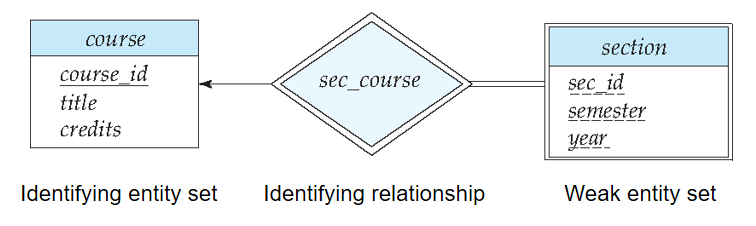
8️⃣ 弱實體集(Weak Entity Sets)
- 弱實體集表示為雙層矩形
- 弱實體集的分辨符用虛下劃線標出
- 弱實體集和標誌性強實體集間的聯繫集用雙層菱形表示。
- 弱實體集與標識實體集之間必然是多對一關係,且弱實體集的實體全部參與
轉化為關係模式(Reduction to Relation Schemas)
- 實體集和聯繫集都可以轉化為關係模式,用以存儲資料庫中的內容
- 若資料庫符合 E-R 圖,則可以表示成模式的集合
- 在 E-R 圖中,每個實體集和聯繫集均對應一個唯一的模式
- 在每個模式中,均有多個列,且模式內列名不重複。
1️⃣ 強實體集使用相同屬性轉化成關係模式
🌰 例如
強實體集:
關係模式: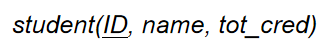
2️⃣ 弱實體集包含標誌性強實體集中的主碼。
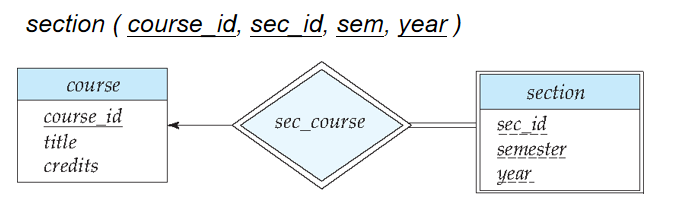
3️⃣ 對於聯繫集:
- 多對多的聯繫集也應表示成關係模式,其屬性包含參與該聯繫的實體集的主碼的並集和它自身的描述屬性。
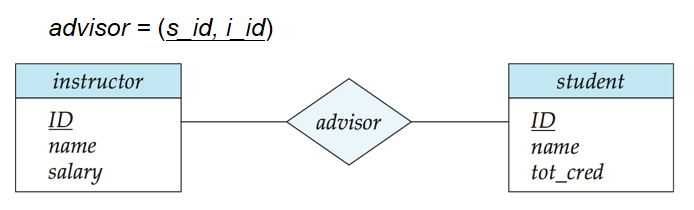
同一實體集內部多對多:

- 多對一或一對多的聯繫集不轉化為關係模式,而是將多(Many)的一端的實體集中加入一(One)那一端的實體集的主碼。
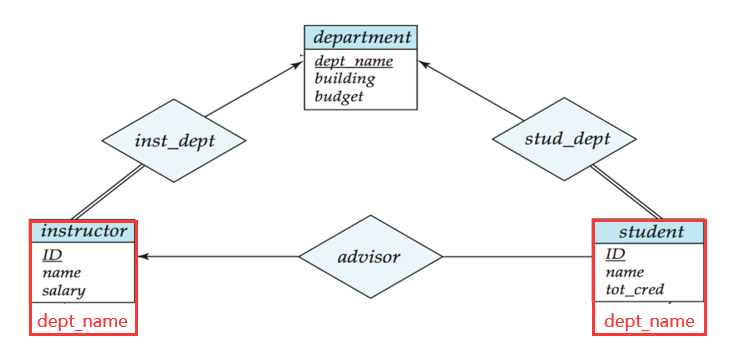
自引用(同一實體集內部不同實體之間多對一):
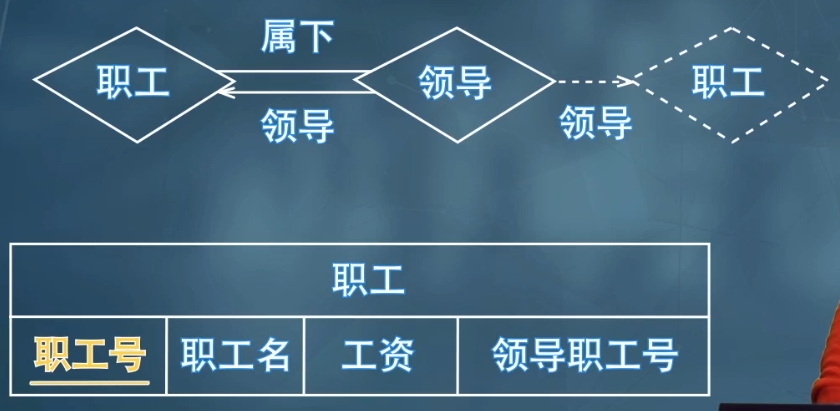
- 一對一的關係集可將任意一端看作多的那一端。如果多的那一端的實體集是部分參與的,轉化成關係模式之後,有些元組的屬性中會出現 NULL。
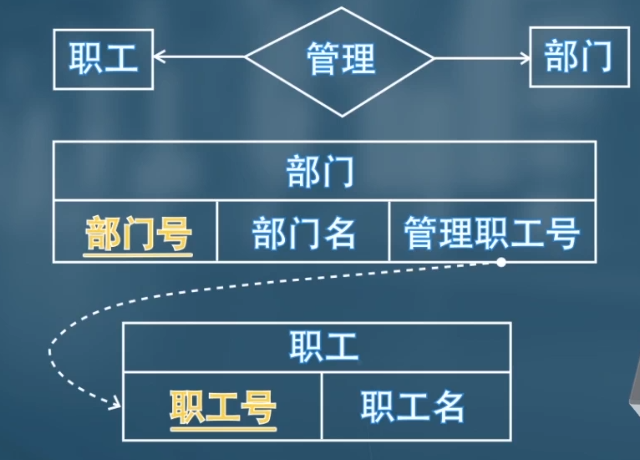
- 一般情況下,連接弱實體集與其所依賴的強實體集的聯繫集的模式是冗餘的,而且在基於 E-R 圖的關係資料庫設計中不必給出。實體集當成多對一處理即可。
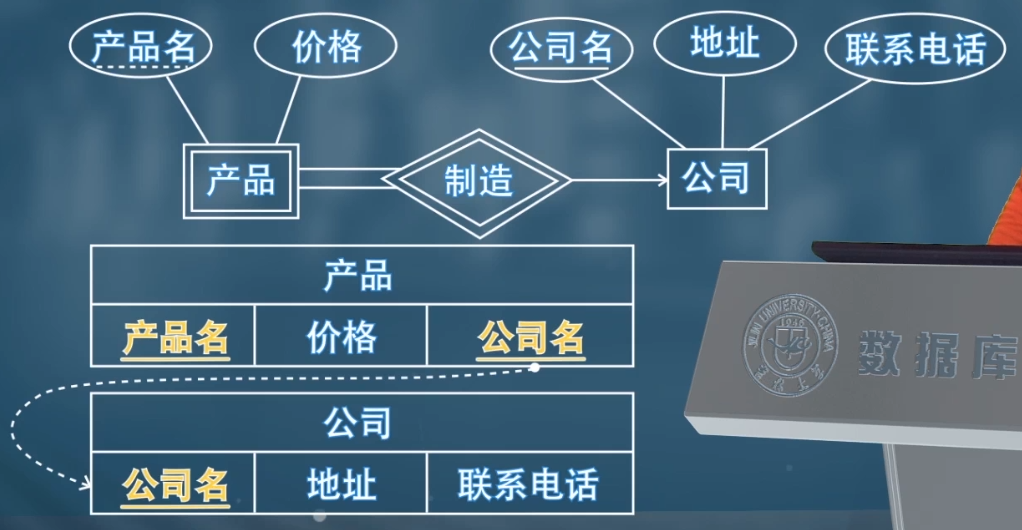
4️⃣ 對於屬性:
- 複合屬性忽視所有父級屬性,將子屬性創建單獨的屬性
- 忽視多值屬性,將多值屬性表示成一個單獨的模式 EM(原實體集 E,多值屬性 M)。多值屬性的每一個取值都會映射成為這個新的模式內的一條元組
- 忽視派生屬性



5️⃣ 對於特化

-
低層實體轉化成模式的時候,只包含高層模式的主碼和自己獨有屬性

缺點:獲取低層實體繼承的屬性時需要訪問高層實體。
-
每個實體集對應的模式中記錄所有的屬性,包括局部和繼承的屬性。

缺點:數據冗餘
6️⃣ 對於聚集:
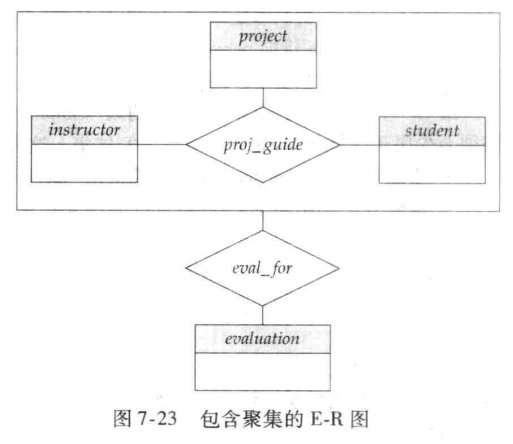
表示聚集和實體集之間聯繫的聯繫集(eval_for)需要包含:
-
聚集聯繫的主碼(i_ID,s_ID,project_ID)
-
關聯實體集的主碼(evaluation_ID)
-
聯繫集的描述屬性


實體-聯繫設計問題(Design Issues)
1. 用實體集還是用屬性
沒有一個固定的說法,需要依據企業實際情況進行設計。
定義為實體集可以添加更多的拓展資訊,但會造成查詢時損失效率。
定義為屬性可以提高查詢速度,方便查詢,但會造成資訊缺失,拓展性差。
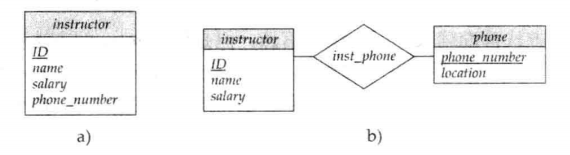
🔔 有兩個常犯的錯誤:
1️⃣ 用一個實體集的主碼作為另一個實體集的屬性,而不是用聯繫。例如,即時每名教師只指導一名學生,將 student 的 ID 作為 instructor 的屬性也是不正確的。用 advisor 聯繫代表學生和教師之間的關聯才是正確的方法,因為這樣可以明確地表示出兩者之間的關係而不是將這種關係隱含在屬性中。
2️⃣ 將相關實體集的主碼屬性作為聯繫集的屬性。例如,ID ( student 的主碼屬性) 和 ID( instructor 的主碼)不應該在 advisor 聯繫中作為屬性出現。這樣做是不對的,因為在聯繫集中已經隱含了這些主碼屬性。
2. 用實體集還是用聯繫集
原則:當描述發生在實體間的行為時採用聯繫集。
有的時候用實體集實體集還是聯繫集都可以,這個時候推薦根據原則進行重新考慮。
有的時候則只能使用實體集或聯繫集。
🌰 例如:購物系統,用戶只能通過代理購買商品,定義三個實體集 customer ,production,Agent
下面考慮用實體集還是聯繫集將三個實體集聯繫起來,如果使用聯繫集 order
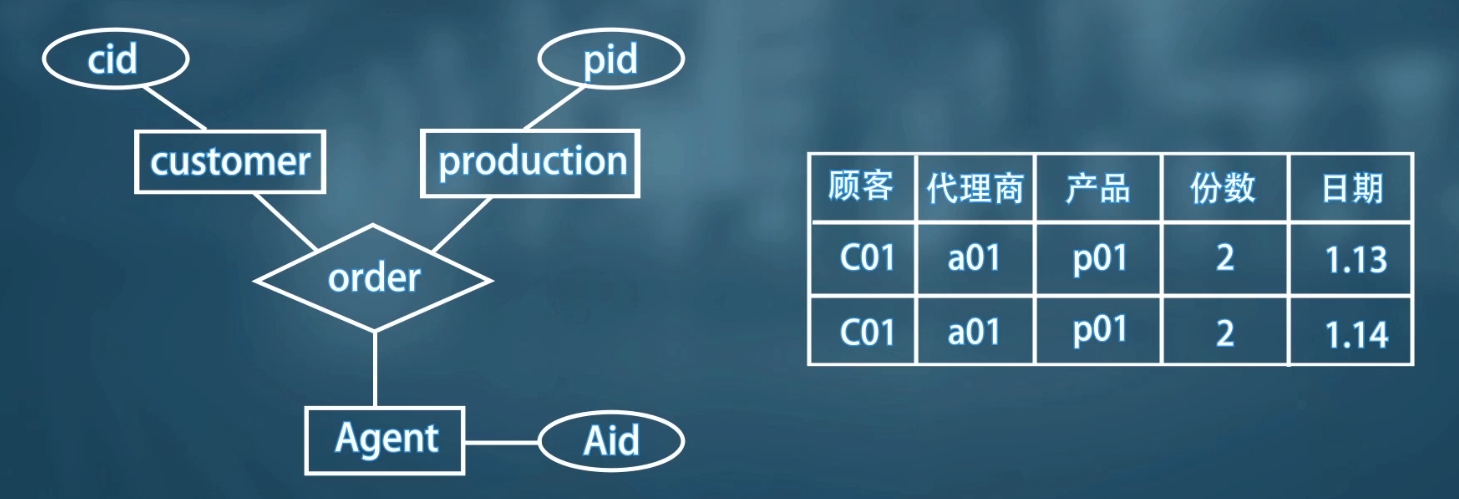
根據 E-R 圖的定義,多對多時,聯繫集轉化成關係時主鍵由所有與其聯繫的實體集的主鍵組成(顧客、代理商、產品),聯繫集可以有自己的屬性(份數,日期)。這是發現,無法通過 order 的主鍵唯一區分一條記錄。
應該使用實體集。

3. 二元還是 n 元聯繫集
資料庫通常是二元聯繫,但有的聯繫用 n 元聯繫集表示更清晰。
一個 n(n > 2) 元聯繫總可以用一組二元聯繫代替。
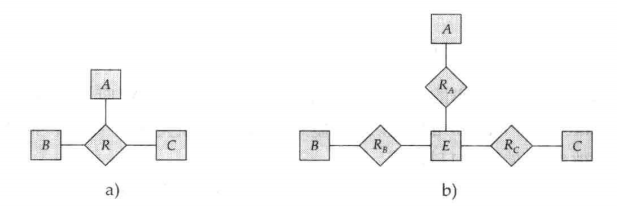
a):R(a,b,c)
b):E(e,a,b,c),RA(e,a),RB(e,b),RC(e,c)
一些限制:
- 對於為表示聯繫集而創建的實體集,我們可能不得不為其創建一個標識屬性。該標識屬性和額外所需的那些聯繫集增加了設計的複雜程度以及對總的存儲空間的需求
- n 元聯繫集可以更清晰地表示幾個實體集參與單個聯繫集。
- 有可能無法將三元聯繫上的約束轉變為二元聯繫上的約束。例如,考慮一個約束,表明 R 是從A、B 到 C 多對一的;也就是,來自 A 和 B 的每一對實體最多與一個 C 實體關聯。這種約束就不能用聯繫集 RA、RB 和 RC 上的基數約束來表示。
4. 聯繫集的屬性布局
考慮聯繫集中放置什麼屬性。
一對一聯繫集的屬性可以放到任意一個與其聯繫的實體集中。
一對多或多對一聯繫集的屬性可以放到「多方」的實體集中.
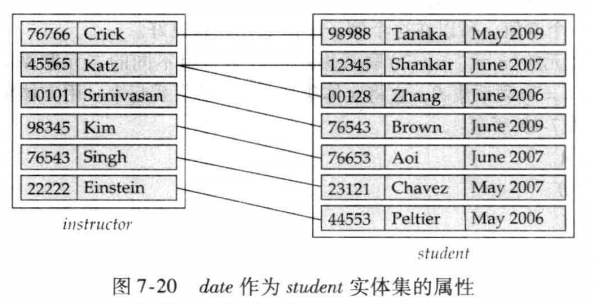
🌰 例如:student 和 instructor 通過 advisor 建立多對一聯繫,聯繫集 advisor 中有 date 屬性記錄學生選擇導師的時間,該屬性可以放在 student 實體集中,等價於放在聯繫集中。
拓展的 E-R 特性(Advanced Topics)
1. 特化(Specialization)
在實體集內部根據某些條件進行分組的過程稱為特化。
🌰 例如:person 可以根據職位分成 student 和 employee 兩個組,而 employee 又可以分為 instructor 和 secretary 兩個組。
-
自頂向下的設計過程,一個實體集可以分為多個子集。類比面向對象設計中的繼承。
-
這些子集變成更低層的實體集,會包含一些高層實體集沒有的屬性,參與一些高層實體集沒有的聯繫。
-
由標記為
ISA的三角形組件描述。 -
屬性的繼承(Attribute inheritance):低層的實體集自動繼承了其對應的高層實體集的所有屬性和聯繫。
-
重疊特化(Overlapping Specialization):一個實體集可能屬於多個特化實體集。例如,一個特定的僱員可以既是一個臨時的僱員,又是一個秘書。
-
不相交特化(Disjoint Specialization):一個實體集必須屬於至多一個特化實體集。

2. 概化(Generalization)
將一些具有相同屬性的實體集合併成一個更高級別的實體集的過程稱為概化。
-
自底向上的設計過程。
-
特化和概化是兩個互逆的操作。在ER圖中表示方法相同。
-
特化和概化可以互換。
-
概化的進行基於這樣的認識:一定數量的實體集共享一些共同的特徵(即用相同的屬性描述它們,且它們都參與到相同的聯繫集中)。概化是在這些實體集的共性的基礎上將它們綜合成一個高層實體集。概化用於強調低層實體集間的相似性並隱藏它們的差異;由於共享屬性的不重複出現,它還使得表達簡潔。
3. 聚集(Aggregation)
聚集是一種抽象,通過這種抽象,聯繫被視為高層實體。可以表達聯繫間的聯繫。
🌰 例如:

eval_for 中的每個 instructor,student,project 組合肯定在 proj_guide 中,造成數據冗餘。

一個學生在一個特定的項目中受一名老師指導。
學生、老師和項目的組合關聯一個評估實體。
聚集之後的高層實體集 proj_guide 可以當作其他實體集處理。
關係資料庫設計(Relational Database Design)
好的關係設計特點(Features of Good Relational Design)
有損分解(A Lossy Decomposition):原表經過分解之後進行自然連接,如果形成的表與原表相同則為無損分解;否則為有損分解

原子域和第一範式(Atomic Domains and First Normal Form)
一個域是原子的(atomic ),如果該域的元素被認為是不可分的單元。
我們稱一個關係模式 R 屬於第一範式(First Normal Form,1NF),如果 R 的所有屬性的域都是原子的。
使用函數依賴進行分解(Decomposition Using Functional Dependencies)
函數依賴(Functional Dependencies)
-
定義:
-
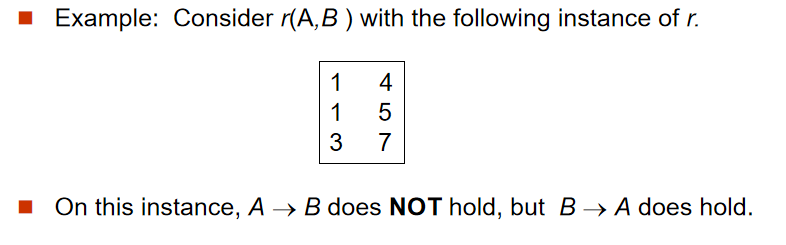
對於聯繫 R ,如果有屬性集合 $ \alpha \subseteq R$ ,$ \beta \subseteq R $ ,給定 r(R) 的一個實例,我們說這個實例滿足函數依賴 $ \alpha \rightarrow \beta $ 的條件是:對實例中所有元組對 t1 和 t2,若 t1[ $ \alpha $ ] = t2[ $ \alpha $ ],則 t1[ $ \beta $ ] = t2[ $ \beta $ ]
-
如果在 r(R) 的每個合法實例中都滿足函數依賴 $ \alpha \rightarrow \beta $ ,則我們說函數依賴在模式 r(R) 上成立(hold)。
-
-
是合法關係上的約束
-
一個屬性集上的取值應該可以唯一確定另外一組屬性上的取值
-
函數依賴是碼約束的泛化
-
函數依賴能使我們表達超碼錶達不了的約束
-
碼的函數依賴
- 超碼(super key):$ K \rightarrow R $
- 候選碼(candidate key): $ K \rightarrow R $ and for no $ \alpha \subset K $ ,$ \alpha \rightarrow R $ (沒有元組子集能蘊含 R)
-
平凡函數依賴(trivial):在所有關係中都滿足
-
$ \alpha \rightarrow \alpha $
-
$ \alpha \rightarrow \beta $, if $ \beta \subseteq \alpha $
-
-
函數依賴的閉包(closure)
- 給定一個函數依賴集 $ F $,有可能會推斷出某些其他的函數依賴。
- 由 $ F $ 推斷出來的所有依賴構成 $ F $ 的閉包,記作 $ F^+ $
- $ F^+ $ 是 $ F $ 的超集
Boyce Codd 範式
-
定義:具有函數依賴集 $ F $ 的關係模式 $ R $ 屬於 $ BCNF $ 的條件是,對 $ F^+ $ 中所有形如 $ \alpha \rightarrow \beta $ 的函數依賴(其中 $ \alpha \subseteq R$ ,$ \beta \subseteq R $ ),下面至少有一項成立:
- $ \alpha \rightarrow \beta $ 是平凡的函數依賴,(即, $ \beta \subseteq \alpha $)
- $ \alpha $ 是模式 $ R $ 的一個超碼
-
BC範式是我們能達到的比較滿意的範式之一。它能消除所有利用函數依賴發現的冗餘。
-
一個資料庫設計屬於$ BCNF$ 的條件是,構成該設計的關係模式集中的每個模式都屬於 \(BCNF\)。


-
將模式分解成BCNF(Decomposing a Schema into BCNF)
- 設 \(R\) 為不屬於 \(BCNF\) 的一個模式。則存在至少一個非平凡的函數依賴 $ \alpha \rightarrow \beta $ ,其中 $ \alpha $ 不是 \(R\) 的超碼。我們在設計中用一下兩個模式取代 \(R\)。形成兩個模式。
- $ \left( \alpha \cup \beta \right) $
- $ \left( R-\left( \beta -\alpha \right) \right) $
- 當我們分解不屬於 \(BCNF\) 的模式時,產生的模式中可能有一個或多個不屬於 \(BCNF\)。在這種情況中,需要進一步分解,其最終結果是一個 \(BCNF\) 模式集合。
- 設 \(R\) 為不屬於 \(BCNF\) 的一個模式。則存在至少一個非平凡的函數依賴 $ \alpha \rightarrow \beta $ ,其中 $ \alpha $ 不是 \(R\) 的超碼。我們在設計中用一下兩個模式取代 \(R\)。形成兩個模式。
-
BCNF 和保持依賴
- 如果分解後,每個依賴都得以保存,則稱該分解為依賴保持分解。
- 由於常常希望保持依賴,因此我們考慮另外一種比 $BCNF $ 弱的範式它允許我們保持依賴。該範式稱為第三範式。
第三範式(third normal form)
-
定義:具有函數依賴集 \(F\) 的關係模式 \(R\) 屬於第三範式(third normal form)的條件是:對於 \(F^+\) 中所有形如 \(\alpha \rightarrow \beta\) 的函數依賴(其中 $ \alpha \subseteq R$ ,$ \beta \subseteq R $ ),以下至少一項成立:
- \(\alpha \rightarrow \beta\) 是一個平凡的函數依賴
- \(\alpha\) 是 \(R\) 的一個超碼
- \(\beta – \alpha\) 中的每個屬性 \(A\) 都包含於 \(R\) 的一個候選碼中
-
注意上面的第三個條件並沒有說單個候選碼必須包含 \(\beta – \alpha\) 中的所有屬;\(\beta – \alpha\)中 的每個屬性 A 可能包含於不同的候選碼中。
-
注意任何滿足 \(BCNF\) 的模式也滿足 \(3NF\),\(BCNF\) 是比 \(3NF\) 更嚴格的範式。
-
\(3NF\) 的定義允許某些 \(BCNF\) 中不允許的函數依賴。
函數依賴理論(Functional Dependency Theory)
阿姆斯特朗公理(Armstrong』s Axioms)
- 自反律(reflexivity rule):若 \(\alpha\) 為一屬性集且 $ \beta \subseteq \alpha $ ,則 \(\alpha \rightarrow \beta\) 成立。
- 增補律(augmentation rule):若 \(\alpha \rightarrow \beta\) 成立且 \(\gamma\) 為一屬性集,則 \(\gamma \alpha \rightarrow \gamma \beta\) 成立。
- 傳遞律(transitivity rule):若 \(\alpha \rightarrow \beta\) 和 \(\beta \rightarrow \gamma\) 成立,則 \(\alpha \rightarrow \gamma\) 成立。
根據以上三個公理可以推導出一些規則:
-
合併律(union rule):若 \(\alpha \rightarrow \beta\) 和 \(\alpha \rightarrow \gamma\) 成立,則 \(\alpha \rightarrow \beta \gamma\) 成立。
🍗 證明:
\(\alpha \rightarrow \beta\) (題目已知)1️⃣
$ \alpha \gamma \rightarrow \beta \gamma$ (增補律)2️⃣
\(\alpha \rightarrow \gamma\) (題目已知)3️⃣
\(\alpha \alpha \rightarrow \alpha \gamma\) (增補律)4️⃣
即 \(\alpha \rightarrow \alpha \gamma\) 5️⃣
由 2️⃣ 和 5️⃣ 得 \(\alpha \rightarrow \beta \gamma\) (傳遞律)
-
分解律(decomposition):若 \(\alpha \rightarrow \beta \gamma\) 成立,則 \(\alpha \rightarrow \beta\) 和 \(\alpha \rightarrow \gamma\) 成立。
🍖 證明:
\(\alpha \rightarrow \beta \gamma\) (題目已知)1️⃣
由 \(\beta \subseteq \beta \gamma\) 得 \(\beta \gamma \rightarrow \beta\) (自反律)2️⃣
由 \(\gamma \subseteq \beta \gamma\) 得 \(\beta \gamma \rightarrow \gamma\) (自反律)3️⃣
由 1️⃣ 和 2️⃣ 得 \(\alpha \rightarrow \beta\) (傳遞律)
由 1️⃣ 和 3️⃣ 得 \(\alpha \rightarrow \gamma\) (傳遞律)
-
偽傳遞律(pseudotransitivity rule):若 \(\alpha \rightarrow \beta\) 和 \(\gamma \beta \rightarrow \delta\) 成立,則 \(\alpha \gamma \rightarrow \delta\) 成立。
🍔 證明:
\(\alpha \rightarrow \beta\) (題目已知)1️⃣
\(\alpha \gamma \rightarrow \beta \gamma\) (增補律)2️⃣
即 \(\alpha \gamma \rightarrow \gamma \beta\) 3️⃣
\(\gamma \beta \rightarrow \delta\) (題目已知)4️⃣
由 3️⃣ 和 4️⃣ 得 \(\alpha \gamma \rightarrow \delta\) (傳遞律)
屬性集的閉包(Closure of Attribute Sets)
如果 \(\alpha \rightarrow \beta\) ,我們稱屬性 B 被 \(\alpha\) 函數確定(functionally determine)。要判斷集合 \(\alpha\) 是否為超碼,我們必須設計一個演算法,用於計算被 \(\alpha\) 函數確定的屬性集。一種方法是計算 \(F^+\),找出所有左半部為 \(\alpha\) 的函數依賴,併合並這些函數依賴的右半部。但是這麼做開銷大,因為 \(F^+\) 可能很大。
令 \(\alpha\) 為一個屬性集。我們將函數依賴集 \(F\) 下被 \(\alpha\) 函數確定的所有屬性的集合稱為 \(F\) 下 \(\alpha\) 的閉包,記為 \(\alpha ^+\) 。
設計一個演算法:

🐍 實例模擬:
R = (A, B, C, G, H, I)
F = {A \(\rightarrow\) B A \(\rightarrow\) C CG \(\rightarrow\) H CG \(\rightarrow\) I B \(\rightarrow\) H}
$\left( AG \right) ^+ $
- result = AG
- result = ABCG (A \(\rightarrow\) C and A \(\rightarrow\) B)
- result = ABCGH (CG \(\rightarrow\) H and CG \(\subseteq\) AGBC)
- result = ABCGHI (CG \(\rightarrow\) I and CG \(\subseteq\) AGBCH)
故 \(AG\) 的閉包 \(AG^+\) 為 ABCGHI
🌜 \(AG\) 是不是超碼:看 \(AG^+\) 能否唯一區分 \(R\) 的元組,即判斷 \(R\) 是否包含於 \(AG^+\) 。由於 \(R \subseteq AG ^+\) ,得 \(AG\) 是超碼
🌛 \(AG\) 是不是候選碼:對 \(AG\) 的所有真子集求閉包,如果存在一個真子集的閉包可以唯一區分 \(R\) 的元組,則不是候選碼。
🔔 屬性閉包的多種用途:
1️⃣ 為了判斷 \(\alpha\) 是否為超碼,我們計算 \(\alpha^+\) ,檢查 \(\alpha^+\) 是否包含 \(R\) 中的所有屬性
2️⃣ 通過檢查是否 \(\beta \subseteq \alpha^+\) ,我們可以檢查函數依賴 \(\alpha \rightarrow \beta\) 是否成立(或換句話說,是否屬於 \(F^+\))。也就是說,我們用屬性閉包計算 \(\alpha^+\),看它是否包含 \(\beta\)。
3️⃣ 該演算法給了我們另一種計算 \(F^+\) 的方法:對任意的 \(\gamma \subseteq R\),我們找出閉包 \(\gamma^+\);對任意的 \(S \subseteq \gamma^+\),我們輸出一個函數依賴 \(S \subseteq \gamma^+\)
🌌 候選鍵的計算:
-
定義:
- 左部屬性,只出現在 F 左邊的屬性
- 右部屬性,只出現在 F 右邊的屬性
- 雙部屬性,出現在 F 兩邊的屬性
- 外部屬性,不出現在 F 中的屬性
-
定理:
- 左部屬性一定出現在任何候選碼中
- 右部屬性一定不出現在任何候選碼中
- 外部屬性一定出現在任何候選碼中
- 雙部屬性可能出現在候選碼中
-
求所有候選鍵可以通過左部屬性與每一個雙部屬性組合然後求閉包。也要單獨考慮雙部屬性是不是候選碼。


正則覆蓋(Canonical Cover)
-
無關屬性(Extraneous Attribute):
- 定義:如果去除函數依賴中的一個屬性不改變該函數依賴集的閉包,則稱該屬性是無關的
- 形式化定義:考慮函數依賴集 \(F\) 及 \(F\) 中的函數依賴 \(\alpha \rightarrow \beta\)
- 如果 \(A \in \alpha\) 並且 \(F\) 邏輯蘊含 $ \left( F-\left{ \alpha -\beta \right} \right) \cup \left{ \left( \alpha -A \right) \rightarrow \beta \right} $ ,則屬性 \(A\) 在 \(\alpha\) 中是無關的。
- 如果 \(A \in \beta\) 並且函數依賴集 $ \left( F-\left{ \alpha -\beta \right} \right) \cup \left{ \alpha \rightarrow \left( \beta -A \right) \right} $ 邏輯蘊含 \(F\) ,則屬性 \(A\) 在 \(\beta\) 中是無關的。
- 無關屬性只可能出現在依賴一段超過一個屬性的情況下。🌰 例如,假定我們在 \(F\) 中有函數依賴 AB→C 和 A→C,那麼 B 在AB→C 中是無關的。再比如,假定我們在F中有函數依賴 AB→CD 和 A→C,那麼 C 在 AB→CD 的右半部中是無關的。
-
正則覆蓋(Canonical Cover)\(F_c\) 是與 \(F\) 等價的最小的函數依賴集合。
- \(F_c\) 是一個依賴集,使得 \(F\) 中邏輯蘊含 \(F_c\) 中的所有依賴,並且 \(F_c\) 邏輯蘊含 \(F\) 中的所有依賴。
- \(F_c\) 中任何函數依賴都不含無關屬性。
- \(F_c\) 中函數依賴的左半部都是唯一的。即,\(F_c\) 中不存在兩個依賴 \(\alpha_1 \rightarrow \beta_1\) 和 \(\alpha_2 \rightarrow \beta_2\) ,滿足 \(\alpha_1 = \alpha_2\) 。
-
計算無關屬性(Computing a Extraneous Attribute)
- 左邊屬性無關:\(A \in \alpha\) ,\(A\) 疑似為無關屬性。在 \(F\) 上計算 $ \left( \left{ \alpha \right} -A \right) ^+$ ,如果該閉包中包含 \(\beta\) 則說明 \(A\) 是 \(\alpha\) 中的無關屬性。
- 右邊屬性無關:$ A \in \beta$ ,\(A\) 疑似為無關屬性。在 \(F’=\) $ \left( F-\left{ \alpha -\beta \right} \right) \cup \left{ \alpha \rightarrow \left( \beta -A \right) \right} $ 上計算 $ \alpha^+$ ,如果該閉包中包含 \(\beta\) 則 \(A\) 是 \(\beta\) 中的無關屬性。
-
計算正則覆蓋(Computing a Canonical Cover)

- 合併相同的左部屬性。
- 計算無關屬性(先左再右)並刪除。
- 循環直到 \(F_c\) 不變。
- 由於順序不同,計算出的正則覆蓋可能不同。
🐍 實例模擬:
R = (A, B, C)
F = {A \(\rightarrow\) BC,B \(\rightarrow\) C,A \(\rightarrow\) B,AB \(\rightarrow\) C}
1️⃣ 合併 A \(\rightarrow\) BC,A \(\rightarrow\) B 得到 A \(\rightarrow\) BC,F = {A \(\rightarrow\) BC,B \(\rightarrow\) C,AB \(\rightarrow\) C}
2️⃣ 檢查 A 是不是 AB \(\rightarrow\) C 中的無關屬性。\(\left( \alpha – A \right) = B\) ,\(\left(\alpha – A \right)^+=BC\) 包含 \(\beta = C\) ,則 A 是無關屬性,去掉 A 得 B \(\rightarrow\) C
3️⃣ F = {A \(\rightarrow\) BC,B \(\rightarrow\) C}
4️⃣ 考慮 C 是不是 A \(\rightarrow\) BC 中的無關屬性。$ F’ $ = {B \(\rightarrow\) C,A \(\rightarrow\) B},\(\alpha=A\) ,\(\alpha^+\)=ABC 包含 \(\beta=BC\) ,則 C 是無關屬性,去掉 C 得 A \(\rightarrow\) B
5️⃣ F = {A \(\rightarrow\) B,B \(\rightarrow\) C}
無損連接(lossless decomposition)
-
定義:令 \(r \left( R \right)\) 為一個關係模式,F 為 \(r \left( R \right)\) 上的函數依賴集。令 \(R_1\) 和 \(R_2\) 為 R 的分解。如果用兩個關係模式 $r_1 \left( R_1 \right) $ 和 $r_2 \left( R_2 \right) $替代 \(r \left( R \right)\) 時沒有資訊損失,則我們稱該分解是無損分解(lossless decomposition)。更
-
判斷無損連接:$ r=\prod\nolimits_{R_1}^{}{\left( r \right) \Join}\prod\nolimits_{R_2}^{}{\left( r \right)} $
我們可以用函數依賴來說明什麼情況下分解是無損的。令\(R_1\),和 \(R_2\) ,是 \(R\) 的無損分解,如果以下函數依賴中至少有一個屬於 \(F^+\) :
- \(R_1 \cap R_2 \rightarrow R_1\)
- \(R_1 \cap R_2 \rightarrow R_2\)
換句話說,如果 \(R_1 \cap R_2\) 是 \(R_1\) 或 \(R_2\) 的超碼,\(R\) 上的分解就是無損分解。
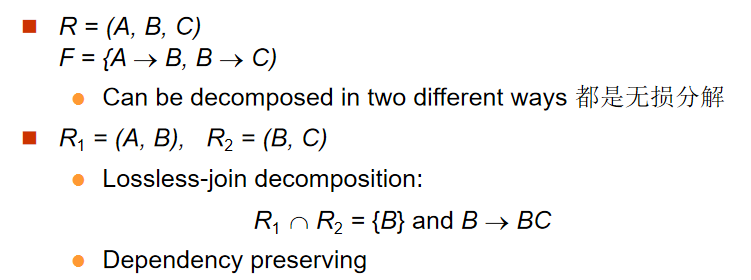
-
無損連接可能造成沒有保持依賴

-
判斷保持依賴演算法(多項式時間)

分解演算法(Decomposition Algorithm)
BCNF 分解
-
BCNF 的定義可以直接用於檢查一個關係是否屬於 BCNF。但是,計算 \(F^+\) 是一個繁重的任務。在某些情況下,判定一個關係是否屬於BCNF可以作如下簡化,只能分解之前使用:
- 為了檢查非平凡的函數依賴 α→β 是否違反 BCNF,計算 \(\alpha^+\)( α的屬性閉包),並且驗證它是否包含 R 中的所有屬性,即驗證它是否是 R 的超碼。
- 檢查關係模式 R 是否屬於 BCNF,僅須檢查給定集合 F 中的函數依賴是否違反 BCNF 就足夠了,不用檢查 \(F^+\) 中的所有函數依賴。
-
當一個關係分解後,後一步過程就不再適用。也就是說,當我們判定 R 上的一個分解 \(R_i\) 是否違反 BCNF 時,只用 \(F\) 就不夠了,只能在 \(F^+\) 的範圍。

-
BCNF 分解演算法:保證無損連接,無法保證依賴保持


🐍 實例模擬:

🔔 很多時候我們能夠得到BCNF分解,但是卻無法做到依賴保持

3NF 分解:
-
3NF 是 BCNF 的放鬆,允許一些冗餘的存在
-
3NF 分解演算法:保證無損連接,也保證依賴保持

- 先求出正則覆蓋 \(F_c\)
- 對於 \(F_c\) 裡面的所有函數依賴 a->b,均轉化為 \(R_i=ab\)
- 對於所有的模式 \(R_i\)
- 如果包含候選碼,進行第 4
- 如果都不包含候選碼, 將任意一個候選碼添加到模式 \(R_i\) 裡面
- 如果一個模式被另一個模式包含,則去掉此被包含的模式。

事務(Transactions)
事務的概念(Transaction Concept)

事物的狀態(Transaction State)
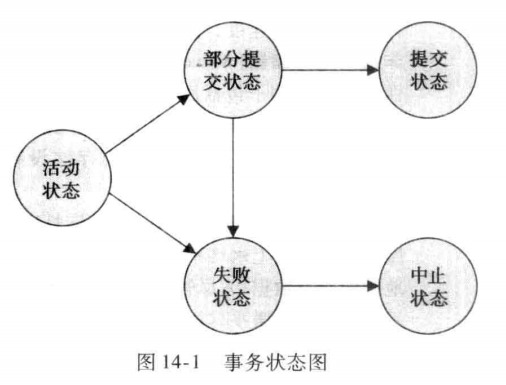
- 活動的(active):初始狀態,事務執行時處於這個狀態。
- 部分提交的(partially committed):最後一條語句執行後。
- 失敗的(failed):發現正常的執行不能繼續後。
- 中止的(aborted):事務回滾並且資料庫已恢復到事務開始執行前的狀態後。
- 提交的(committed):成功完成後。
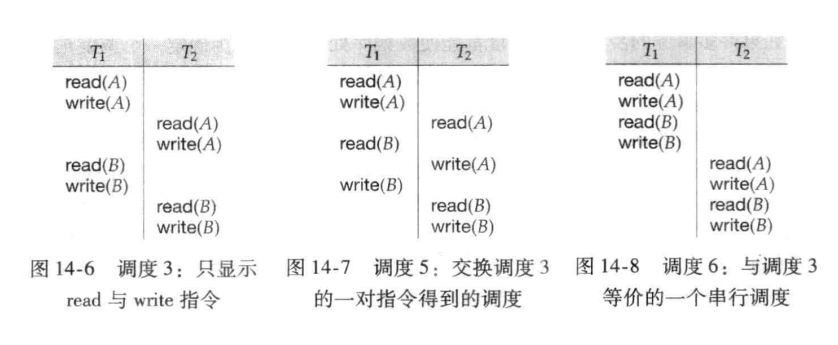
串列化(Serializability)
衝突可串列化(Conflict Serializability)
- 考慮一個調度 \(S\),其中含有分別屬於 \(I\) 與 \(J\) 的兩條連續指令 \(I_i\) 與 \(I_j\),如果 \(I\) 與 \(J\) 引用不同的數據項,則交換 \(I\)與 \(J\) 不會影響調度中任何指令的結果。
- 如果 \(I\) 與 \(J\) 引用相同的數據項,只有讀讀的時候順序無所謂,讀寫和寫寫的順序都不能變。