區間統計——ST演算法
一、引入
先舉一個小栗子。
一數組有 \(n\) 個元素,有 \(m\) 次詢問(\(n, m <= 10^5\))。對於每次詢問給出 \(l, r\),求出 \([l, r]\)的區間和。
有的同學說,這很簡單啊!直接前綴和不就行了嗎?確實如此,示例程式碼如下:
int n, m; cin >> n >> m;
vector< int > sum( n + 10 );
fill( sum.begin(), sum.end(), 0 );
for ( int i = 1, x; i <= n; ++i ) {
cin >> x;
sum[ i ] = sum[ i - 1 ] + x;
}
while ( m-- ) {
int l, r; cin >> l >> r;
l = min( l, r ); r = max( l, r );
cout << sum[ r ] - sum[ l - 1 ] << endl;
}
但是,我們稍稍改變一下題目,將求區間和改為求區間最大值,前綴和就行不通了。我們應該如何在 \(O(nlogn)\) 的時間複雜度下求得結果呢?
二、ST 演算法介紹
上面的問題也被稱為區間最值查詢。(\(RMQ\), $Range $ \(Maximum/Minimum\) \(Query\))在靜態的區間最值查詢問題中,我們可以使用 \(ST\) 演算法解決。
首先我們假定需要求解的數組為 \(A=\{ 10, 20, 30, 40, 50, 60 \}\),且為了方便,數組下標從 $ 1 $ 開始。
由於問題可離線,我們可以先預處理,再輸出答案。
基於倍增思想,我們可以對於每一個元素構造一個倍增數組,其內容為\(A\) 中 \([i, i+2^k-1]\)的最大值(\(i\in( [1,n]\cap\N), i+2^k-1\leq n, k\in \N\)),如下圖所示:
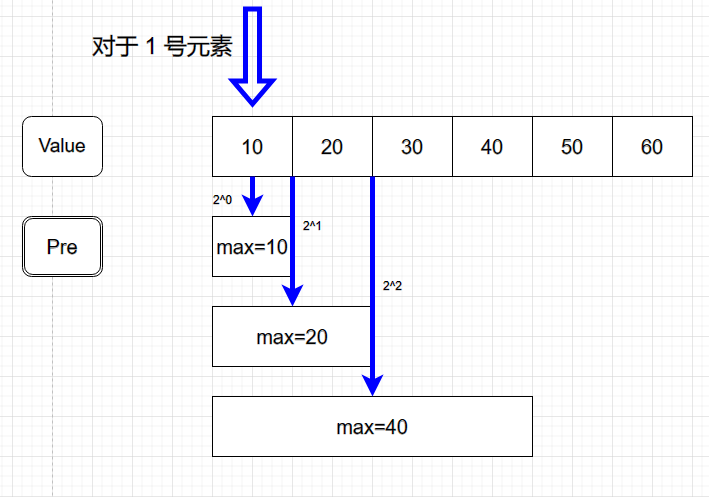
以此類推,我們可以對於每個元素構造這麼一個數組,即 \(Pre\) 數組為一個二維數組,可定義為:
int pre[ maxn ][ maxlog ]; // maxlog 為上文中 k 的最大值,一般取 25 左右
那麼,我們該如何快速求解出 \(pre[i][j]\) 呢?
三、 pre[i][j] 的求法
我們可以將 \(ST\) 演算法看作一個 DP。
首先,\(pre[i][j]\) 本身就可以視作一個狀態矩陣,存儲著對應區間的最值。
接著,其邊界條件是 \(pre[i][0]\),即元素本身。這很容易理解,因為 \([i,i]\) 的最值本身就是 \(i\) 嘛。
其次,由於預處理是離線過程,所以對於新的區間最值求解,不會對已求出區間的最值產生影響,故滿足 DP 的無後效性原則。
最後,我們來整理狀態轉移方程。
對於區間 \([i, j]\),顯然可以將其二分為 \([i, \frac{i+j}{2}]\) 和 \((\frac{i+j}{2},j)\)。若知道這兩個區間的最值 \(p\) 和 \(q\),顯然地,整個\([i,j]\)區間的最值必然等於\(max(p,q)\)或\(min(p,q)\)。這樣問題就轉化為求子區間的最值。以此類推直至邊界。我們可以結合下圖進行理解。
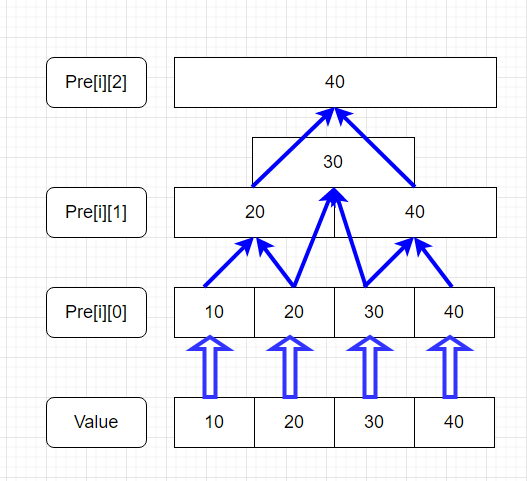
於是我們可以輕鬆寫出程式碼:
int n, m; cin >> n >> m;
for ( int i = 1; i <= n; ++i ) cin >> pre[ i ][ 0 ];
for ( int j = 1; j <= maxlog; ++j )
for ( int i = 1; i + ( 1 << j ) - 1 <= n; ++i )
pre[ i ][ j ] = max(
pre[ i ][ j - 1 ], // [i, i+2^(j-1)-1] 即前半段區間
pre[ i + ( 1 << ( j - 1 ) ) ][ j - 1 ] // [i+2^(j-1), i+2^j-1] 即後半段區間
); // 因為 2^j = 2 * 2^(j-1),所以可以這麼寫
四、How to query?
預處理完畢,該如何實現高效查詢呢?
要求的區間為 \([l, r]\),區間長度即為 \(r-l+1\)。得知了區間長度,我們就可以在 \(Pre\) 中進行查找。由於區間長度不一定為 $ 2^k, k\in N $,我們僅取一個區間返回結果不一定準確(因為 \(Pre\) 中預處理的區間長度均為 $ 2^k $)所以我們需要找到一個長度,使得其為 $ 2^k $ 且盡量長但不超過 \([l,r]\) 的長度。顯然地,這個長度為 \(floor(\log_{2}{(r-l+1)})\)。這個長度可以直接用於 \(Pre\) 且盡量大。所以所取區間為 \([l, l+2^{log_{2}{(r-l+1)}}-1]\),在 \(Pre\) 數組中即為 $ pre[l][log(r-l+1)]$。 對於 \(\complement_{[l, l+2^{log_{2}{(r-l+1)}}-1]}{[l,r]}\),由於 \(RMQ\) 問題的可重複貢獻性,我們可以找兩段重疊的區間取最值。所以可以從 \(r\) 開始向左找長度同樣為 \(floor(\log_{2}{(r-l+1)})\) 的區間,使這個區間右端點為 \(r\)。於是第二個區間為 $ [r-2^{log_{2}{(r-l+1)}}+1,r] $,對應 \(Pre\) 中即為 \(pre[r-(1<<log(r-l+1))+1][log(r-l+1)]\) 。不難發現這兩個區間的並集必為 \([l,r]\)。即兩個區間最值的 \(max/min\) 一定是整個區間的最值。通過圖片進行解釋:
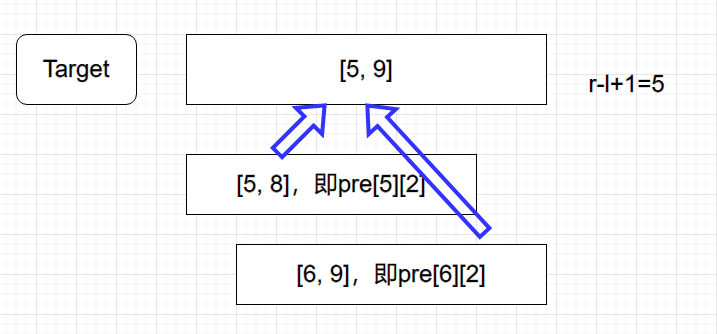
於是我們可得出 \(query\) 函數的程式碼:
inline int query( int l, int r ) {
int k = log( r - l + 1 ); // 簡化程式碼
return max(
pre[ l ][ k ],
pre[ r - ( 1 << k ) + 1 ][ k ]
);
}
下面是 \(ST\) 演算法的模板。用於解決洛谷 P3865:
#include <bits/stdc++.h>
using namespace std;
#define k lg2[r - l + 1]
typedef long long ll;
template<typename T>
inline void read(T &x) {
T f = 1; x = T(0); char ch = getchar();
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }
x *= f;
}
namespace SparseTable {
const int MAXN = 2e6 + 10, MAXLOG = 25;
int n, m, f[MAXN][MAXLOG], lg2[MAXN];
void init(void) {
// Read components
read(n); read(m);
for (int i = 1; i <= n; i++)
read(f[i][0]);
// Sparse Table
for (int j = 1; j <= MAXLOG; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1) )][ j - 1 ]);
// Log2
lg2[1] = 0; lg2[2] = 1;
for (int i = 3; i < MAXN; i++)
lg2[i] = lg2[i / 2] + 1;
}
inline int query(const int l, const int r) {
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
}
int main(void) {
int l, r;
SparseTable::init();
while ( (SparseTable::m) --) {
read(l); read(r);
printf("%d\n", SparseTable::query(min(l, r), max(l, r)));
}
return 0;
}
六、優點與局限性
\(ST\) 演算法有一些其他演算法所不具備的優點,比如:
- 程式碼量小
- 常數小,時間複雜度較低
\(ST\) 演算法的局限性很大,只能解決靜態區間可重複貢獻問題,局限性如下:
- 可擴展性較弱
- 無法處理在線修改操作
第二點實際上是 \(ST\) 表實際應用中最大的障礙。那麼,如何解決在線修改查詢問題呢?需要的兩大殺器分別是樹狀數組和線段樹(包括 zkw 線段樹),這兩種數據結構將在接下來的幾篇文章中介紹。


