論文解讀(DCN)《Towards K-means-friendly Spaces: Simultaneous Deep Learning and Clustering》
論文資訊
論文標題:Towards K-means-friendly Spaces: Simultaneous Deep Learning and Clustering
論文作者:Bo Yang, Xiao Fu, Nicholas D. Sidiropoulos, Mingyi Hong
論文來源:2016, ICML
論文地址:download
論文程式碼:download
1 Introduction
為了恢復「聚類友好」的潛在表示並更好地聚類數據,我們提出了一種聯合 DR (dimensionality reduction) 和 K-means 的聚類方法,通過學習深度神經網路(DNN)來實現 DR。
2 Background and Related Works
2.1 Kmeans
給定樣本集 $\left\{\boldsymbol{x}_{i}\right\}_{i=1, \ldots, N}$ ,$\boldsymbol{x}_{i} \in \mathbb{R}^{M}$。聚類的任務是將 $N$ 個數據樣本分成 $K$ 類。
K-Means 優化的是下述損失函數:
$\begin{array}{l}\underset{\boldsymbol{M} \in \mathbb{R}^{M \times K},\left\{\boldsymbol{s}_{i} \in \mathbb{R}^{K}\right\}}{\text{min}} \quad & \sum_{i=1}^{N}\left\|\boldsymbol{x}_{i}-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2} \\\text { s.t. } & s_{j, i} \in\{0,1\}, \mathbf{1}^{T} \boldsymbol{s}_{i}=1 \quad \forall i, j,\end{array} \quad\quad\quad(1)$
其中,
-
- $\boldsymbol{s}_{i}$ 是樣本 $x_i$ 的聚類分配向量;
- $s_{j, i}$ 是 $\boldsymbol{s}_{i}$ 的第 $j$ 個元素;
- $\boldsymbol{m}_{k}$ 代表著第 $k$ 個聚類中心;
2.2 joint DR and Clustering
考慮生成模型的數據樣本生成 $\boldsymbol{x}_{i}=\boldsymbol{W} \boldsymbol{h}_{i}$,其中 $\boldsymbol{W} \in \mathbb{R}^{M \times R}$ 、$\boldsymbol{h}_{i} \in \mathbb{R}^{R}$,並且 $R \ll M$ 。假設數據集群在潛在域中被很好地分離出來 ( $\boldsymbol{h}_{i}$)
,聯合優化問題如下:
$\begin{array}{l}\underset{\boldsymbol{M},\left\{\boldsymbol{s}_{i}\right\}, \boldsymbol{W}, \boldsymbol{H}}{\text{min }}&\|\boldsymbol{X}-\boldsymbol{W} \boldsymbol{H}\|_{F}^{2}+\lambda \sum\limits_{i=1}^{N}\left\|\boldsymbol{h}_{i}-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2} \quad+r_{1}(\boldsymbol{H})+r_{2}(\boldsymbol{W}) \\\text { s.t. } &s_{j, i} \in\{0,1\}, \mathbf{1}^{T} \boldsymbol{s}_{i}=1 \forall i, j,\end{array}$
其中,$r_1$ 和 $r_2$ 是正則化項;

3 Method
其中:
-
- $\ell(\boldsymbol{x}, \boldsymbol{y})=\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}$,同時也可以考慮 $l_1-norm$ ,或者 KL 散度;
- $f$ 和 $g$ 分別代表編碼和解碼的過程;
演算法框架:
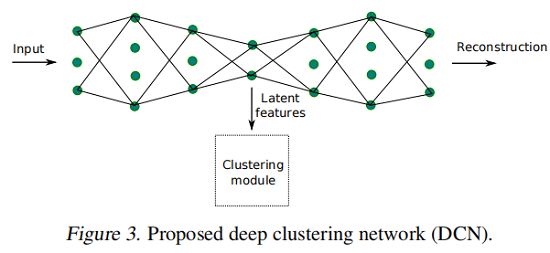
4 Optimization Procedure
4.1. Initialization via Layer-wise Pre-Training
首先通過預訓練自編碼器得到潛在表示(bottleneck layer 的輸出),然後在潛在表示上使用 K-means 得到聚類中心 $\boldsymbol{M}$ 和聚類分配向量 $s_{i}$。
4.2. Alternating Stochastic Optimization
4.2.1 Update network parameters
固定 $\left(M,\left\{s_{i}\right\}\right)$,優化 $(\mathcal{W}, \mathcal{Z})$,那麼該問題變為:
$\underset{\mathcal{W}, \mathcal{Z}}{\text{min }} L^{i}=\ell\left(\boldsymbol{g}\left(\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right), \boldsymbol{x}_{i}\right)+\frac{\lambda}{2}\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2}$
對於 $(\mathcal{W}, \mathcal{Z})$ 的更新可以藉助於反向傳播。
4.2.2 Update clustering parameters
固定網路參數和聚類質心矩陣 $M$,當前樣本的聚類分配向量 $s_i$:
$s_{j, i} \leftarrow\left\{\begin{array}{ll}1, & \text { if } j=\underset{k=\{1, \ldots, K\}}{\arg \min }\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{m}_{k}\right\|_{2}, \\0, & \text { otherwise }\end{array}\right.$
當固定 $\boldsymbol{s}_{i}$ 和 $\mathcal{X}=(\mathcal{W}, \mathcal{Z})$ 時,更新 $M$ :
$\boldsymbol{m}_{k}=\left(1 /\left|\mathcal{C}_{k}^{i}\right|\right) \sum\limits_{i \in \mathcal{C}_{k}^{i}} \boldsymbol{f}\left(\boldsymbol{x}_{i}\right)$
其中,$\mathcal{C}_{k}^{i}$ 是分配給從第一個樣本到當前樣本 $i$ 的聚類 $k$ 的樣本的記錄索引集。
雖然上面的更新是直觀的,但對於在線演算法來說可能是有問題的,因為已經出現的歷史數據(即 $\boldsymbol{x_{1}}, \ldots, \boldsymbol{x}_{i}$)可能不足以建模全局集群結構,而初始 $s_i$ 可能遠遠不正確。
因此,簡單地平均當前分配的樣本可能會導致數值問題。我們沒有做上述操作,而是使用(Sculley,2010)中的想法自適應地改變更新的學習速率來更新 $\boldsymbol{m}_{1}, \ldots, \boldsymbol{m}_{K}$。
直覺很簡單:假設 cluster 在包含的數據樣本數量上是大致是平衡的。然後,在為多個樣本更新 $M$ 之後,應該更優雅地更新已經有許多分配成員的集群的質心,同時更積極地更新其他成員,以保持平衡。為了實現這一點,讓 $c_{k}^{i}$ 是演算法在處理傳入的樣本 $x_i$ 之前分配一個樣本給集群 $k$ 的次數,並通過一個簡單的梯度步驟更新 $m_k$:
$\boldsymbol{m}_{k} \leftarrow \boldsymbol{m}_{k}-\left(1 / c_{k}^{i}\right)\left(\boldsymbol{m}_{k}-\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right) s_{k, i}\quad\quad\quad(8)$
其中,$1 / c_{k}^{i}$ 用於控制學習率。上述 $M$ 的更新也可以看作是一個SGD步驟,從而產生了在 Algorithm 1 中總結的一個整體的交替塊SGD過程。請注意,一個 epoch 對應於所有數據樣本通過網路的傳遞。

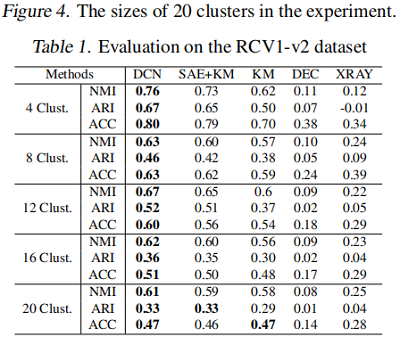
5 Experiments
聚類
6 Conclusion
在這項工作中,我們提出了一種聯合DR和K-means聚類方法,其中DR部分是通過學習一個深度神經網路來完成的。我們的目標是自動將高維數據映射到一個潛在的空間,其中K-means是一個合適的聚類工具。我們精心設計了網路結構,以避免瑣碎和無意義的解決方案,並提出了一個有效的和可擴展的優化程式來處理所制定的具有挑戰性的問題。綜合和實際數據實驗表明,該演算法在各種數據集上都非常有效。
修改歷史
2022-06-28 創建文章

