二叉搜索樹，一個簡單但是非常常見的數據結構

2022 年 6 月 2 日
筆記
演算法

前言

今天leetcode的每日一題450是關於刪除二叉搜索樹節點的，題目要求刪除指定值的節點，並且需要保證二叉搜索樹性質不變，做完之後，我覺得這道題將二叉搜索樹特性凸顯的很好，首先需要查找指定節點，然後刪除節點並且保持二叉搜索樹性質不變，就想利用這個題目講講二叉搜索樹。

二叉搜索樹作為一個經典的數據結構，具有鏈表的快速插入與刪除的特點，同時查詢效率也很優秀，所以應用十分廣泛，例如在文件系統和資料庫系統一般會採用這種數據結構進行高效率的排序與檢索操作。同時因為實現也簡單，作為一些公司演算法題入門題目也是常有的事情，所以很需要被掌握哦～♥️

所有源碼已經放在我的github中，其中包括之前實現演算法及每日一題，可以查看Data-Structures-and-Algorithms哦～

性質

二叉搜索樹或者是一棵空樹，或者是具有下列性質的一棵二叉樹，如果當前節點具有左子樹，則左子樹上的每一個節點值均小於等於當前節點值，如果當前節點具有右子樹，則右子樹上的每一個節點值均大於等於當前節點值。依據這個性質，當我們前序遍歷二叉搜索樹的時候，得到的序列應該是從小到大的非遞減序列。同時搜索指定值時，只需要與當前節點比較，根據相對大小在左子樹或者右子樹上進行搜索。

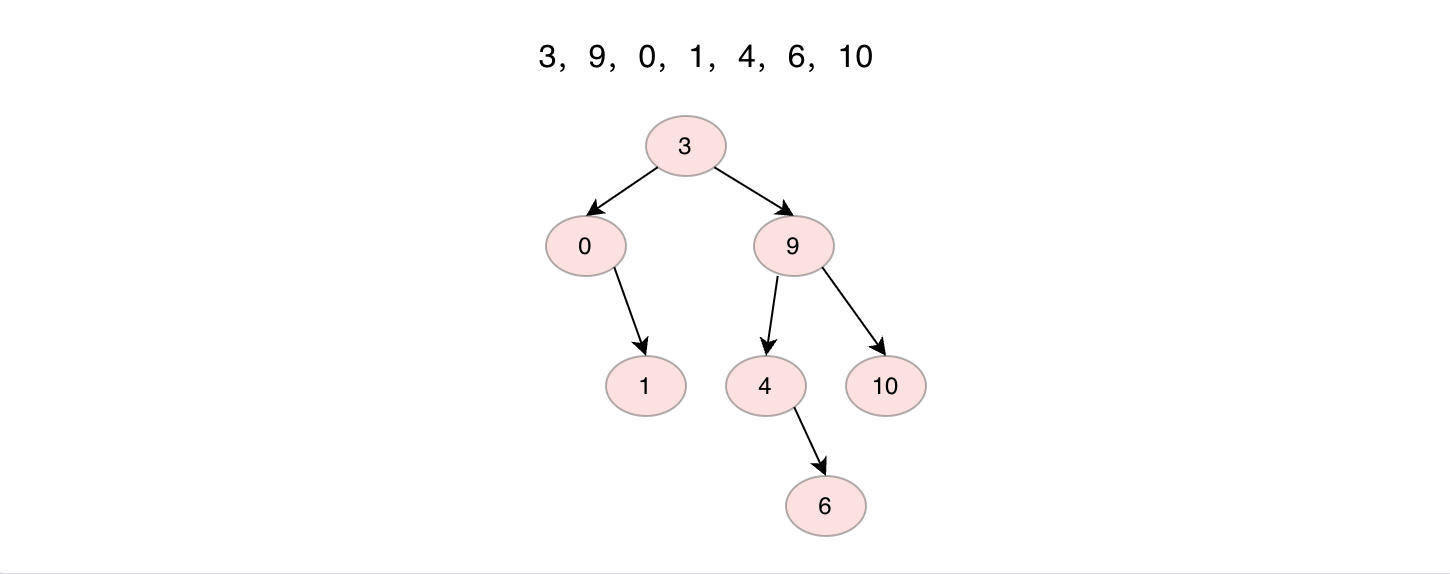
實現

根據二叉搜索樹的性質我們接下來需要實現插入節點，查詢節點，刪除節點功能。

節點結構

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode() {
    }

    public TreeNode(int val) {
        this.val = val;
    }

    public TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

初始化

這裡我們假設所有節點值大於0，初始化一個頭節點。ps：對於樹，鏈表這類數據結構，為了使第一個節點操作與其他節點保持一致，方便操作，常見的方法是添加一個額外的頭節點，指向第一個節點。

TreeNode head;
    private void init() {
        //添加一個頭節點
        head = new TreeNode(-1);
    }

插入節點

從頭節點開始我們遍歷二叉搜索樹，如果當前節點值小於等於插入節點值，則插入節點在當前節點的右子樹上，否則在左子樹上，一直深度遍歷知道當前節點的右子樹（左子樹）為空，則插入。

/**
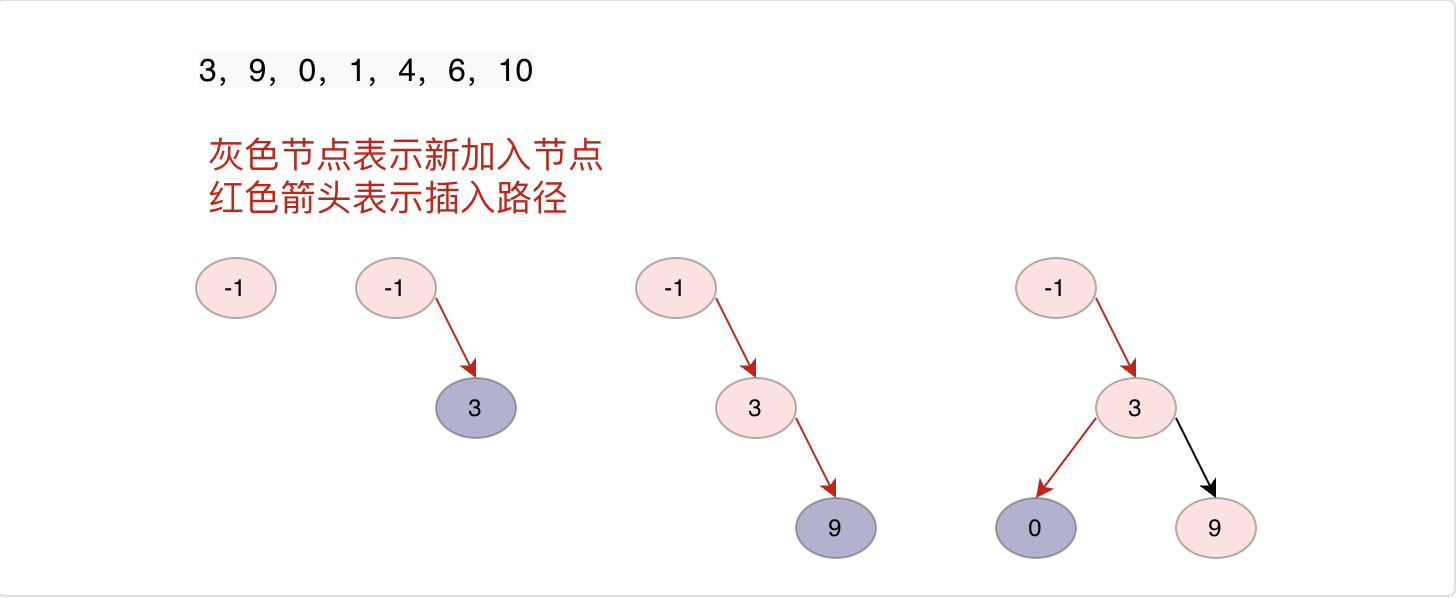
     * 插入新節點，假設新節點均大於0
     * @param val 插入節點值
     * @return 插入的節點
     */
    public TreeNode insert(int val) {
        TreeNode temp = head;
        while (true) {
            if (temp.val < val) {
                //val應該在右子樹上
                if (null != temp.right) {
                    temp = temp.right;
                    continue;
                } else {
                    temp.right = new TreeNode(val);
                    return temp.right;
                }
            }
            //應該在左子樹上
            if (null != temp.left) {
                temp = temp.left;
                continue;
            }
            temp.left = new TreeNode(val);
            return temp.left;
        }
    }

查找節點

查找節點的步驟其實在插入節點的時候已經有體現，其實就是將查找值與當前節點比較，大於當前節點走右子樹，小於當前節點走左子樹，直到值匹配返回節點，或者沒有找到返回null。ps：這裡為了後面方便實現刪除，同時返回了當前節點以及當前節點的父節點，這裡使用了commons-lang3包下的Pair工具。

/**
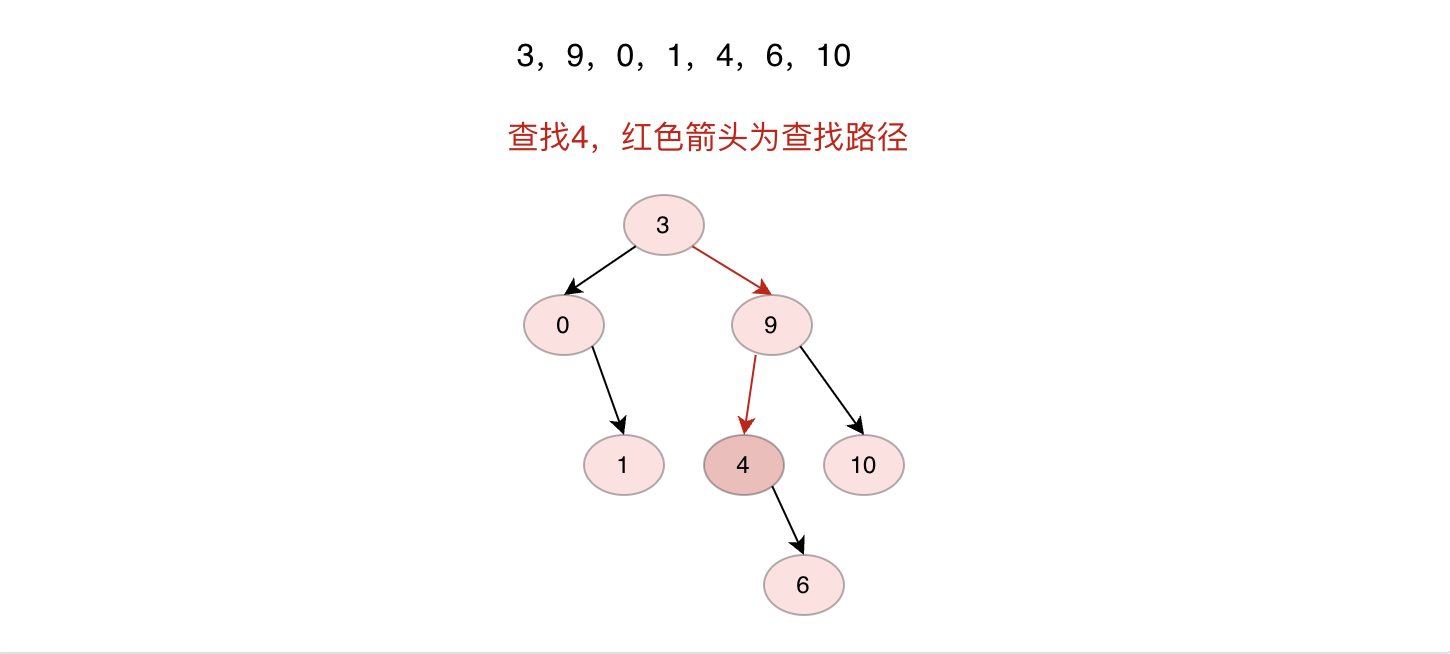
     * 搜索節點值
     * @param val
     * @return
     */
    public Pair<TreeNode, TreeNode> find(int val) {
        TreeNode temp = head.right;
        TreeNode parent = head;
        while (null != temp) {
            if (temp.val == val) {
                return Pair.of(temp, parent);
            }
            parent = temp;
            if (temp.val < val) {
                //在右子樹上
                temp = temp.right;
                continue;
            }
            temp = temp.left;
        }
        return null;
    }

刪除節點

刪除節點時候我們需要先找到刪除節點的位置，然後做對應操作。有三種情況：
1.如果刪除的是葉子節點直接刪除

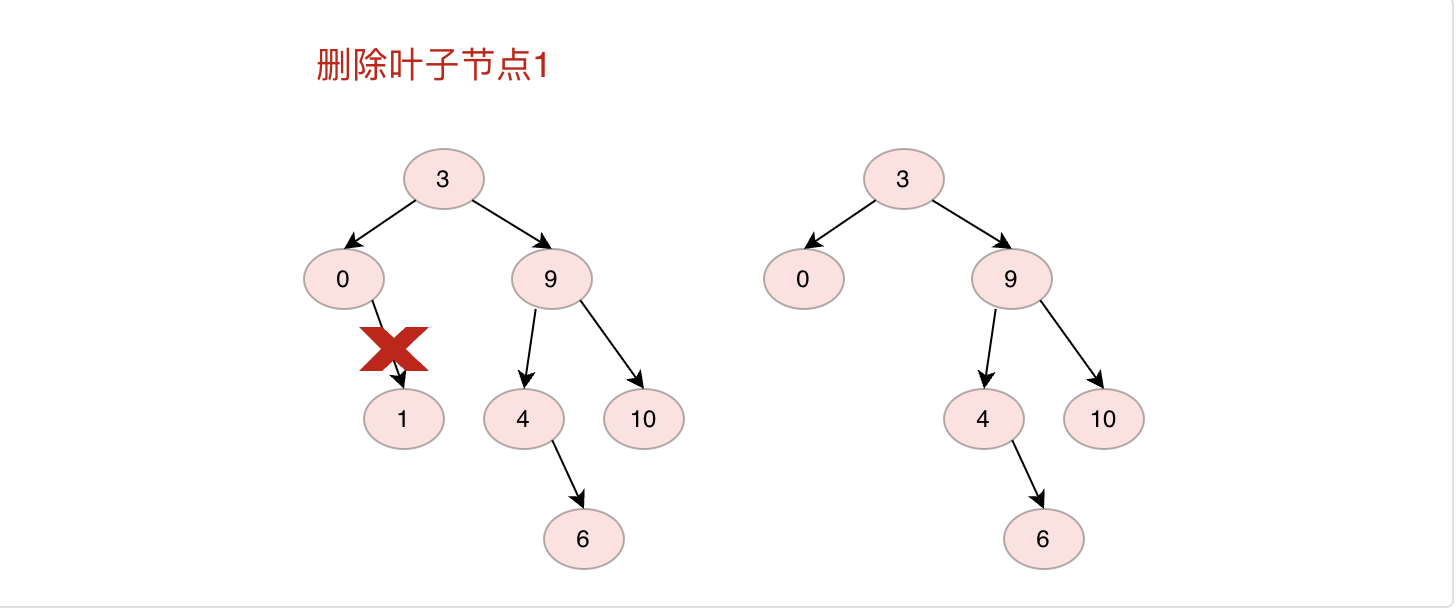
2.如果刪除的節點只有左子樹或者右子樹，則直接將左子樹或者右子樹節點放在刪除節點位置

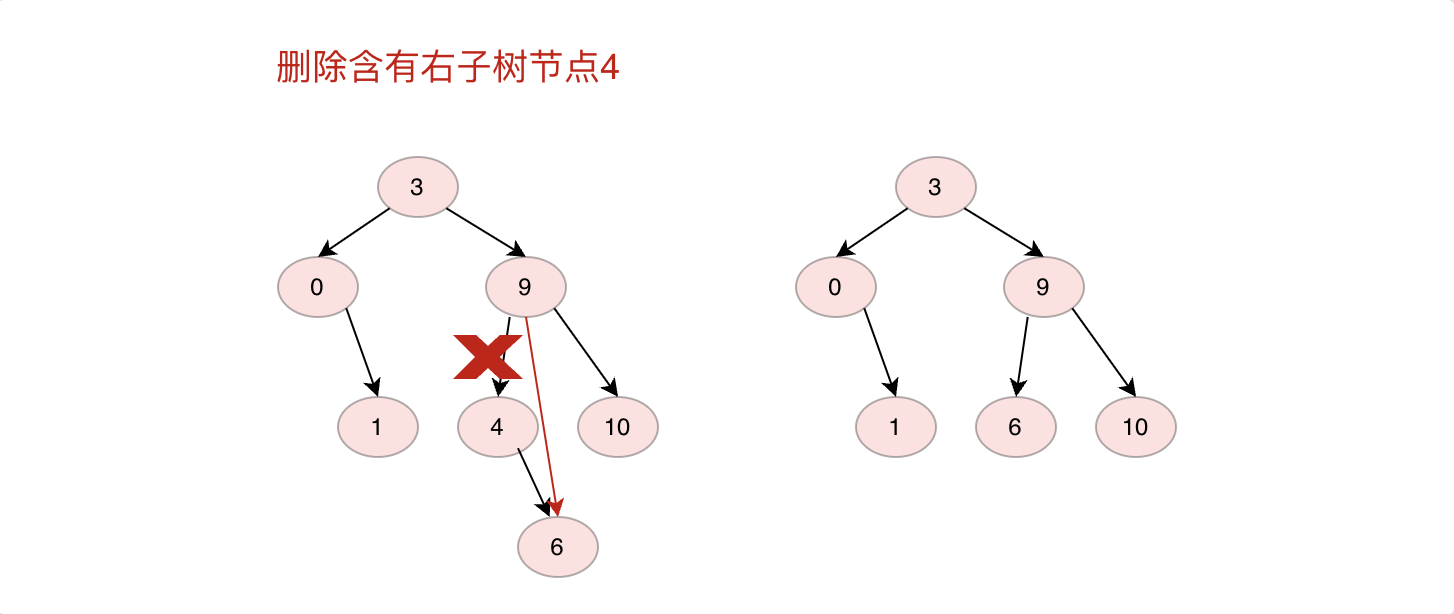
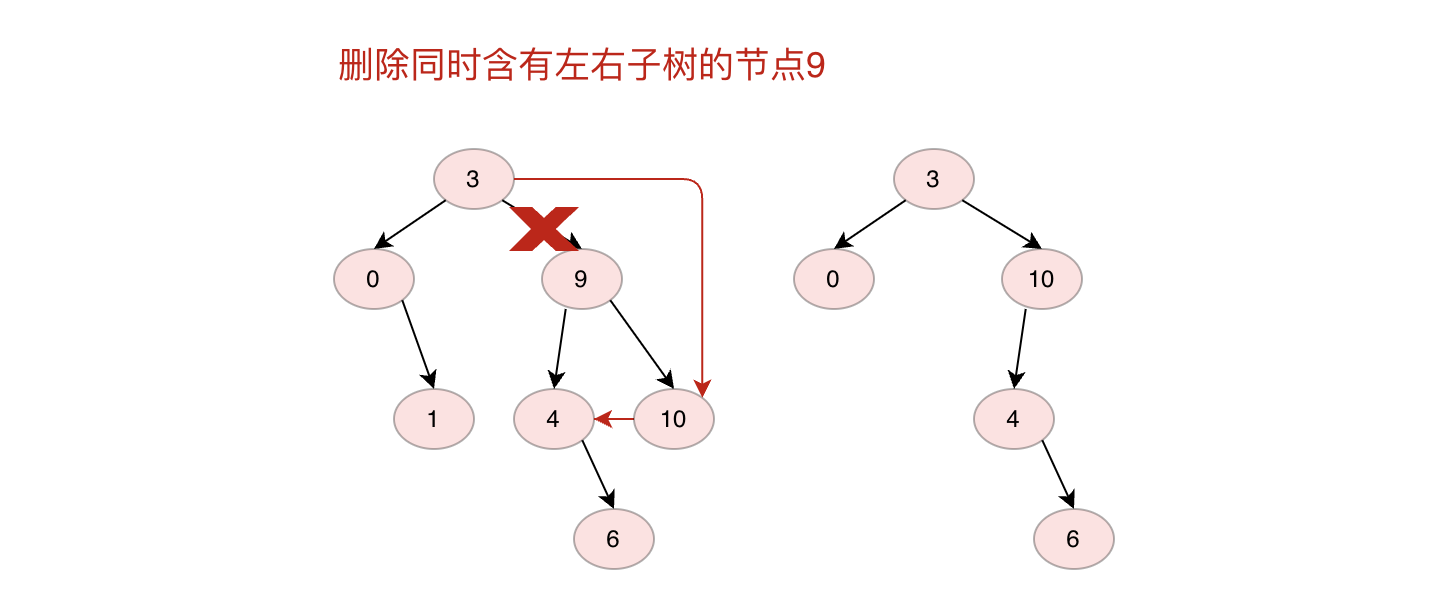
3.如果刪除節點同時有左子樹和右子樹，則將右子樹節點放在原來節點位置，將左子樹放在右子樹最左邊節點左子樹上（反之將左子樹放在原來節點位置，右子樹放在左子樹最右邊節點右子樹上也可）

/**
     * 1.如果刪除的是葉子節點直接刪除，
     * 2.如果刪除的節點只有左子樹或者右子樹，則直接將左子樹或者右子樹節點放在刪除節點位置
     * 3.如果刪除節點同時右左子樹和右子樹，則將右子樹節點放在原來節點位置，將左子樹放在右子樹最左邊節點左子樹上
     * @param val
     */
    public void delete(int val) {
        //找到刪除節點，刪除節點父節點
        Pair<TreeNode, TreeNode> curAndParent = this.find(val);
        TreeNode cur = curAndParent.getLeft();
        TreeNode parent = curAndParent.getRight();
        //記錄刪除當前節點後，當前節點位置放置哪個節點
        TreeNode changed;
        if (null == cur.left && null == cur.right) {
            changed = null;
        } else if (null != cur.left && null != cur.right) {
            TreeNode tempRight = cur.right;
            while (null != tempRight.left) {
                //找到最左側節點
                tempRight = tempRight.left;
            }
            tempRight.left = cur.left;
            changed = cur.right;
        } else if (null != cur.left) {
            changed = cur.left;
        } else {
            changed = cur.right;
        }
        if (parent.left == cur) {
            parent.left = changed;
            return;
        }
        parent.right = changed;
    }

最後

二叉搜索樹易於實現，思想簡單，被廣泛應用，平均查找，插入，刪除時間均為O(logn)，但是在刪除或者插入節點的過程中，可能因為數據的特點，使得二叉搜索樹極端情況下退化為一棵僅有左子樹或者右子樹的，這時候就跟普通順序查找無異，時間複雜度變為O(n),因此後面出現了平衡二叉搜索樹，左右子樹高度相差不超過1，通過旋轉將二叉樹高度降低，使得查找、插入、刪除在平均和最壞情況下都是O(logn)。比如常見的AVL自平衡二叉搜索樹，紅黑樹等等。

Tags: 演算法