深度學習與CV教程(2) | 影像分類與機器學習基礎

2022 年 5 月 27 日
筆記
cs231n, CV, 影像識別, 深度學習, 深度學習與電腦視覺教程 | 斯坦福CS231n · 全套筆記解讀, 線性分類, 電腦視覺

作者：韓信子@ShowMeAI
教程地址：//www.showmeai.tech/tutorials/37
本文地址：//www.showmeai.tech/article-detail/261
聲明：版權所有，轉載請聯繫平台與作者並註明出處
收藏ShowMeAI查看更多精彩內容

本系列為 斯坦福CS231n《深度學習與電腦視覺(Deep Learning for Computer Vision)》的全套學習筆記，對應的課程影片可以在這裡查看。更多資料獲取方式見文末。

引言

影像分類是電腦視覺的核心任務，電腦視覺領域中很多問題（比如 目標檢測 和 語義分割），都可以關聯到影像分類問題。影像分類 問題，就是已有固定的分類標籤集合，然後對於輸入的影像，從分類標籤集合中找出一個分類標籤，最後把分類標籤分配給該輸入影像。在本篇內容匯總，ShowMeAI將給大家講解數據驅動的模型演算法，包括簡單的 KNN 模型和 線性分類模型。

本篇重點

數據驅動方法
KNN演算法
線性分類

1.影像分類的挑戰

對於電腦而言，影像等同於一個像素矩陣；而對人類，影像是包含豐富語義資訊的多媒體呈現，對應不同的物體類別，所以對電腦而言存在巨大的語義鴻溝。

比如，給電腦輸入如下小貓的圖片，電腦影像分類模型會讀取該圖片，並計算該圖片屬於集合 $\{貓, 狗, 帽子, 杯子\}$ 中各個標籤的概率。但讀取的輸入影像數據是一個由數字組成的巨大的 $3$ 維數組。

在下圖中，貓的影像大小高 $600$ 像素，寬 $800$ 像素，有 $3$ 個顏色通道（紅、綠和藍，簡稱RGB），因此它包含了 $600 \times 800 \times 3=1440000$ 個數字，每個數字都是在範圍 $0 \sim 255$ 之間的整型，其中 $0$ 表示全黑，$255$ 表示全白。

我們的任務就是把這些數字變成一個簡單的標籤，比如「貓」。

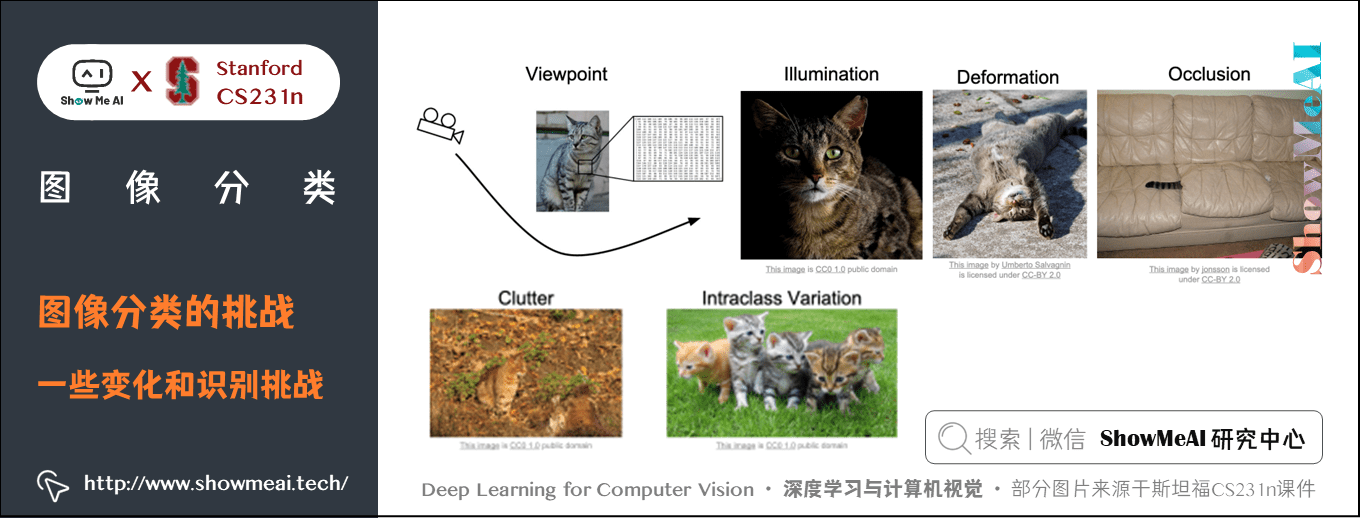
影像分類演算法要足夠健壯（魯棒，robust），我們希望它能夠適應下述變化及組合：

視角變化（Viewpoint variation）：同一個物體，攝像機可以從多個角度來展現。
大小變化（Scale variation）：物體可視的大小通常是會變化的（不僅是在圖片中，在真實世界中大小也是變化的）。
形變（Deformation）：很多東西的形狀並非一成不變，會有很大變化。
遮擋（Occlusion）：目標物體可能被擋住。有時候只有物體的一小部分（可以小到幾個像素）是可見的。
光照條件（Illumination conditions）：在像素層面上，光照的影響非常大。
背景干擾（Background clutter）：物體可能混入背景之中，使之難以被辨認。
類內差異（Intra-class variation）：一類物體的個體之間的外形差異很大，比如椅子。這一類物體有許多不同的對象，每個都有自己的外形。

如下圖所示是一些變化和影像識別的挑戰：

2.數據驅動的方式

一種實現方式是「硬編碼」：先獲取貓影像的邊緣得到一些線條，然後定義規則比如三條線交叉是耳朵之類。然而這種方式的識別效果不好，並且不能識別新的物體。

我們會採用數據驅動演算法：不具體寫出識別每個物體對應的規則，而是針對每一類物體，找到大量樣例圖片，灌給電腦進行機器學習，歸納模式規律，生成一個分類器模型，總結出區分不同類物體的核心知識要素，然後用訓練好的模型，識別新的影像。

數據驅動演算法過程如下：

輸入：輸入是包含 $N$ 個影像的集合，每個影像的標籤是 $K$ 種分類標籤中的一種。這個集合稱為訓練集。
學習：這一步的任務是使用訓練集來學習每個類的模式規律。一般該步驟叫做分類器訓練或者模型學習。
評價：讓分類器對它未曾見過的影像進行分類，把分類器預測的標籤和影像真正的分類標籤（基本事實) 對比，並以此來評價分類器的品質。

2.1 最鄰近演算法

本部分內容也可以參考ShowMeAI的 圖解機器學習教程 中的文章詳解 KNN演算法及其應用

我們這裡介紹第1個分類器演算法：最近鄰演算法。訓練過程只是簡單的記住影像數據和標籤，預測的時候和訓練數據中圖片比較找出最接近的輸出標籤。這個分類器和卷積神經網路沒有任何關係，實際中也極少使用，但通過實現它，可以對解決影像分類問題的方法有個基本認識。

1) 影像分類數據集：CIFAR-10

CIFAR-10 是一個非常流行的影像分類數據集。這個數據集包含 10 種分類標籤，60000 張 $32 \times 32$ 的小影像，每張圖片含有一個標籤。這 60000 張影像被分為包含 50000 張（每種分類 5000 張）影像的訓練集和包含 10000 張影像的測試集。

假設現在我們用這 50000 張圖片作為訓練集，將餘下的 10000 作為測試集並打上標籤，Nearest Neighbor 演算法將會拿著測試圖片和訓練集中每一張圖片去比較，然後將它認為最相似的那個訓練集圖片的標籤賦給這張測試圖片。

結果如下圖所示，效果並不是特別好。

左邊：CIFAR-10 資料庫的樣本影像；
右邊：第一列是測試影像，後面是使用Nearest Neighbor演算法，根據像素差異，從訓練集中選出的10張最類似的圖片

那麼具體如何比較兩張圖片呢？我們有一些距離度量計算方法，下面展開介紹一下。

2) L1 距離（曼哈頓距離）

距離度量的數學知識也可以參考ShowMeAI的系列教程 圖解AI數學基礎 中的文章 線性代數與矩陣論 對各種距離度量的展開講解

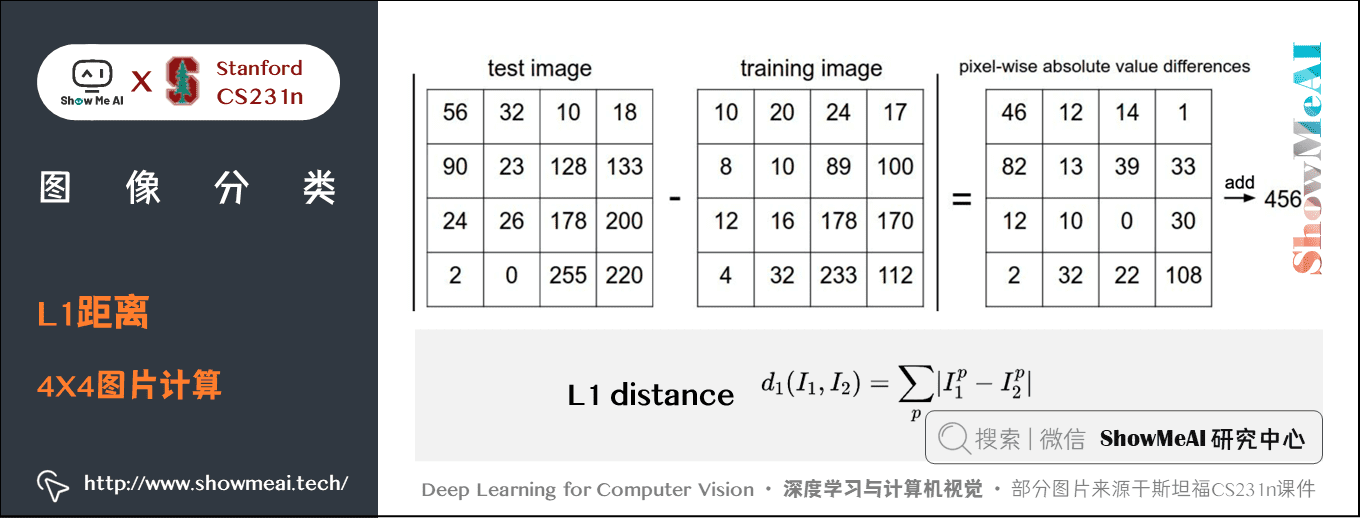
在本例中，就是比較 $32 \times 32 \times 3$ 的像素塊。最簡單的方法就是逐個像素比較，最後將差異值全部加起來。即將兩張圖片先轉化為兩個向量 $I_{1}$ 和 $I_{2}$，然後計算他們的 L1 距離：

\[d_{1} (I_{1} ,I_{2} )=\sum_{p}\vert I_{1}^p -I_{2}^p \vert
\]

其中 $p$ 為像素點，$I^p$ 表示第 $p$ 個像素點的值。
兩張圖片使用 L1 距離來進行比較，即逐個像素求差值，然後將所有差值加起來得到一個數值。如果兩張圖片一模一樣，那麼 L1 距離為 $0$；但是如果兩張圖片很是不同，那 L1 值將會非常大。

下圖是僅一個RGB通道的 $4 \times 4$ 圖片計算 L1 距離。

下面看具體編程如何實現：

① 首先，我們將 CIFAR-10 的數據載入到記憶體中，並分成4個數組：訓練數據和標籤，測試數據和標籤。

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # 這個函數可以載入CIFAR10的數據
# Xtr是一個50000x32x32x3的數組，一共50000個數據，
# 每條數據都是32行32列的數組，數組每個元素都是一個三維數組，表示RGB。
# Xte是一個10000x32x32x3的數組；
# Ytr是一個長度為50000的一維數組，Yte是一個長度為10000的一維數組。
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) 
# Xtr_rows是50000x3072的數組，按每個像素點排列，每個像素點有三個值。
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) 
# Xte_rows是10000x3072的數組
''' shape會返回數組的行和列數元組：（行數，列數），shape[0]表示行數, 
Xtr.shape[0]會返回50000；Xtr.shape會返回（50000，32，32，3）
Xtr.reshape(50000，3072)會將Xtr 重構成50000x3072數組，等於 np.reshape(Xtr, (50000,3072))'''

Xtr（大小是50000x32x32x3）存有訓練集中所有的影像
Xte（大小是10000×3072）存有測試集中所有的影像
Ytr 是對應的長度為50000的1維數組，存有影像對應的分類標籤（從0到9）
Yte 對應長度為10000的1維數組

現在我們得到所有的影像數據，每張圖片對應一個長度為 3072 的行向量。

② 接下來訓練一個分類器並評估效果。我們常常使用準確率作為評價標準，它描述了我們預測正確的得分。

本例中OK，很多其他應用中準確率並不一定是最佳的評估準則，可以參考ShowMeAI的 圖解機器學習教程 中的文章詳解 模型評估方法與準則

nn = NearestNeighbor() # 創建一個最鄰近分類器對象
nn.train(Xtr_rows, Ytr) # 用訓練圖片數據和標籤訓練分類器
Yte_predict = nn.predict(Xte_rows) # 預測測試圖片的標籤
# 並輸出預測準確率，是一個平均值
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

請注意以後我們實現的所有分類器都需要有這個介面函數（API）：train(X, y) 函數。該函數使用訓練集的數據和標籤來進行訓練。
從其內部來看，類應該實現一些關於標籤和標籤如何被預測的模型。這裡還有個 predict(X) 函數，它的作用是預測輸入的新數據的分類標籤。

下面就是使用 L1 距離的 Nearest Neighbor 分類器的實現：

import numpy as np

class NearestNeighbor(object):
  def __init__(self):
    pass

  def train(self, X, y):
    """ X 是 NxD 維的數組，每一行都是一個樣本，比如一張圖片，D 是樣本的數據維度；
    Y 是長度為 N 的一維數組。"""
    # 最鄰近分類器只是簡單的記住所有的訓練數據
    self.Xtr = X
    self.ytr = y

  def predict(self, X):
    """ X 是 NxD 維的數組，每一行都是一個希望預測其標籤的樣本 """
    num_test = X.shape[0]
    # 確保輸出的標籤數據類型和輸入的標籤格式一致，長度是測試樣本數
    Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

    # 循環所有測試樣本數，即測試數組的行數
    for i in range(num_test):
      # 為第 i 張測試圖片找到最接近的訓練圖片
      # 使用 L1 距離 (差值的絕對值求和)
      '''self.Xtr - X[i,:] 利用傳播機制，求測試集第 i 張圖片對應的行向量和
      訓練集所有圖片行向量的差值，得到一個一個50000x3072的差值矩陣；
      abs(self.Xtr - X[i,:] )會將矩陣所有元素求絕對值；
      然後axis = 1 會對差值矩陣按行求和，最終得到一個長度為50000的一維
      數組，存放第 i 張圖片和訓練集所有50000張圖片的 L1 距離。'''
      distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
      min_index = np.argmin(distances) # 獲取距離最小的訓練集圖片索引
      Ypred[i] = self.ytr[min_index] # 預測第 i 張測試集圖片的標籤時與其最接近的訓練集圖片索引

    return Ypred

這段程式碼的訓練時間複雜度為 $O(1)$，因為只是簡單的存儲數據，不管數據多大，都是一個相對固定的時間；如果訓練集有 $N$ 個樣本，則預測時間複雜度為 $O(N)$，因為測試圖片要和訓練集每張圖片進行比較。

這是一個不太好的分類器，實際對分類器的要求是，我們希望它預測的時候要快，訓練的時候可以慢。

這段程式碼跑 CIFAR-10，準確率能達到 $38.6\%$。這比隨機猜測的 $10\%$ 要好，但是比人類識別的水平和卷積神經網路能達到的 $95\%$ 還是差很多。

3) L2距離（歐式距離）

距離度量的數學知識也可以參考ShowMeAI的系列教程圖解AI數學基礎中的文章線性代數與矩陣論對各種距離度量的展開講解

另一個常用的方法是 L2 距離，從幾何學的角度，可以理解為它在計算兩個向量間的歐式距離。L2 距離的公式如下：

\[d_{2} (I_{1},I_{2})=\sqrt{\sum_{p}(I_{1}^p – I_{2}^p )^2 }
\]

依舊是在計算像素間的差值，只是先求差值的平方，然後把這些平方全部加起來，最後對這個和開方。

此時的程式碼只需改動計算距離差異的一行：

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
'''np.square(self.Xtr - X[i,:]) 會對差值矩陣的每一個元素求平方'''

注意在這裡使用了 np.sqrt，但是在實際中可能不用。因為對不同距離的絕對值求平方根雖然改變了數值大小，但依然保持了不同距離大小的順序。這個模型，正確率是 $35.4\%$，比剛才低了一點。

4) L1 和 L2比較

在 L1 距離更依賴於坐標軸的選定，坐標軸選擇不同 L1 距離也會跟著變化，判定的數據歸類的邊界會更趨向於貼近坐標系的軸來分割所屬區域，而 L2 的話相對來說與坐標系的關聯度沒那麼大，會形成一個圓，不跟隨坐標軸變化。

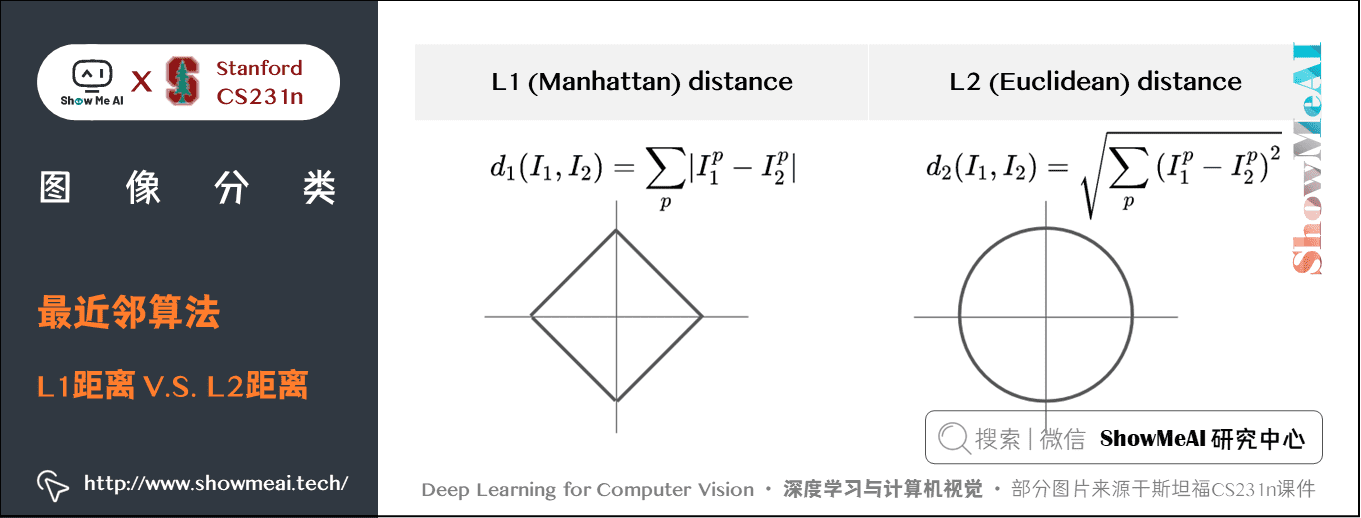
在面對兩個向量之間的差異時，L2比 L1 更加不能容忍這些差異。也就是說，相對於1個巨大的差異，L2 距離更傾向於接受多個中等程度的差異（因為會把差值平方）。

L1 和 L2 都是在 p-norm 常用的特殊形式。

當影像中有特別在意的特徵時可以選擇 L1 距離；當對影像中所有元素未知時，L2距離會更自然一些。最好的方式是兩種距離都嘗試，然後找出最好的那一個。

2.2 k最近鄰分類器

本部分內容也可以參考ShowMeAI的圖解機器學習教程中的文章詳解KNN演算法及其應用

只用最相似的 1 張圖片的標籤來作為測試影像的標籤，有時候會因為參照不夠多而效果不好，我們可以使用 k-Nearest Neighbor 分類器。KNN的思想是：找最相似的 $k$ 個圖片的標籤，$k$ 中數量最多的標籤作為對測試圖片的預測。

當 $k=1$ 的時候，k-Nearest Neighbor 分類器就是上面所說的最鄰近分類器。

如下圖所示，例子使用了2維的點來表示圖片，分成3類（紅、綠、藍）。不同顏色區域代表的是使用 L2距離的分類器的決策邊界。

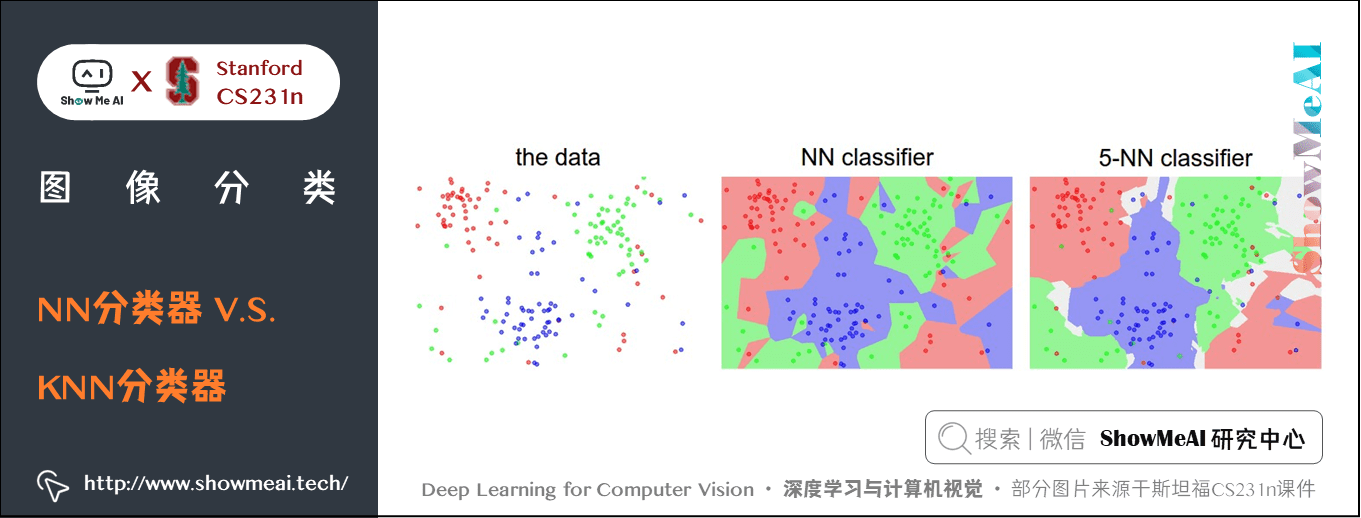
上面示例展示了NN分類器和KNN（$k=5$）分類器的區別。從直觀感受上就可以看到，更高的 $k$ 值可以讓分類的效果更平滑，使得分類器對於異常值更有抵抗力。

在 $k=1$ 時，異常的數據點（比如：在藍色區域中的綠點）製造出一個不正確預測的孤島。
在 $k=5$ 時分類器將這些不規則都平滑了，使得它針對測試數據的泛化（generalization）能力更好。
- 注意，5-NN 中也存在一些白色區域，這些區域是因為5個近鄰標籤中的最高數相同導致的分類模糊（即影像與兩個以上的分類標籤綁定）。
- 比如：2 個鄰居是紅色，2 個鄰居是藍色，還有 1 個是綠色，所以無法判定是紅色還是藍色。

1) 超參數調優

模型調優，超參數的實驗選擇方法也可以參考ShowMeAI的文章 圖解機器學習 | 模型評估方法與準則 和 深度學習教程 | 網路優化：超參數調優、正則化、批歸一化和程式框架

KNN 分類器需要設定 $k$ 值，如何選擇 $k$ 值最合適？
L1 距離和 L2 距離選哪個比較好（還是使用其他的距離度量準則例如點積）？

所有這些選擇，被稱為超參數（hyperparameter）。在基於數據進行學習的機器學習演算法設計中，超參數是很常見的。

超參數是需要提前設置的，設置完成後模型才可以訓練學習，具體的設置方法通常要藉助於實驗，嘗試不同的值，根據效果表現進行選擇。

特別注意：不能使用測試集來進行調優。

如果使用測試集來調優，而且演算法看起來效果不錯，真正的危險在於：演算法實際部署後，性能可能會遠低於預期。這種情況，稱之為演算法對測試集過擬合。

大家可以理解為，如果使用測試集來調優，實際上就是把測試集當做訓練集，由測試集訓練出來的演算法再預測測試集，性能自然會看起來很好，但實際部署起來效果就會差很多。

最終測試的時候再使用測試集，可以很好地近似度量分類器的泛化性能。

測試數據集只能使用一次，而且是在訓練完成後評價最終模型時使用，不可用來調優！

方法1：設置驗證集

從訓練集中取出一部分數據用來調優，稱之為 驗證集（validation set）。以 CIFAR-10 為例，可以用 49000 個影像作為訓練集，用 1000 個影像作為驗證集。驗證集其實就是作為假的測試集來調優。

程式碼如下：

# 假設 Xtr_rows, Ytr, Xte_rows, Yte 還是和之前一樣
# Xtr_rows 是 50,000 x 3072 的矩陣
Xval_rows = Xtr_rows[:1000, :] # 取前 1000 個訓練集樣本作為驗證集
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # 剩下的 49,000 個作為訓練集
Ytr = Ytr[1000:]

# 找出在驗證集表現最好的超參數 k 
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
  # 使用一個明確的 k 值評估驗證集
  nn = NearestNeighbor()
  nn.train(Xtr_rows, Ytr)
  # 這裡假設一個修正過的 NearestNeighbor 類，可以把 k 值作為參數輸入
  Yval_predict = nn.predict(Xval_rows, k = k)
  acc = np.mean(Yval_predict == Yval)
  print 'accuracy: %f' % (acc,)

  # 把每個 k 值和相應的準確率保存起來
  validation_accuracies.append((k, acc))

程式結束後，作圖分析出哪個 $k$ 值表現最好，然後用這個 $k$ 值來跑真正的測試集，並作出對演算法的評價。

方法2：交叉驗證

訓練集數量較小（因此驗證集的數量更小）時，可以使用交叉驗證的方法。還是用剛才的例子，如果是交叉驗證集，我們就不是取 1000 個影像，而是將訓練集平均分成 5 份，每份 10000 張圖片，其中4份用來訓練，1份用來驗證。然後我們循環著取其中4份來訓練，其中1份來驗證，最後取所有5次驗證結果的平均值作為演算法驗證結果。

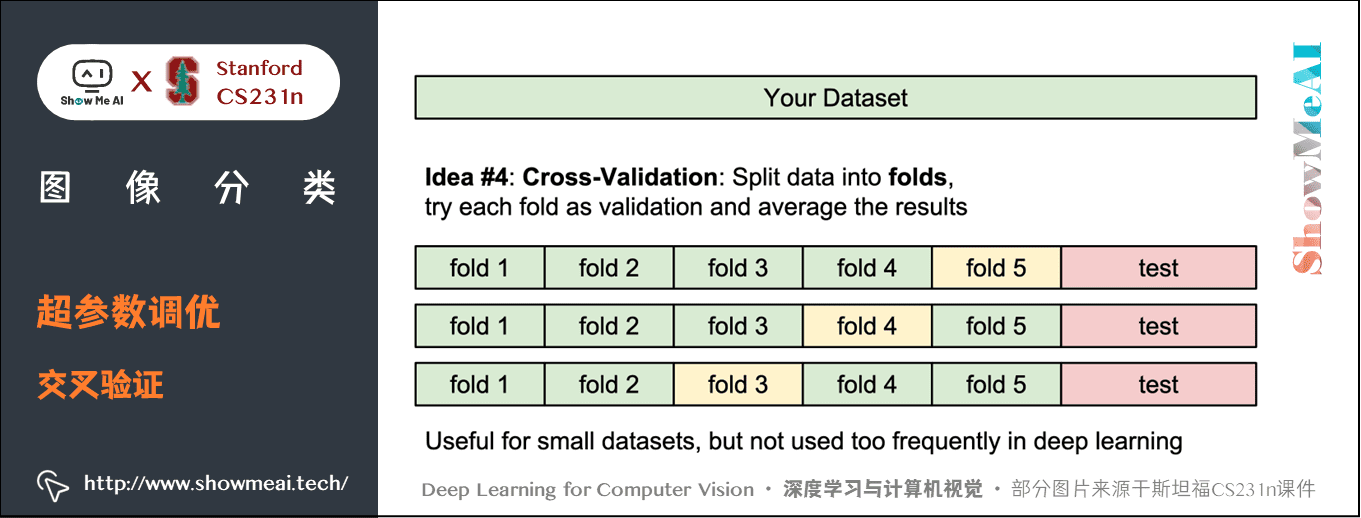
下面是 5 份交叉驗證對 $k$ 值調優的例子。針對每個 $k$ 值，得到 5 次驗證的準確率結果，取其平均值，然後對不同 $k$ 值的平均表現畫線連接。

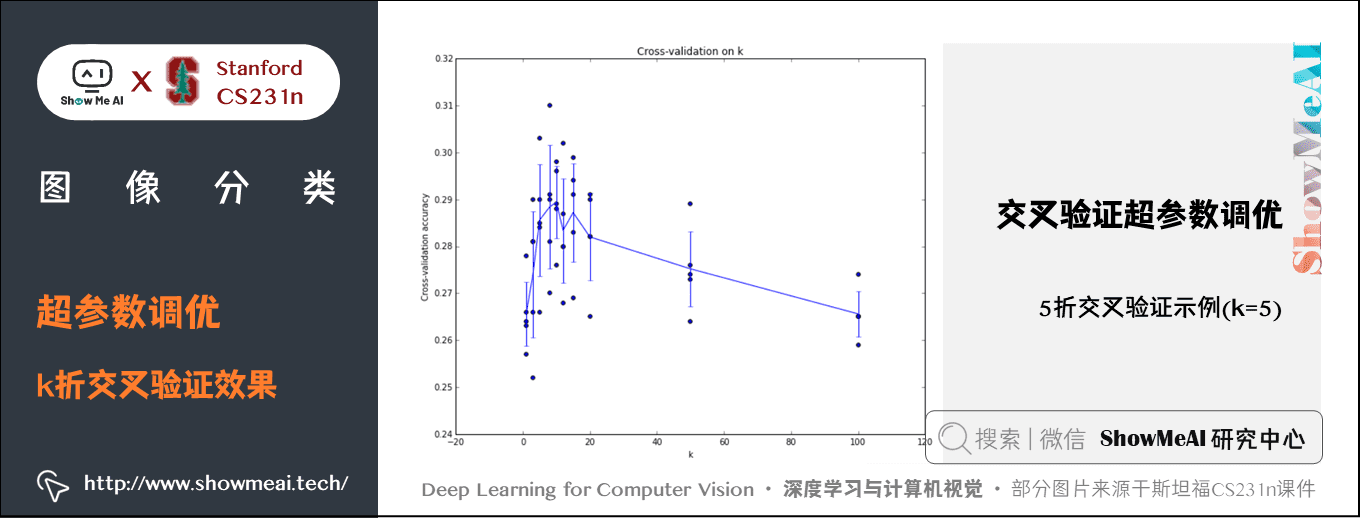
上圖可以看出，本例中，當 $k=7$ 的時演算法表現最好（對應圖中的準確率峰值）。如果我們將訓練集分成更多份數，直線一般會更加平滑（噪音更少）。

實際情況下，深度學習不會使用交叉驗證，主要是因為它會耗費較多的計算資源。一般直接把訓練集按照 $50\% \sim 90\%$ 的比例分成訓練集和驗證集。但是訓練集數量不多時可以使用交叉驗證，一般都是分成3、5和10份。

2) KNN分類器優點

① 易於理解，實現簡單。
② 演算法的訓練不需要花時間，因為其訓練過程只是將訓練集數據存儲起來。

3) KNN分類器缺點

① 測試要花費大量時間

因為每個測試影像需要和所有存儲的訓練影像進行比較在實際應用中，關注測試效率遠遠高於訓練效率；

② 使用像素差異來比較影像是不夠的，圖片間 L2 距離小，更多的是被背景主導而不是圖片語義內容本身主導，往往背景相似圖片的 L2 距離就會小。

也就是說，在高維度數據上，基於像素的相似和基於感官上的相似非常不同。感官上不同的兩張圖片，可能有相同的 L2 距離。

③ 維度災難

KNN 有點像訓練數據把樣本空間分成幾塊，我們需要訓練數據密集的分布在樣本空間里，否則測試圖片的最鄰近點可能實際距離會非常遠，導致和最接近的訓練集樣本實際上完全不同。但是如果使訓練數據密集分布，需要的訓練集數量指數倍增加，是數據維度的平方。

4) 實際應用KNN

下面是一些對於實際應用 KNN 演算法的建議

① 預處理數據

對數據中的特徵進行歸一化（normalize），讓其具有零均值（zero mean）和單位方差（unit variance）。本小節不討論，是因為影像中的像素都是同質的，不會表現出較大的差異分布，不需要標準化處理。

② 降維

如果數據是高維數據，考慮使用降維方法，比如 PCA 或者隨機投影。

③ 將數據隨機分入訓練集和驗證集

一般規律，$70\% \sim 90\%$ 數據作為訓練集。這個比例根據演算法中有多少超參數，以及這些超參數對於演算法的預期影響來決定。
如果需要預測的超參數很多，那麼就應該使用更大的驗證集來有效地估計它們；如果擔心驗證集數量不夠，那麼就嘗試交叉驗證方法；如果計算資源足夠，使用交叉驗證更好（份數越多，效果越好，也更耗費計算資源）。

④ 在驗證集上調優

嘗試足夠多的 $k$ 值，嘗試 L1 和 L2 兩種範數計算方式。

⑤ 加速分類器

如果分類器跑得太慢，嘗試使用ANN庫（比如 FLANN 來加速這個過程，其代價是降低一些準確率。

⑥ 對最優的超參數做記錄

記錄最優參數後，不要使用最優參數的演算法在完整的訓練集上運行並再次訓練，這樣做會破壞對於最優參數的估計。
直接使用測試集來測試用最優參數設置好的最優模型，得到測試集數據的分類準確率，並以此作為你的KNN分類器在該數據上的性能表現。

3.線性分類：評分函數

3.1 線性分類概述

KNN 模型中訓練過程中沒有使用任何參數，只是單純的把訓練數據存儲起來（參數 k 是在預測中使用的，找出 $k$ 個接近的圖片，然後找出標籤最多的，並且 $k$ 是超參數，是人為設定的）。

與之相對的是參數模型，參數模型往往會在訓練完成後得到一組參數，之後就可以完全扔掉訓練數據，預測的時候只需和這組參數做某種運算，即可根據運算結果做出判斷。線性分類器是參數模型里最簡單的一種，但卻是神經網路里很重要的基礎模組。

線性分類的方法由兩部分組成：

① 評分函數（score function）

它是原始影像數據到類別分值的映射。

② 損失函數（loss function）

它用來量化評分函數計算的分數與真實標籤之間的一致性。該方法可轉化為一個最優化問題，在最優化過程中，通過更新評分函數的參數來最小化損失函數值。

3.2 評分函數

評分函數將影像的像素值映射為各個分類類別的得分，得分高低代表影像屬於該類別的可能性高低。上面的所有說明都比較抽象，下面以具體的例子說明。

重新回到 KNN 使用的 CIFAR-10 影像分類數據集。

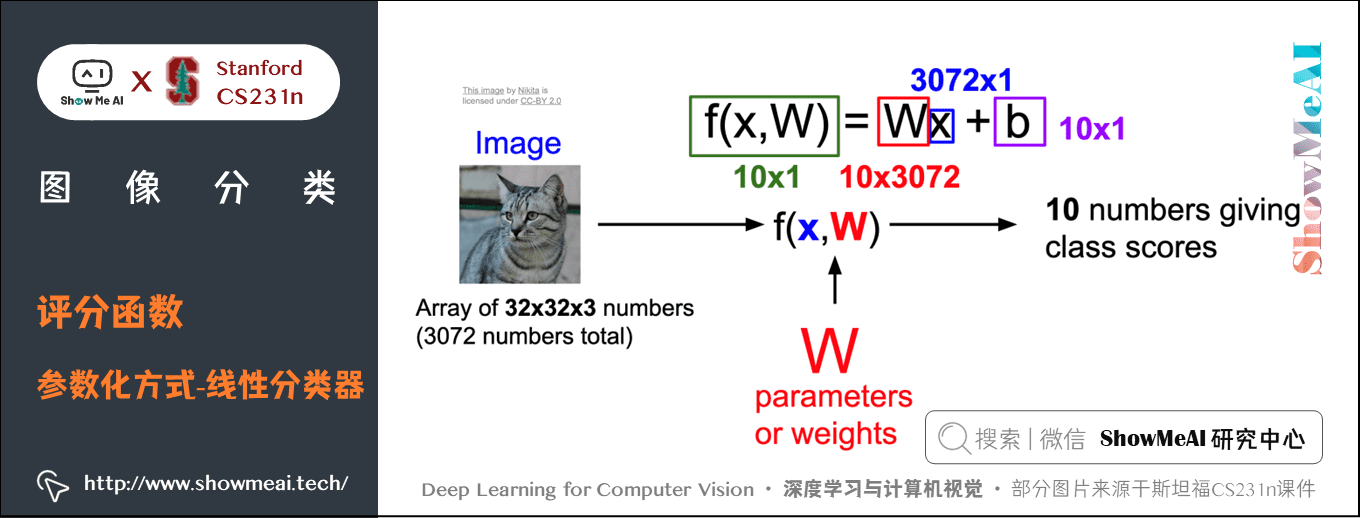
假設我們的訓練集有 $N$ 個樣本，這裡 $N=50000$，每個樣本 $x_{i}b \in R^D$，其中 $i = 1,2,\cdots,N$，$D=3072$；每個 $x_{i}$ 對應著一個標籤 $y_{i}$，$ y_{i}$ 在 $[1, K]$ 上取值，$K$ 表示總分類數，這裡 $K=10$。現在可以定義評分函數： $f:R^D \rightarrow R^K$，即把一個 $D$ 維的影像映射為 $K$ 個類別的分數。

最簡單的模型是線性模型：參數和輸入數據相乘。即：

\[f(x_{i},W,b)=Wx_{i}+b
\]

上式中參數 $W$ 被稱為權重，$b$ 被稱為偏置項
在上面的公式中，假設每個影像數據都被拉長為一個長度為 $D$ 的列向量，大小為 $[D \times 1]$。其中大小為 $[K \times D]$ 的矩陣 $W$ 和大小為 $[K \times 1]$ 的列向量 $b$ 為該函數的參數（parameters）。

還是以 CIFAR-10 為例，$x_{i}$ 就包含了第 $i$ 個影像的所有像素資訊，這些資訊被拉成為一個 $[3072 \times 1]$ 的列向量，$W$ 大小為 $[10 \times 3072]$，$b$ 的大小為 $[10 \times 1]$。因此，輸入 $3072$ 個數字（原始像素數值），函數輸出 $10$ 個數字（不同分類得到的分值），是一個 $3072$ 維到 $10$ 維的映射。

注意：

常常混用權重（weights）和參數（parameters）這兩個術語，實際上數據和參數相乘，就相當於數據占的比重，這個權重就是參數值；
該方法的一個優勢是訓練數據是用來學習參數 $W$ 和 $b$ 的，一旦訓練完成，訓練數據就可以丟棄，留下學習到的參數即可。當測試影像時可以簡單地把影像數據輸入給函數，函數計算出的分類分值來進行分類；
輸入數據 $(x_{i},y_{i})$ 是給定且不可改變的，但參數 $W$ 和 $b$ 是可改變的。目標就是通過改變這些參數，使得計算出來的分類分值情況和訓練集中影像數據的真實類別標籤相符；
只需一個矩陣乘法和一個矩陣加法就能對一個測試數據分類，這比 KNN 中將測試影像和所有訓練數據做比較的方法要高效很多。

3.3 理解線性分類器

1) 理解一：W是所有分類器的組合

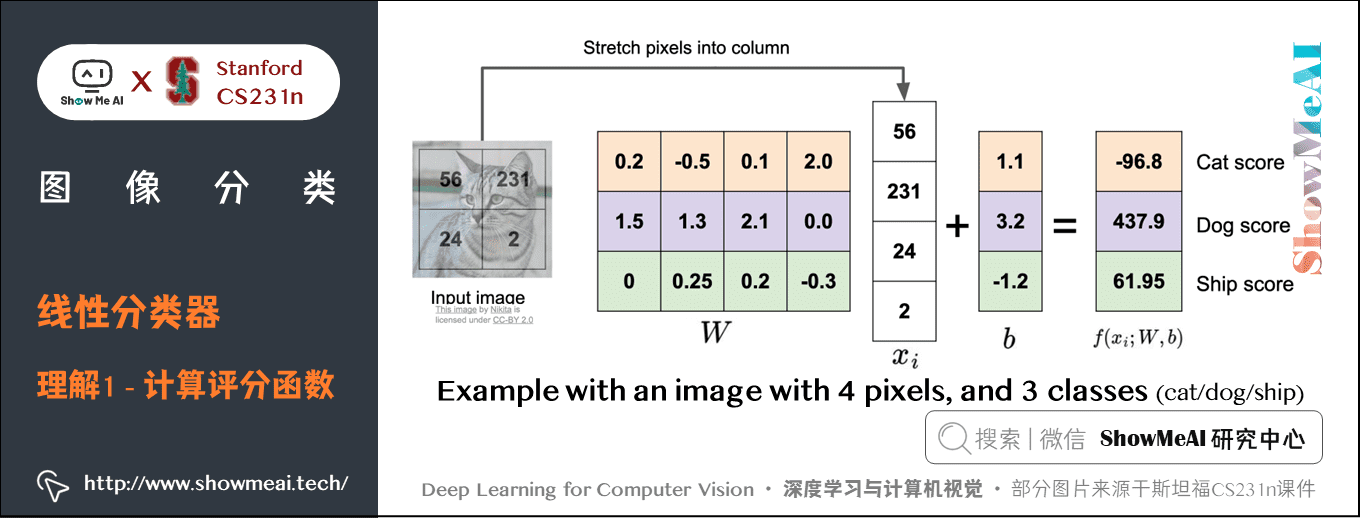
如上圖所示，將小貓的影像像素數據拉伸成一個列向量 $x_i$，這裡為方便說明，假設影像只有4個像素（都是黑白像素，不考慮RGB通道），即 $D=4$；有 $3$ 個分類（紅色代表貓，綠色代表狗，藍色代表船，顏色僅代表不同類別，和 RGB 通道沒有關係），即 $K=3$。$W$ 矩陣乘列向量 $x_i$，得到各個分類的分值。

實際上，我們可以看到，參數矩陣 $W$ 相當於是三個分類器的組合，$W$ 的每一行都是一個分類器，分別對應貓、狗、船。在線性模型中每個分類器的參數個數與輸入影像的維度相當，每個像素和對應的參數相乘，就表示該像素在該分類器中應占的比重。

需要注意的是，這個 $W$ 一點也不好：貓分類的分值非常低。從上圖來看，演算法倒是覺得這個影像是一隻狗。

我們可以這樣理解，線性分類器會計算影像中 3 個顏色通道中所有像素的值與權重矩陣的乘積，進而得到每個類別分值。根據我們對權重設置的值，對於影像中的某些位置的某些顏色，函數表現出喜好或者厭惡（根據每個權重的符號而定）。

舉例：可以想像「船」分類就是被大量的藍色所包圍（對應的就是水）。那麼「船」分類器在藍色通道上的權重就有很多的正權重（它們的出現提高了「船」分類的分值），而在綠色和紅色通道上的權重為負的就比較多（它們的出現降低了「船」分類的分值）。

結合上面的小貓示例，貓分類器對第二個位置的像素比較「厭惡」，而恰好輸入的小貓影像第二個位置像素值很大，最終計算得到一個很低的分數（當然，這個分類器是錯誤的）。

2) 理解二：將線性分類器看做模板匹配

把權重 $W$ 的每一行看作一個分類的模板，一張影像對應不同分類的得分，是通過使用內積（也叫點積）來比較影像和模板，然後找到和哪個模板最相似。

這種理解角度下，線性分類器在利用學習到的模板，和輸入影像做模板匹配。我們設置可以把其視作一種高效的KNN，不同的是不再使用所有的訓練集的影像來比較，而是每個類別只用了一張圖片來表徵（這張圖片是我們學習到的模板，而不存在訓練集中），而且我們會更換度量標準，使用（負）內積來計算向量間的距離，而不是使用 L1 或者 L2 距離。

上圖是以 CIFAR-10 為訓練集，學習結束後的權重的例子。可以看到：

馬的模板看起來似乎是兩個頭的馬，這是因為訓練集中的馬的影像中馬頭朝向各有左右造成的。線性分類器將這兩種情況融合到一起了；
汽車的模板看起來也是將幾個不同的模型融合到了一個模板中，這個模板上的車是紅色的，是因為 CIFAR-10 中訓練集的車大多是紅色的。線性分類器對於不同顏色的車的分類能力是很弱的，但是後面可以看到神經網路是可以完成這一任務的；
船的模板如期望的那樣有很多藍色像素。如果影像是一艘船行駛在大海上，那麼這個模板利用內積計算影像將給出很高的分數。

3) 理解三：將影像看做高維空間的點

既然定義每個分類類別的分值是權重和影像的矩陣乘積，那麼每個分類類別的分數就是這個空間中的一個線性函數的函數值。我們沒辦法可視化 $3072$ 維空間中的線性函數，但假設把這些維度擠壓到二維，那麼就可以看看這些分類器在做什麼了：

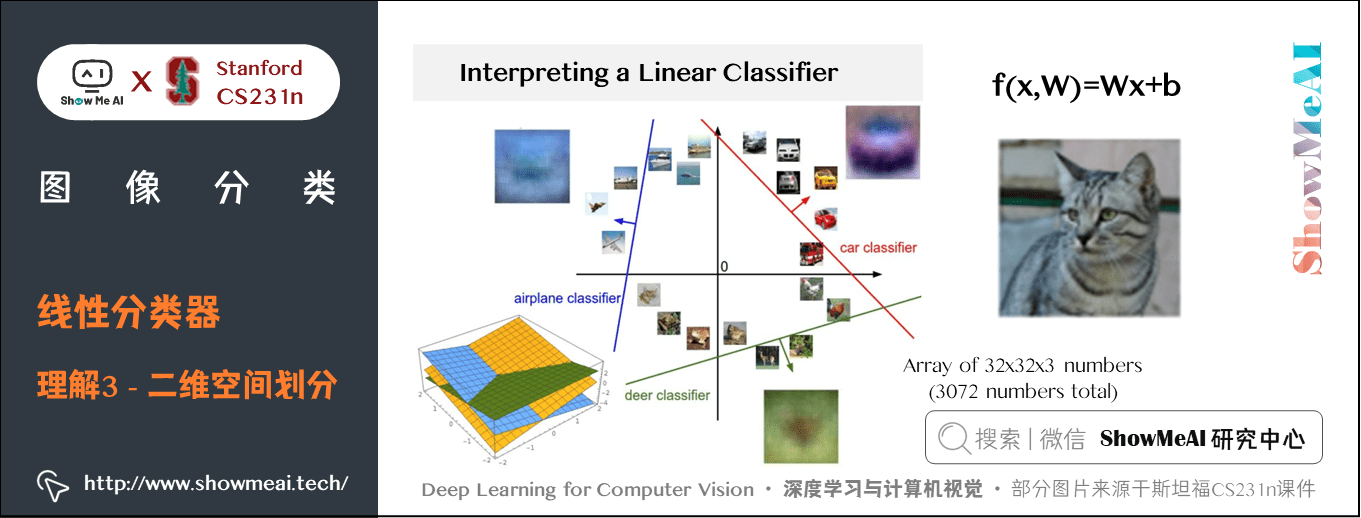
在上圖中，每張輸入圖片是一個點，不同顏色的線代表 3 個不同的分類器。以紅色的汽車分類器為例，紅線表示空間中汽車分類分數為 $0$ 的點的集合，紅色的箭頭表示分值上升的方向。所有紅線右邊的點的分數值均為正，且線性升高。紅線左邊的點分值為負，且線性降低。

從上面可以看到，$W$ 的每一行都是一個分類類別的分類器。對於這些數字的幾何解釋是：

如果改變 $W$ 一行的數字取值，會看見分類器在空間中對應的直線開始向著不同方向旋轉。而偏置項 $b$，則允許分類器對應的直線平移。
需要注意的是，如果沒有偏置項，無論權重如何，在 $x_{i}=0$ 時分類分值始終為 $0$。這樣所有分類器的線都不得不穿過原點。

3.4 偏置項和權重合併

上面的推導過程大家可以看到：實際我們有權重參數 $W$ 和偏置項參數 $b$兩個參數，分開處理比較冗餘，常用的優化方法是把兩個參數放到同一個矩陣中，同時列向量 $x_{i}$ 就要增加一個維度，這個維度的數值是常量 $1$，這就是默認的偏置項維度。

如下圖所示，新的公式就簡化成如下形式：

\[f(x_{i},W,b)=Wx_{i}
\]

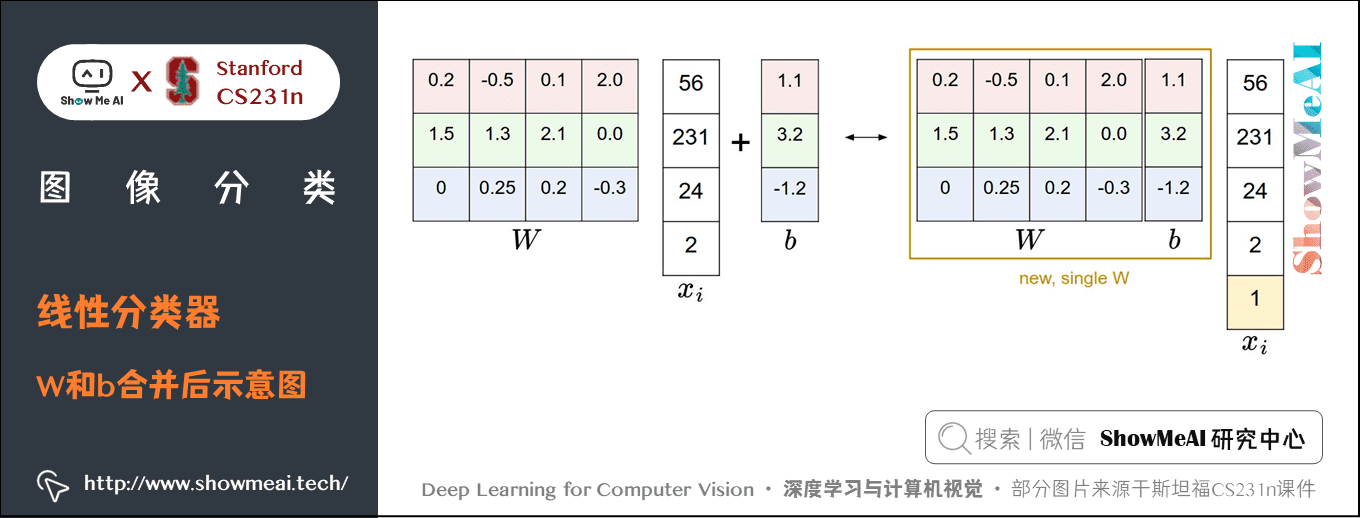
還是以 CIFAR-10 為例，那麼 $x_{i}$ 的大小就變成 $[3073 \times 1]$，而不是 $[3072 \times 1]$ 了，多出了包含常量1的1個維度； $W$ 大小就是 $[10 \times 3073]$ 了，$W$ 中多出來的這一列對應的就是偏差值 $b$：

經過這樣的處理，最終只需學習一個權重矩陣，無需學習兩個分別裝著權重和偏差的矩陣。

3.5 影像數據預處理

在上面的例子中，所有影像都是使用的原始像素值（$0 \sim 255$）。在機器學習中，我們經常會對輸入的特徵做歸一化（normalization）處理，對應到影像分類的例子中，影像上的每個像素可以看做一個特徵。

在實踐中，我們會有對每個特徵減去平均值來中心化數據這樣一個步驟。

在這些圖片的例子中，該步驟是根據訓練集中所有的影像計算出一個平均影像值，然後每個影像都減去這個平均值，這樣影像的像素值就大約分布在 $[-127, 127]$ 之間了。

後續可以操作的步驟包括歸一化，即讓所有數值分布的區間變為 $[-1, 1]$。

3.6 線性分類器失效的情形

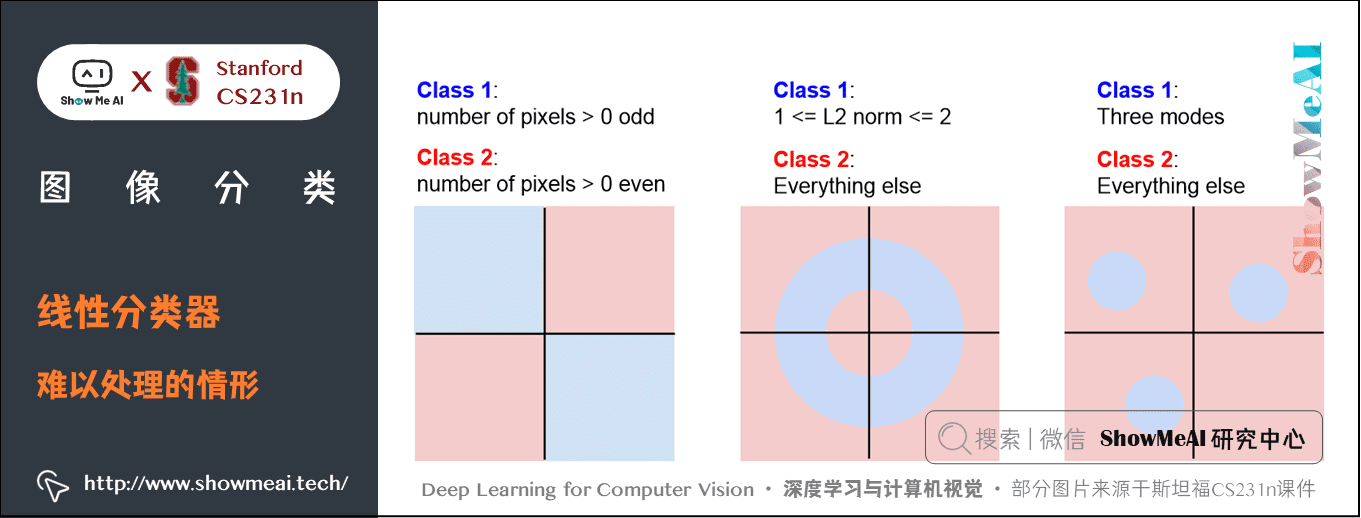
線性分類器的分類能力實際是有限的，例如上圖中的這三種情形都無法找到合適的直線區分開。其中第 1 個 case 是奇偶分類，第 3 個 case 是有多個模型。

4.拓展學習

可以點擊 B站查看影片的【雙語字幕】版本

5.要點總結

影像分類中的困難與挑戰
數據驅動方法、最鄰近演算法、 L1 和 L2 距離
KNN分類器、超參數調優、KNN的優缺點與實際應用
線性分類的概念、評分函數的理解、參數合併、數據預處理、線性分類器局限性