論文解讀(ClusterSCL)《ClusterSCL: Cluster-Aware Supervised Contrastive Learning on Graphs》
論文資訊
論文標題:ClusterSCL: Cluster-Aware Supervised Contrastive Learning on Graphs
論文作者:Yanling Wang, Jing Zhang, Haoyang Li, Yuxiao Dong, Hongzhi Yin, Cuiping Li
論文來源:2020, ICML
論文地址:download
論文程式碼:download
1 Introduction
圖上的監督對比學習很難處理擁有較大的類內(intra-class)差異,類間(inter-class)相似性的數據集。
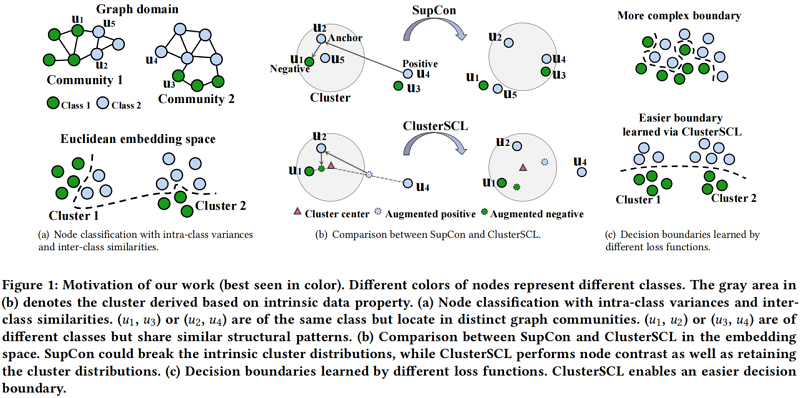
Figure 1(a) 頂部中 $(u_1,u_3)$ 、$(u_2,u_4)$ 屬於同一個類,但在不同的圖社區(intra-class variances),而 $(u_1,u_2)$、$(u_3,u_4)$ 來自不同的類但在同一圖社區(inter-class similarities)。針對上述問題,需要找出一個複雜的決策邊界,見 Figure 1(a) 底部。
當執行自監督對比(SupCon)為 $u_{2}$ 尋找錨節點,如 Figure 1(b) 所示,正樣本對屬於同一類但位於不同的簇,如 $\left(u_{2}, u_{4}\right)$。簡單地把正對(相同標籤節點)放在同一嵌入空間,可能間接把不同類的節點,如 $\left(u_{2}, u_{3}\right)$ 看成正對,因為 $u_{3}$ 和 $u_{4}$ 社區結構類似。同時,對屬於不同類但位於同一簇中的負樣本對,如 $\left(u_{2}, u_{1}\right)$,簡單地把它們推開可能間接推開同一類的節點,如 $\left(u_{2}, u_{5}\right)$,因為 $u_{5}$ 在結構上與 $u_{1}$ 相似。
上述問題總結為:簡單的執行類內差異小,類間方差大的思想,可能會造成分類錯誤,導致 Figure 1(c) 頂部顯示的更複雜的決策邊界。
本文的想法簡單的如 Figure 1(b) 底部所示。
2 Method
2.1 Base CL Scheme: SupCon
對一個 batch 內的節點 $v_{i}$ ,其正樣本下標集合 $S_{i}$,$s_{i} \in S_{i}$ 是 $v_{i}$ 正樣本的索引。SupCon 損失函數如下:
${\large \mathcal{L}_{\text {SupCon }}=-\sum\limits _{v_{i} \in B} \frac{1}{\left|S_{i}\right|} \sum\limits _{s_{i} \in S_{i}} \log \frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{s_{i}} / \tau\right)}{\sum\limits _{v_{j} \in B \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j} / \tau\right)}} \quad\quad\quad(3)$
其中 $\mathbf{h}$ 代表著經 $\ell_{2}$-normalized 處理後的表示。
2.2 Proposed CL Scheme: ClusterSCL
假設 SupCon 學習過程中有 $M$ 個潛在簇,引入潛在變數 $c_{i} \in\{1,2, \ldots, M\}$ 來指示節點 $v_{i}$ 歸於哪個簇。給定一個錨節點 $v_{i}$ 和一個節點 $v_{j}$,CDA 通過以下線性插值,在特徵級構造了一個 $v_{j}$ 的加強版本:
$\tilde{\mathbf{h}}_{j}=\alpha \mathbf{h}_{j}+(1-\alpha) \mathbf{w}_{c_{i}} \quad\quad\quad(4)$
其中,$\mathbf{w}=\left\{\mathbf{w}_{m}\right\}_{m=1}^{M}$ 表示簇原型,並在不同的批之間共享。$\tilde{\mathbf{h}}_{j}$ 包含來自 $v_{j}$ 的資訊,並且更靠近錨點節點 $v_{i}$ 所屬的集群。這些虛擬增強縮小了 SupCon 學習的特徵空間,從而遠正樣本對之間的拉強度和近負樣本對之間的推強度,以幫助保留節點的聚類分布。
本質上,$\alpha$ 控制了拉(推)原始樣本對 $\left(v_{i}, v_{j}\right)$ 的強度。我們的目標是自動調整每個樣本對的 $\alpha$ 值。這樣做的主要思想見 Figure 2。

如果錨節點 $v_{i}$ 和對比樣本 $v_{j}$ 在嵌入空間中已經保持彼此接近,我們傾向於直接進行對比。因此,我們使用一個更大的 $\alpha$ 來將來自 $v_{j}$ 的更多資訊包含到增強的樣本中。相反,如果 $v_{i}$ 和 $v_{j}$ 在嵌入空間中彼此遠離,我們使用較小的 $\alpha$ 來衰減來自 $v_{j}$ 的資訊,以保證錨點和增強樣本之間不會太遠。考慮到,$\text{Eq.3}$ 明確地模擬了每個正樣本對之間的拉力,而不是每個負樣本對之間的推,我們從正樣本對的角度設計了調整 $\alpha$ 的原則。我們將同樣的原理應用於負樣本對,實驗結果證明 CDA 有效。細化負樣本對的原理有待於在今後的工作中進行進一步的研究。在這裡,我們計算的權重 $\alpha$ 為:
${\large \alpha=\frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j}\right)}{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{h}_{j}\right)+\exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{c_{i}}\right)}} \quad\quad\quad(5)$
由於 $\mathbf{h}_{i}$ 和 $\mathbf{h}_{j}$ 位於半徑為 $1$ 的超球面的表面上,我們有 $\left\|\mathbf{h}_{i}-\mathbf{h}_{j}\right\|^{2}=2-2 \mathbf{h}_{i}^{\top} \mathbf{h}_{j}$,所以一個大的內積等價於一個小的平方歐幾里德距離。在高水平上,mixup 和CDA都採用線性插值操作來生成虛擬數據點。在這裡,我們想澄清一下CDA與混淆器之間的區別:
- mixup 通過擴大訓練集以提高神經網路的泛化能力,而CDA則旨在處理SupCon學習中的類內方差和類間相似性問題。
- 在技術上,mixup 在兩個樣本之間執行線性插值,而CDA在一個樣本和一個聚類之間執行線性插值。具體來說,我們插值一個錨的簇中心和錨的正(負)樣本的表示。
- 在學習方面,mixup 是獨立於學習過程,而 ClusterSCl 中的 CDA 被集成到學習過程中,以利用可學習的參數。
Integrating Clustering and CDA into SupCon Learning
基於CDA推導出的數據增強,我們對以下實例識別任務進行建模:
${\large \begin{aligned}p\left(s_{i} \mid v_{i}, c_{i}\right) &=\frac{\exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{s_{i}} / \tau\right)}{\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)} \\&=\frac{\exp \left(\mathbf{h}_{i}^{\top}\left(\alpha \mathbf{h}_{s_{i}}+(1-\alpha) \mathbf{w}_{c_{i}}\right) / \tau\right)}{\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top}\left(\alpha \mathbf{h}_{j}+(1-\alpha) \mathbf{w}_{c_{i}}\right) / \tau\right)}\end{aligned}} \quad\quad\quad(6)$
在執行 CDA 之前,我們需要通過以下方式知道錨定節點 $v_i$ 屬於哪個集群:
${\large p\left(c_{i} \mid v_{i}\right)=\frac{\exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{c_{i}} / \kappa\right)}{\sum\limits _{m=1}^{M} \exp \left(\mathbf{h}_{i}^{\top} \mathbf{w}_{m} / \kappa\right)}} \quad\quad\quad(7)$
其中,$\kappa$ 為用於調整預測的聚類分布的軟度的溫度參數,$p\left(c_{i} \mid v_{i}\right) $ 可以視為一個基於原型的軟聚類模組。由於我們已經對軟聚類模組 $p\left(c_{i} \mid v_{i}\right)$ 和聚類感知識別器 $p\left(s_{i} \mid v_{i}, c_{i}\right)$ 進行了建模,因此ClusterSCL 可以建模為以下實例識別任務:
$p\left(s_{i} \mid v_{i}\right)=\int p\left(c_{i} \mid v_{i}\right) p\left(s_{i} \mid v_{i}, c_{i}\right) d c_{i} \quad\quad\quad(8)$
Inference and Learning
實際上,由於對數操作內的求和,最大化整個訓練數據的對數似然值是不平凡的。我們可以採用 EM 演算法來解決這個問題,其中我們需要計算後驗分布:
${\large p\left(c_{i} \mid v_{i}, s_{i}\right)=\frac{p\left(c_{i} \mid v_{i}\right) p\left(s_{i} \mid v_{i}, c_{i}\right)}{\sum\limits _{m=1}^{M} p\left(m \mid v_{i}\right) p\left(s_{i} \mid v_{i}, m\right)} } \quad\quad\quad(9)$
然而,由於對整個節點的求和 $\sum\limits _{v_{j} \in V \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)$,計算後驗分布是禁止的。我們最大化了由以下方法給出的 $\log p\left(s_{i} \mid v_{i}\right)$ 的 evidence 下界(ELBO):
${\large \begin{array}{l}\log p\left(s_{i} \mid v_{i}\right) &\geq \mathcal{L}_{\operatorname{ELBO}}\left(\boldsymbol{\theta}, \mathbf{w} ; v_{i}, s_{i}\right)\\&\begin{aligned}:=& \mathbb{E}_{q\left(c_{i} \mid v_{i}, s_{i}\right)}\left[\log p\left(s_{i} \mid v_{i}, c_{i}\right)\right] -\operatorname{KL}\left(q\left(c_{i} \mid v_{i}, s_{i}\right) \| p\left(c_{i} \mid v_{i}\right)\right)\end{aligned}\\\end{array}} \quad\quad\quad(10)$
其中 $q\left(c_{i} \mid v_{i}, s_{i}\right)$ 是一個近似後 $p\left(c_{i} \mid v_{i}, s_{i}\right)$。ELBO的推導在附錄a中提供。在這裡,我們將變分分布形式化為:
${\large q\left(c_{i} \mid v_{i}, s_{i}\right)=\frac{p\left(c_{i} \mid v_{i}\right) \tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)}{\sum\limits _{m=1}^{M} p\left(m \mid v_{i}\right) \tilde{p}\left(s_{i} \mid v_{i}, m\right)}} \quad\quad\quad(11)$
其中 $\tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)=\exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{s_{i}} / \tau\right) / \sum_{v_{j} \in B \backslash\left\{v_{i}\right\}} \exp \left(\mathbf{h}_{i}^{\top} \tilde{\mathbf{h}}_{j} / \tau\right)$ 在一個批次 $B$ 內計算。請注意,$v_{i}$ 和 $v_{s_{i}}$ 都在該批處理中。此外,我們應用 $\tilde{p}\left(s_{i} \mid v_{i}, c_{i}\right)$ 來估計 $\text{Eq.10}$ 中的 $p\left(s_{i} \mid v_{i}, c_{i}\right)$、並在附錄B中作出說明。
我們通過一種變分EM演算法來優化模型參數,其中我們在 E 步推斷 $q\left(c_{i} \mid v_{i}, s_{i}\right)$,然後在 M 步優化ELBO。對一批節點進行取樣,我們可以最大化以下目標:
${\large \mathcal{L}_{\mathrm{ELBO}}(\boldsymbol{\theta}, \mathbf{w} ; B) \approx \frac{1}{|B|} \sum\limits _{v_{i} \in B} \frac{1}{\left|S_{i}\right|} \sum\limits _{s_{i} \in S_{i}} \mathcal{L}_{\operatorname{ELBO}}\left(\boldsymbol{\theta}, \mathbf{w} ; v_{i}, s_{i}\right) } \quad\quad\quad(12)$
我們觀察到,只有對集群原型使用隨機更新才能得到平凡的解決方案,即大多數實例被分配給同一個集群。為了緩解這一問題,我們在每個訓練階段後應用以下更新:
${\large \mathbf{w}_{m}=\frac{1}{\left|\bar{V}_{m}\right|} \sum\limits_{v_{i} \in \bar{V}_{m}} \mathbf{h}_{i}, m=1,2, \cdots, M } \quad\quad\quad(13)$
其中,$\bar{V}_{m}$ 表示由 METIS 導出的第 $m$ 個圖社區中的節點集。在訓練之前,我們根據節點間的互連將整個圖 $G$ 劃分為 $M$ 個圖社區。我們使用社區來粗略地描述集群,並對每個社區中的節點嵌入進行平均,以在每個訓練階段後更新集群原型。請注意,ClusterSCL 採用了 $Eq. 7$,為每個節點推導出一個細化的軟集群分布。METIS 輸出的硬集群分布僅用於原型更新。此外,我們觀察到需要對 $\kappa$ 進行細粒度搜索,這是低效的。根據經驗,我們使用一個小的 $\kappa$ 來推導一個相對可靠的聚類預測,並引入一個熵項來平滑預測的聚類分布。通過這樣做,我們可以避免在 $\kappa$ 上的細粒度搜索。最後,將 ClusterSCL 損失函數形式化為:
${\large \mathcal{L}(\boldsymbol{\theta}, \mathbf{w} ; B)=-\mathcal{L}_{\mathrm{ELBO}}(\boldsymbol{\theta}, \mathbf{w} ; B)+\frac{\eta}{|B|} \sum\limits _{v_{i} \in B} \sum\limits _{c_{i}=1}^{M} p\left(c_{i} \mid v_{i}\right) \log p\left(c_{i} \mid v_{i}\right)} \quad\quad\quad(14)$
其中,$\eta \in(0,1]$ 為控制平滑強度的熵項的權值。
Algorithm 1 顯示了使用Clusterscl進行訓練的偽程式碼。我們在附錄C中提供了 ClusterSCL 的複雜性分析。

3 Experiments
實驗通過回答以下研究問題來展開:(1)ClusterSCL 如何在節點分類任務上執行?(2)CDA是否生效?(3)ClusterSCL 在不同大小的標記訓練數據下表現如何?
節點分類
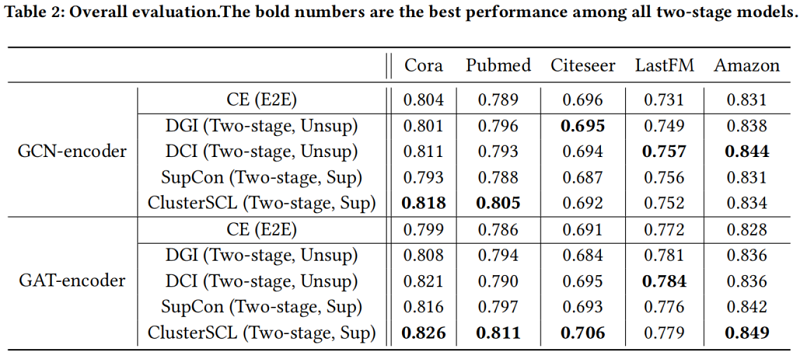
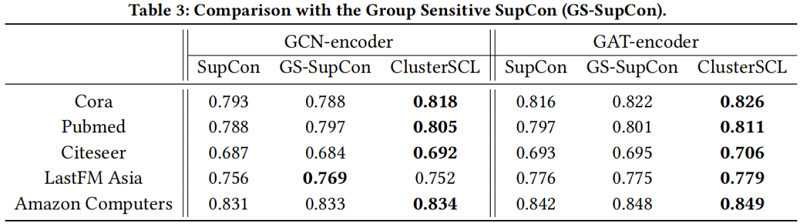
CDA 有效性驗證
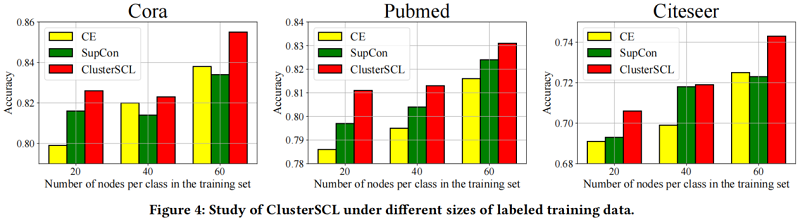
在不同大小的標記訓練數據下的 ClusterSCL 的研究
4 Conclusion
這項工作初步研究了用於節點分類的圖神經網路的監督學習。我們提出了一種簡單而有效的對比學習方案,稱為聚類感知監督對比學習(聚類scl)。ClusterSCL改進了監督對比(SupCon)學習,並強調了在SupCon學習過程中保留內在圖屬性的有效性,從而減少了由類內方差和類間相似性引起的負面影響。ClusterSCL比流行的交叉熵、SupCon和其他圖對比損失更具有優勢。我們認為,ClusterSCL的思想並不局限於圖上的節點分類,並可以啟發表示學習的研究。


