(Bezier)貝塞爾曲在路徑規劃的運用
前言
之前被安排了活,一個局部區域機器運動控制的工作,大致是一個機器位於一個極限區域時候,機器要進入一個特殊的機制,使得機器可以安全的走出來。其中用到了bezier曲線進行優化路徑,今天寫一下,正好也給大家分享一下工作和實踐的情況。
作者:良知猶存
轉載授權以及圍觀:歡迎關注微信公眾號:羽林君
或者添加作者個人微信:become_me
貝塞爾曲線基本介紹
線段都可以被拆分成兩個坐標的差來表示,如下面一階的貝塞爾曲線,P0到P1,可以用一個t進行拆分這段線,分別是線段 t(P0~P1)、線段 1-t(P0~P1),P0和P1叫做, 這條條貝塞爾的兩個控制點,而貝塞爾曲線至少要有兩個控制點(就是下面的這條直線,一階貝塞爾曲線)。在貝塞爾曲線與控制點位置相關,這意味著在曲線生成過程中,我們可以通過調節控制點的位置,進而調整整個曲線。
貝塞爾的階數和次數是一樣的,二階貝塞爾,三個點,最高次數二次。例:二階貝塞爾:三個點,兩個線段,以所有等比的點組合成的曲線叫做二階貝塞爾曲線。
接下來給大家介紹一下貝塞爾曲線的推導工程,也比較簡單,並且網上的介紹也挺多的:
一階:
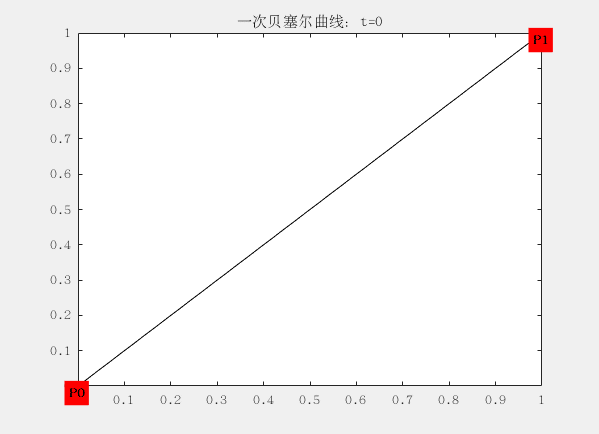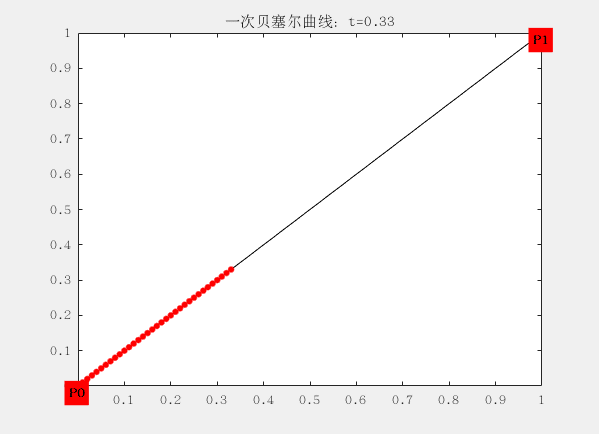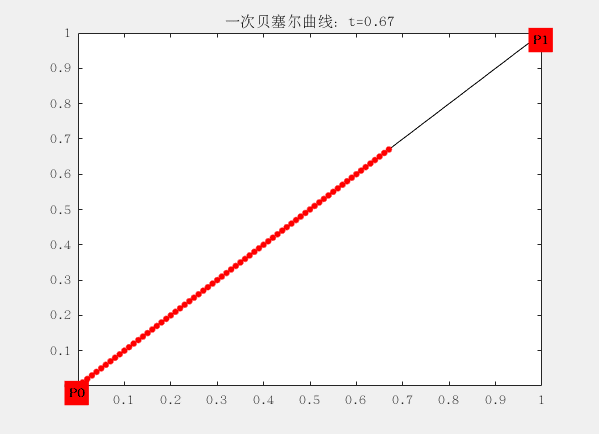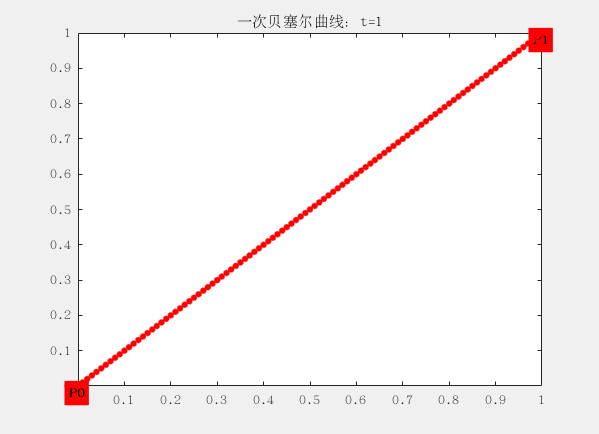
這裡面有兩個控制點為$ P_0 (0,0) 和P_1 (1,1)$ ,對應的曲線方程為:
$$ B\big( t \big) = P_t = (1 – t) P_0 + tP_1 = P_0 + (P_1 – P_0)t $$
tϵ[0,1]
這個方程可以理解為,從$P_0$出發,朝著$P_1$的方向前進$||P_1-P_0||t$的距離,從而得到了點B(t)的位置。t從0逐漸遞增到1,這個過程完成,就成了我們所看到的曲線。
另外,之所以是一階貝塞爾曲線是因為方程是關於t的一階多項式,多階也是一樣。
二階:
有三個控制點,這裡的 P0、P1、P2 分別稱之為控制點,曲線的產生完全與這三個點位置相關。
與一階有些區別就在於三個控制點形成兩個線段,每個線段上有一個點在運動,於是得到兩個點;
再使用兩個點形成一個線段,這個線段上有一個點在運動,於是得到一個點;最後一個點的運動軌跡便構成了二階貝塞爾曲線。
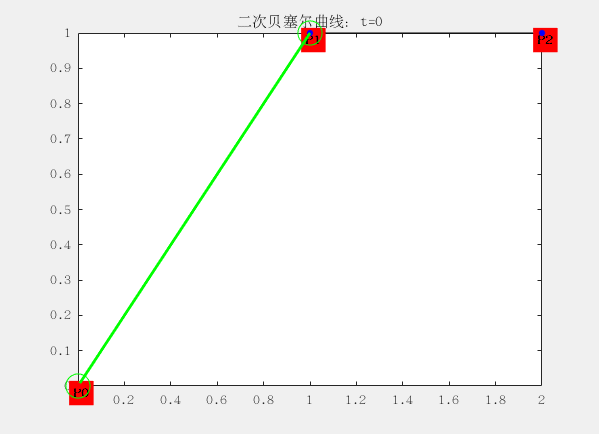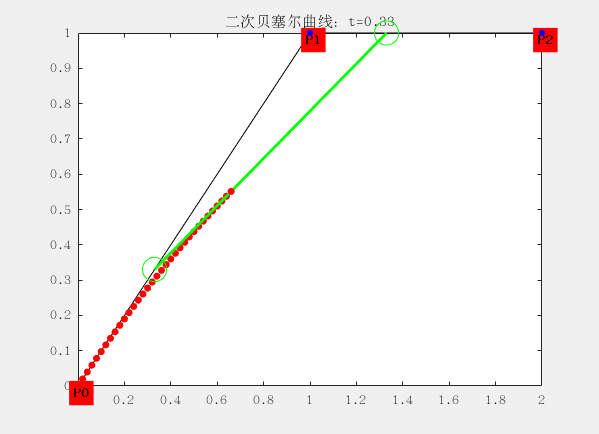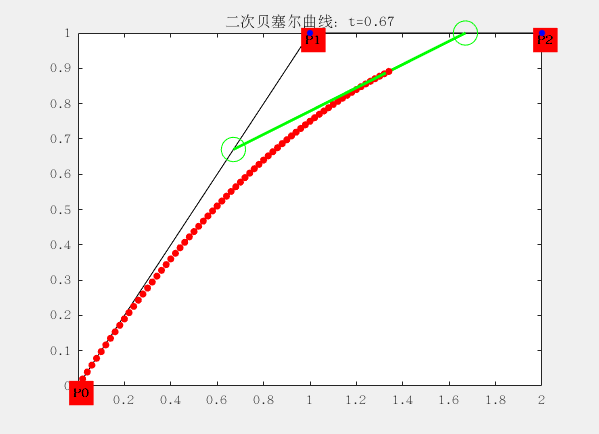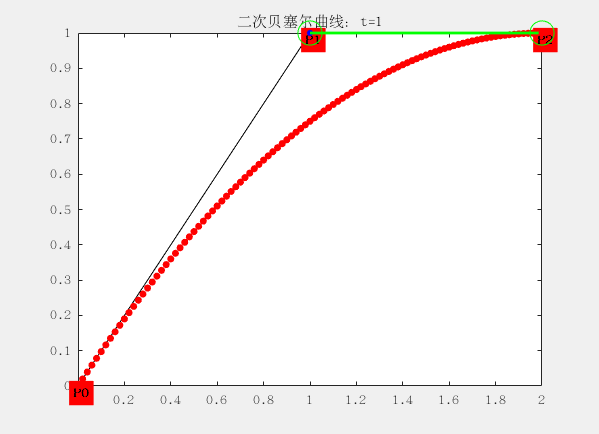
對應的曲線方程為:
$$ P_a = (1 – t) P_0 + tP_1 = P_0 + (P_1 – P_0)t $$
$$ P_b = (1 – t) P_1 + tP_2 = P_1 + (P_2 – P_1)t $$
$$ P_t = (1 – t) P_a + tP_b = P_a + (P_b – P_a)t $$
這是一條迭代公式,每次迭代都會少掉一個「點」。
最後得:
$$ B\big( t \big) = P_t = (1 – t)^2 P_0 + 2t(t -1)P_1 + t^2 P_2 $$
三階:
有四個控制點
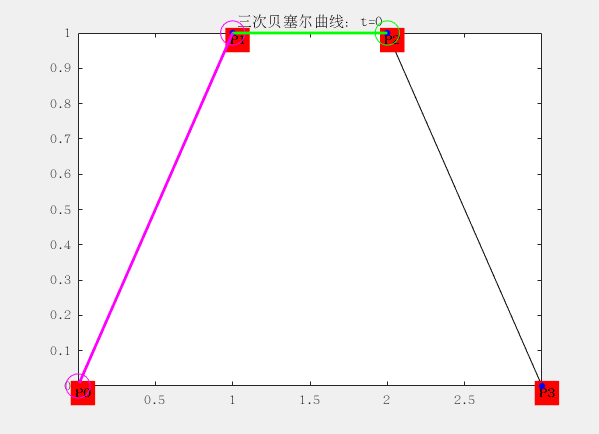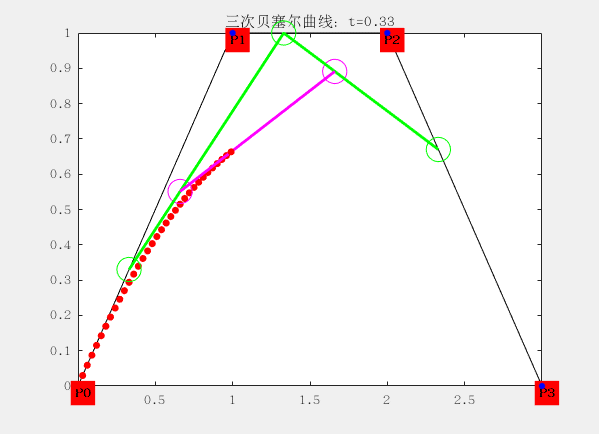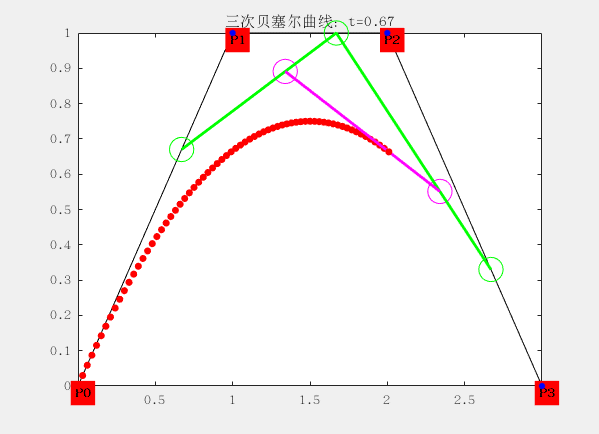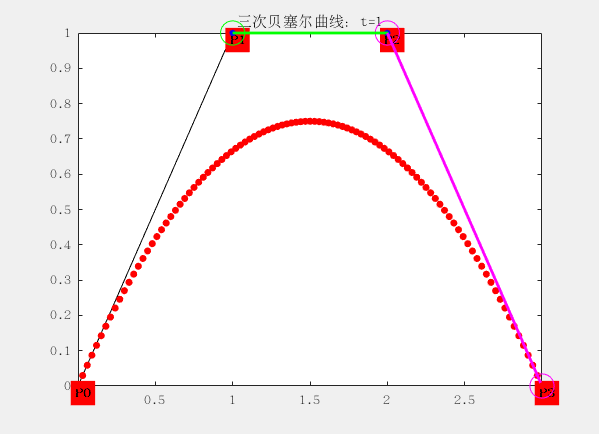
設控制點為P0,P1,P2和P4,曲線方程為:
$$ B\big( t \big) = P_t = (1 – t)^3 P_0 + 3t(t -1)^2t P_1 + 3t^2(1-t) P_2+t^3P_3 $$
配圖這是matlab生成的gif動畫,大家想要的也可以找我,程式碼私發給大家。
N階:
我們發現,實際上是每輪都是 n 個點,形成 n-1 條線段,每個線段上有一個點在運動,那麼就只關注這 n-1 個點,循環往複。最終只剩一個點時,它的軌跡便是結果。
如此一來,你會發現貝塞爾曲線內的遞歸結構。實際上,上述介紹的分別是一階、二階、三階的貝塞爾曲線,貝塞爾曲線可以由階數遞歸定義。
N階貝塞爾曲線公式:
$$ B\big( t \big) = \sum\limits_{i=0}^{n} \big(_{i}^{n} \big) P_i(1-t)^{n-i} t^i ,t\in [0,1]$$
貝塞爾曲線應用
貝塞爾曲線在動畫中有應用,前端以及一些其他顯示要求;此外在路徑規划過程中,也會使用貝塞爾曲線進行規劃好路徑再優化,我就是使用了後者進行優化規劃好的路徑,使得機器行走更加順暢,不過使用中大家需要按照機器實際相應來進行調整t的精度以及階數。
由於貝塞爾曲線本身的數學表達式便是一條遞歸式,所以決定採用遞歸的方式來實現。程式碼如下,BezierCurve函數實現貝塞爾曲線迭代,UseBezierOptimizePath函數的第二個參數進行控制使用的階數,最後調用opencv實現可視化效果。
#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <vector>
using namespace cv;
using std::cout;
using std::endl;
using std::vector;
template <typename T>
T BezierCurve(T src)
{
if (src.size() < 1)
return src;
const float step = 0.003;//1.0/step
T res;
if (src.size() == 1) {//遞歸結束條件
for (float t = 0; t < 1; t += step)
res.push_back(src[0]);
return res;
}
T first_part{};
T second_part{};
first_part.assign(src.begin(), src.end() - 1);
second_part.assign(src.begin() + 1, src.end());
T pln1 = BezierCurve(first_part);
T pln2 = BezierCurve(second_part);
for (float t = 0; t < 1; t += step)
{
typename T::iterator::value_type temp{};
temp += pln1[cvRound(1.0 / step * t)] * (1.0 - t) ;
temp += pln2[cvRound(1.0 / step * t)] * t;
res.emplace_back(temp);
}
return res;
}
template <typename T>
T UseBezierOptimizePath(T path,uint8_t order_number)
{
if(path.size() < order_number)
return {};
T new_path{};
for(uint8_t i=0;i<path.size()-(order_number-1);i+=(order_number-1))
{
T tmp = BezierCurve(T(&path[i],&path[ i + order_number]));
new_path.insert(new_path.begin(),tmp.begin(),tmp.end());
}
return new_path;
}
int main(int argc, char const* argv[])
{
while (1) {
cout<< endl;
cout<< endl;
cout<< endl;
vector<Point2f> path;
RNG rng;
for (int i = 1; i <8; i++)
path.push_back(Point2f(i * 800 / 8, random() % 800));//rng.uniform(0,800)));//cvRandInt(rng) % 800));
Mat img(900, 1200, CV_8UC3);
img = 0;
for(uint8_t i =0;i < path.size() -1;i++)
{
cout<< path[i]<< ","<< endl;
line(img,Point(path[i].x, path[i].y),Point(path[i+1].x, path[i+1].y), Scalar(255, 0, 0), 16, LINE_AA, 0);
}
cout<< endl;
// imshow("line", img);
for (int i = 0; i < path.size(); i++)
circle(img, path[i], 3, Scalar(0, 0, 255), 10); //BGR
// vector<Point2f> bezierPath = bezierCurve(path);
vector<Point2f> bezierPath = UseBezierOptimizePath(path,4);
for (int i = 0; i < bezierPath.size(); i++) {
// circle(img, bezierPath[i], 3, Scalar(0, 255, 255), 3); //BGR
img.at<cv::Vec3b>(cvRound(bezierPath[i].y), cvRound(bezierPath[i].x)) = { 0, 255, 255 };
// printf("pose(%f %f)\n",bezierPath[i].x,bezierPath[i].y);
imshow("black", img);
// waitKey(10);
}
if (waitKey(0) == 'q')
break;
}
return 0;
}
顯示效果如下:
三階
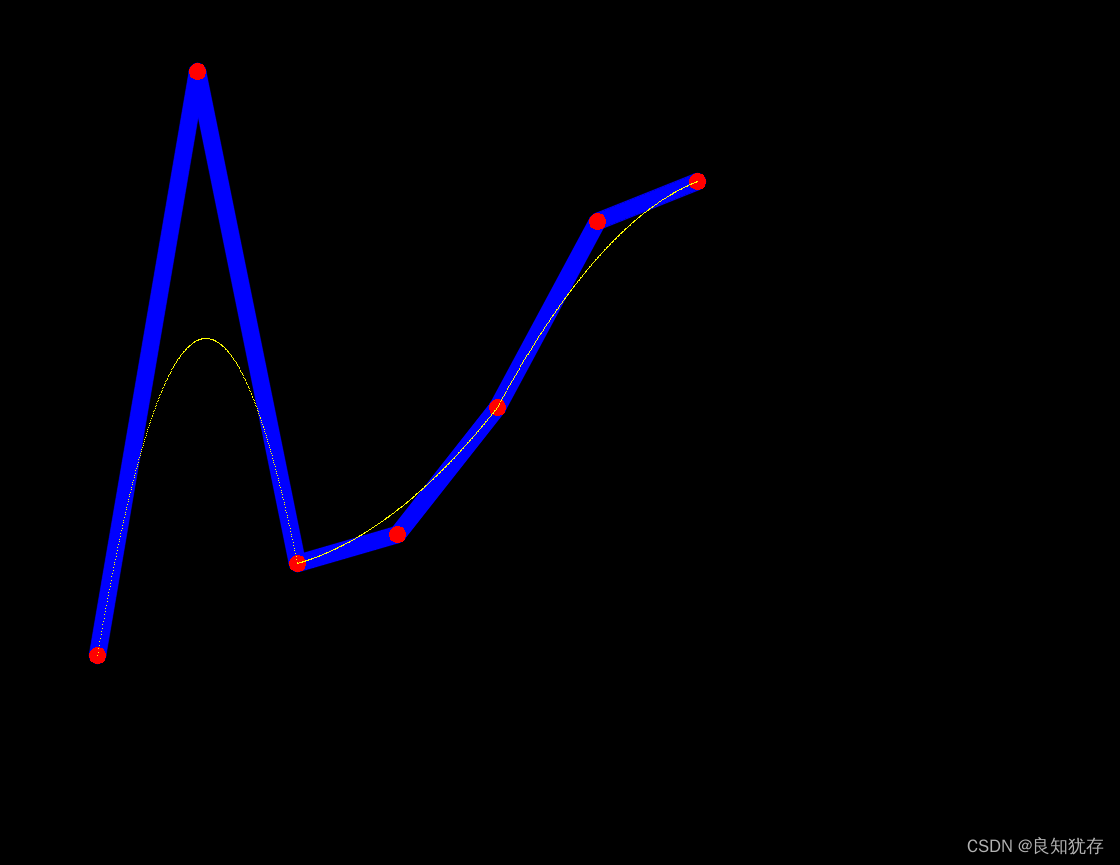
四階
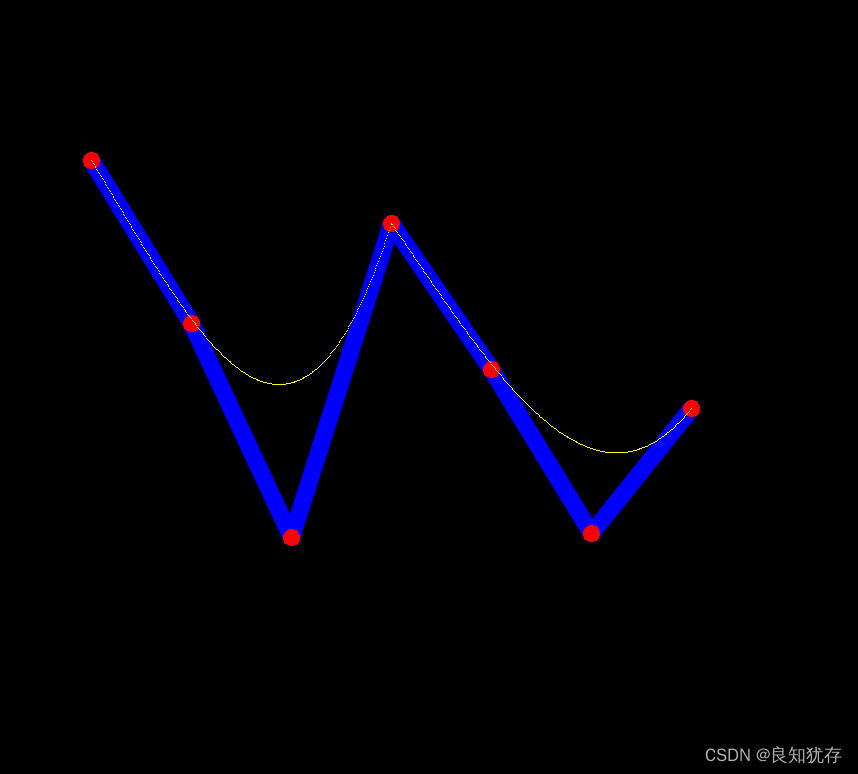
結語
這就是我自己的一些設不貝塞爾曲線的使用分享。如果大家有更好的想法和需求,也歡迎大家加我好友交流分享哈。
作者:良知猶存,白天努力工作,晚上原創公號號主。公眾號內容除了技術還有些人生感悟,一個認真輸出內容的職場老司機,也是一個技術之外豐富生活的人,攝影、音樂 and 籃球。關注我,與我一起同行。
‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧ END ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧
推薦閱讀
【3】CPU中的程式是怎麼運行起來的 必讀
本公眾號全部原創乾貨已整理成一個目錄,回復[ 資源 ]即可獲得。


