論文解讀(SAGPool)《Self-Attention Graph Pooling》
論文資訊
論文標題:Self-Attention Graph Pooling
論文作者:Junhyun Lee, Inyeop Lee, Jaewoo Kang
論文來源:2019, ICML
論文地址:download
論文程式碼:download
1 Introduction
圖池化三種類型:
-
- Topology based pooling;
- Hierarchical pooling;(使用所有從 GNN 獲得的節點表示)
- Hierarchical pooling;
關於 Hierarchical pooling 聚類分配矩陣:
$\begin{array}{j}S^{(l)}=\operatorname{softmax}\left(\mathrm{GNN}_{l}\left(A^{(l)}, X^{(l)}\right)\right) \\A^{(l+1)}=S^{(l) \top} A^{(l)} S^{(l)}\end{array} \quad\quad\quad\quad(1)$
gPool 取得了與 DiffPool 相當的性能,gPool 需要的存儲複雜度為 $\mathcal{O}(|V|+|E|)$,而 DiffPool 需要 $\mathcal{O}\left(k|V|^{2}\right)$,其中 $V$、$E$ 和 $k$ 分別表示頂點、邊和池化率。gPool 使用一個可學習的向量 $p$ 來計算投影分數,然後使用這些分數來選擇排名靠前的節點。投影得分由 $p$ 與所有節點的特徵之間的點積得到。這些分數表示可以保留的節點的資訊量。下面的公式大致描述了 gPool 中的池化過程:
$\begin{array}{l} y=X^{(l)} \mathbf{p}^{(l)} /\left\|\mathbf{p}^{(l)}\right\|\\ \mathrm{idx}=\operatorname{top}-\operatorname{rank}(y,\lceil k N\rceil)\\A^{(l+1)}=A_{\mathrm{idx}, \mathrm{idx}}^{(l)}\end{array} \quad\quad\quad\quad(2)$
2 Method
框架如下:
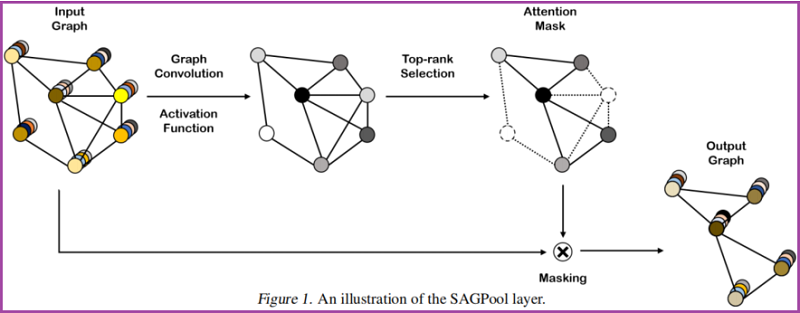
2.1. Self-Attention Graph Pooling
Self-attention mask
本文使用圖卷積來獲得自注意分數:
$Z=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} X \Theta_{a t t}\right) \quad\quad\quad\quad(3)$
其中,自注意得分 $Z \in \mathbb{R}^{N \times 1}$、鄰接矩陣 $\tilde{A} \in \mathbb{R}^{N \times N}$、注意力參數矩陣 $\Theta_{a t t} \in \mathbb{R}^{F \times 1}$、特徵矩陣 $X \in \mathbb{R}^{N \times F}$、度矩陣 $\tilde{D} \in \mathbb{R}^{N \times N}$。
這裡考慮節點選擇方法,即使輸入不同大小和結構的圖,也會保留輸入圖的部分節點。
$\begin{array}{l} \mathrm{idx}=\operatorname{top}-\operatorname{rank}(Z,\lceil k N\rceil)\\Z_{\text {mask }}=Z_{\mathrm{idx}}\end{array} \quad\quad\quad\quad(4)$
基於自注意得分 $Z$ ,選擇保留前 $ \lceil k N\rceil$ 個節點,其中 $k \in(0,1]$ 代表著池化率(pooling ratio),$Z_{\text{mask}}$ 是 feature attention mask。。
Graph pooling
接著獲得新特徵矩陣和鄰接矩陣:
$\begin{array}{l} X^{\prime}=X_{\mathrm{idx},:}\\X_{\text {out }}=X^{\prime} \odot Z_{\text {mask }}\\A_{\text {out }}=A_{\mathrm{idx}, \mathrm{idx}}\end{array} \quad\quad\quad\quad(5)$
其中,$\odot$ is the broadcasted elementwise product。
Variation of SAGPool
$Z=\sigma(\operatorname{GNN}(X, A)) \quad\quad\quad\quad(6)$
$Z=\sigma\left(\operatorname{GNN}\left(X, A+A^{2}\right)\right) \quad\quad\quad\quad(7)$
$Z=\sigma\left(\mathrm{GNN}_{2}\left(\sigma\left(\mathrm{GNN}_{1}(X, A)\right), A\right)\right) \quad\quad\quad\quad(8)$
$Z=\frac{1}{M} \sum_{m} \sigma\left(\mathrm{GNN}_{m}(X, A)\right) \quad\quad\quad\quad(9)$
2.2 Model Architecture
本節用來驗證模組的有效性。
Convolution layer
圖卷積 GCN:
$h^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} h^{(l)} \Theta\right) \quad\quad\quad\quad(10)$
與 $\text{Eq.3}$ 不同的是,$\Theta \in \mathbb{R}^{F \times F^{\prime}}$ 。
Readout layer
根據 JK-net architecture 的思想:
$s=\frac{1}{N} \sum_{i=1}^{N} x_{i} \| \max _{i=1}^{N} x_{i} \quad\quad\quad\quad(11)$
其中:
-
- $N$ 代表著節點的個數;
- $x_{i}$ 代表著第 $i$ 個節點的特徵向量;
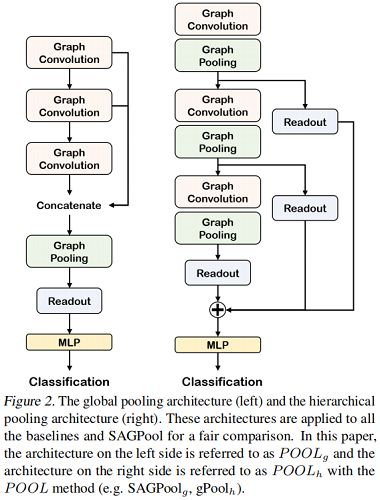
Global pooling architecture & Hierarchical pooling architecture
對比如下:
3 Experiments
數據集

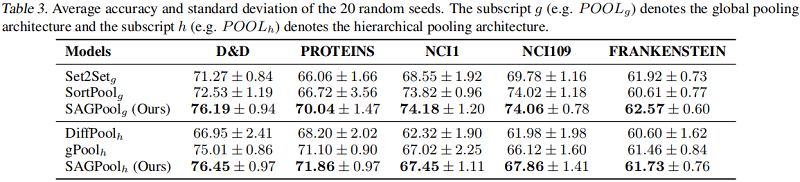
基準線實驗
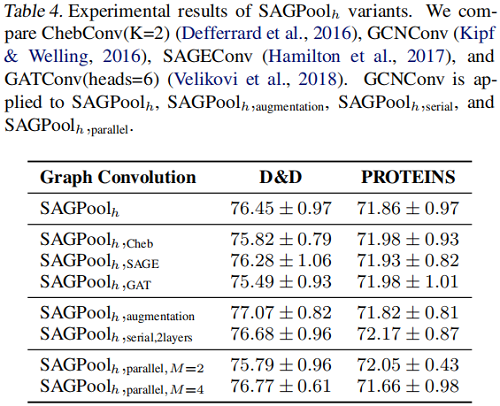
SAGPool 的變體
4 Conclusion
本文提出了一種基於自注意的SAGPool圖池化方法。我們的方法具有以下特徵:分層池、同時考慮節點特徵和圖拓撲、合理的複雜度和端到端表示學習。SAGPool使用一致數量的參數,而不管輸入圖的大小如何。我們工作的擴展可能包括使用可學習的池化比率來獲得每個圖的最優聚類大小,並研究每個池化層中多個注意掩模的影響,其中最終的表示可以通過聚合不同的層次表示來獲得。


