斯坦福NLP課程 | 第1講 – NLP介紹與詞向量初步

作者：韓信子@ShowMeAI，路遙@ShowMeAI，奇異果@ShowMeAI
教程地址：//www.showmeai.tech/tutorials/36
本文地址：//www.showmeai.tech/article-detail/231
聲明：版權所有，轉載請聯繫平台與作者並註明出處

收藏ShowMeAI查看更多精彩內容

NLP介紹與詞向量初步
ShowMeAI為斯坦福CS224n《自然語言處理與深度學習(Natural Language Processing with Deep Learning)》課程的全部課件，做了中文翻譯和注釋，並製作成了GIF動圖！

詞向量、SVD分解與Word2vec
本講內容的深度總結教程可以在這裡 查看。影片和課件等資料的獲取方式見文末。

引言

CS224n是頂級院校斯坦福出品的深度學習與自然語言處理方向專業課程。核心內容覆蓋RNN、LSTM、CNN、transformer、bert、問答、摘要、文本生成、語言模型、閱讀理解等前沿內容。

ShowMeAI將從本節開始，依託cs224n課程為主框架，逐篇為大家梳理NLP的核心重點知識原理。

NLP介紹與詞向量初步

本篇內容覆蓋：

第1課直接切入語言和詞向量，講解了自然語言處理的基本概念，文本表徵的方法和演進，包括word2vec等核心方法，詞向量的應用等。

  • 自然語言與文字
  • word2vec介紹
  • word2vec目標函數與梯度
  • 演算法優化基礎
  • word2vec構建的詞向量模式

Introduction and Word Vectors

1. 自然語言與辭彙含義

1.1 人類的語言與辭彙含義

咱們先來看看人類的高級語言。

人類的語言與辭彙含義

人類之所以比類人猿更「聰明」，是因為我們有語言，因此是一個人機網路，其中人類語言作為網路語言。人類語言具有資訊功能和社會功能。

據估計，人類語言只有大約5000年的短暫歷史。語言和寫作是讓人類變得強大的原因之一。它使知識能夠在空間上傳送到世界各地，並在時間上傳送。

但是，相較於如今的互聯網的傳播速度而言，人類語言是一種緩慢的語言。然而，只需人類語言形式的幾百位資訊，就可以構建整個視覺場景。這就是自然語言如此迷人的原因。

1.2 我們如何表達一個詞的意思？

我們如何表達一個詞的意思？

我們如何表達一個詞的含義呢？有如下一些方式：

  • 用一個詞、片語等表示的概念。
  • 一個人想用語言、符號等來表達的想法。
  • 表達在作品、藝術等方面的思想。

理解意義的最普遍的語言方式(linguistic way)：語言符號與語言意義（想法、事情）的相互對應

  • denotational semantics：語義
\[signifier(symbol) \Leftrightarrow signified(idea \quad or \quad thing)
\]

1.3 如何在電腦里表達詞的意義

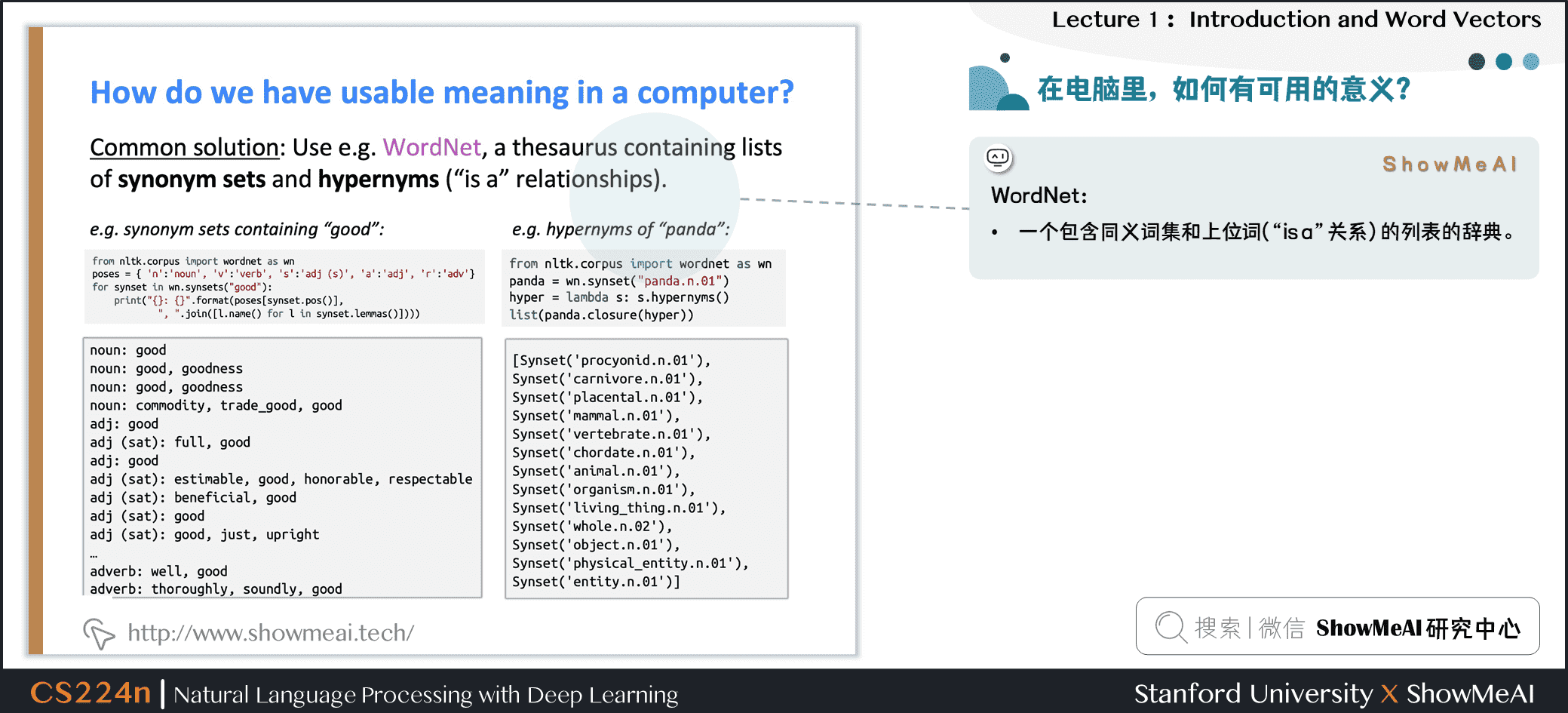
要使用電腦處理文本辭彙，一種處理方式是WordNet：即構建一個包含同義詞集和上位詞(「is a」關係)的列表的辭典。

英文當中確實有這樣一個wordnet，我們在安裝完NLTK工具庫和下載數據包後可以使用，對應的python程式碼如下：

from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
        print("{}: {}".format(poses[synset.pos()], ", ".join([l.name() for l in synset.lemmas()])))

from nltk.corpus import wordnet as wn
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))

結果如下圖所示：
如何在電腦里表達詞的意義

1.4 WordNet的問題

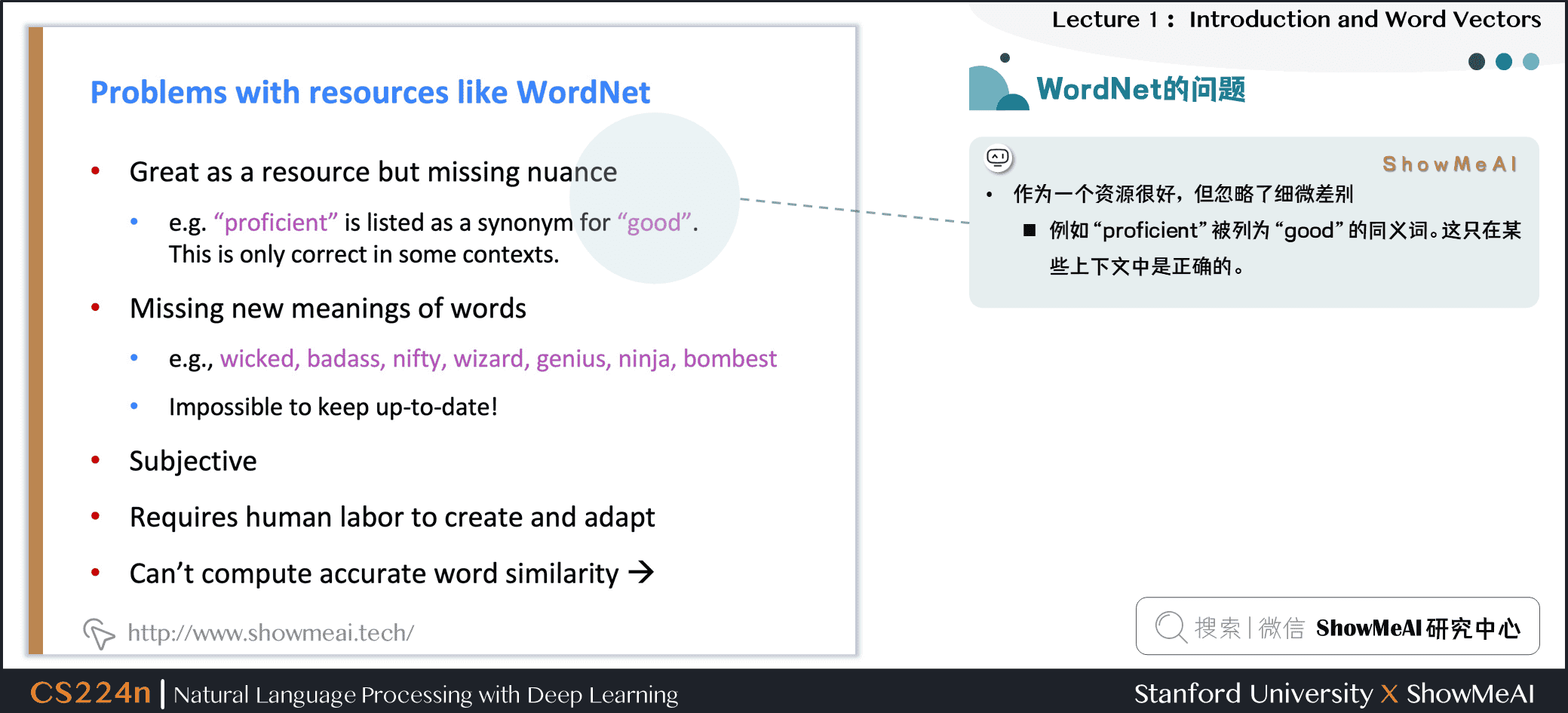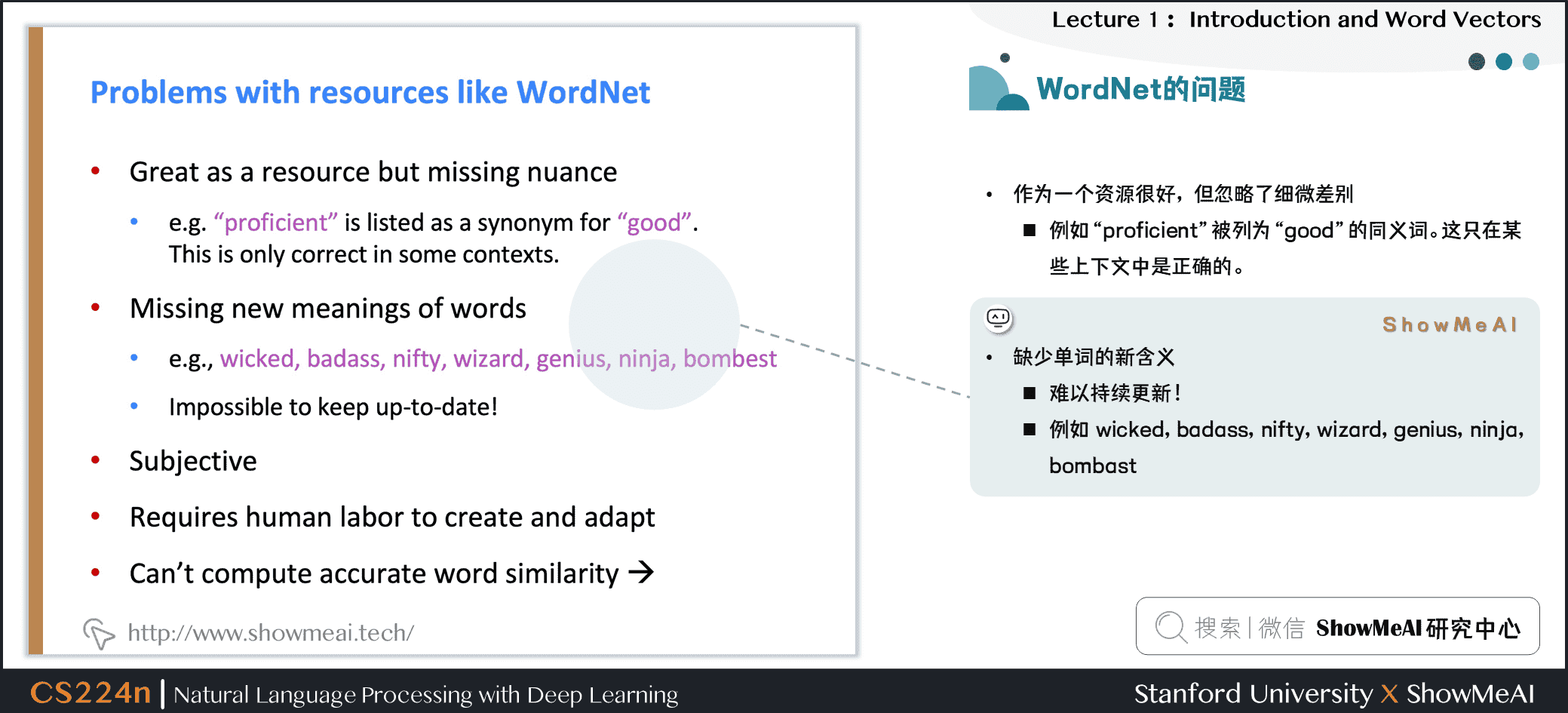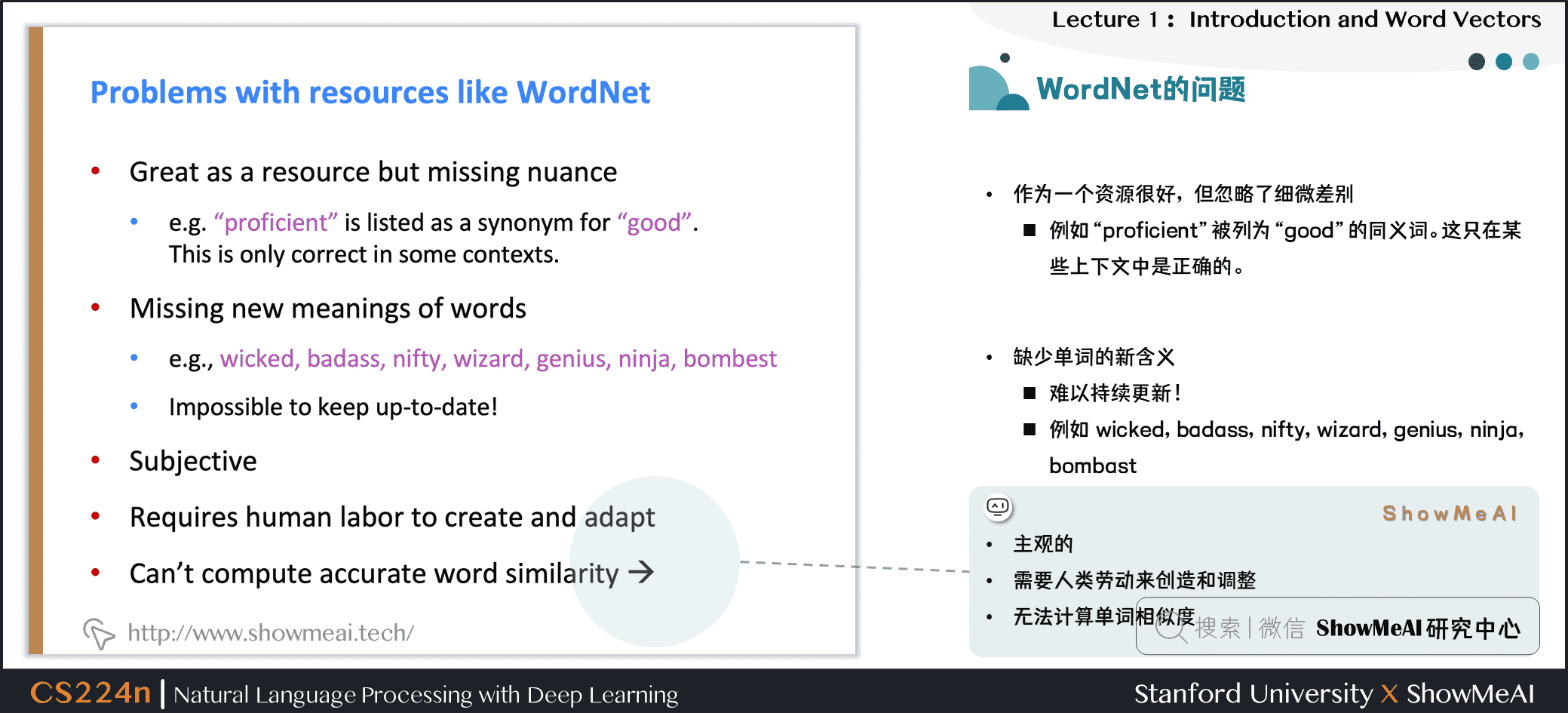
WordNet的問題

WordNet大家可以視作1個專家經驗總結出來的辭彙表，但它存在一些問題：

① 忽略了辭彙的細微差別

  • 例如「proficient」被列為「good」的同義詞。這隻在某些上下文中是正確的。

② 缺少單詞的新含義

  • 難以持續更新！
  • 例如：wicked、badass、nifty、wizard、genius、ninja、bombast

③ 因為是小部分專家構建的，有一定的主觀性

④ 構建與調整都需要很多的人力成本

⑤ 無法定量計算出單詞相似度

1.5 文本(辭彙)的離散表徵

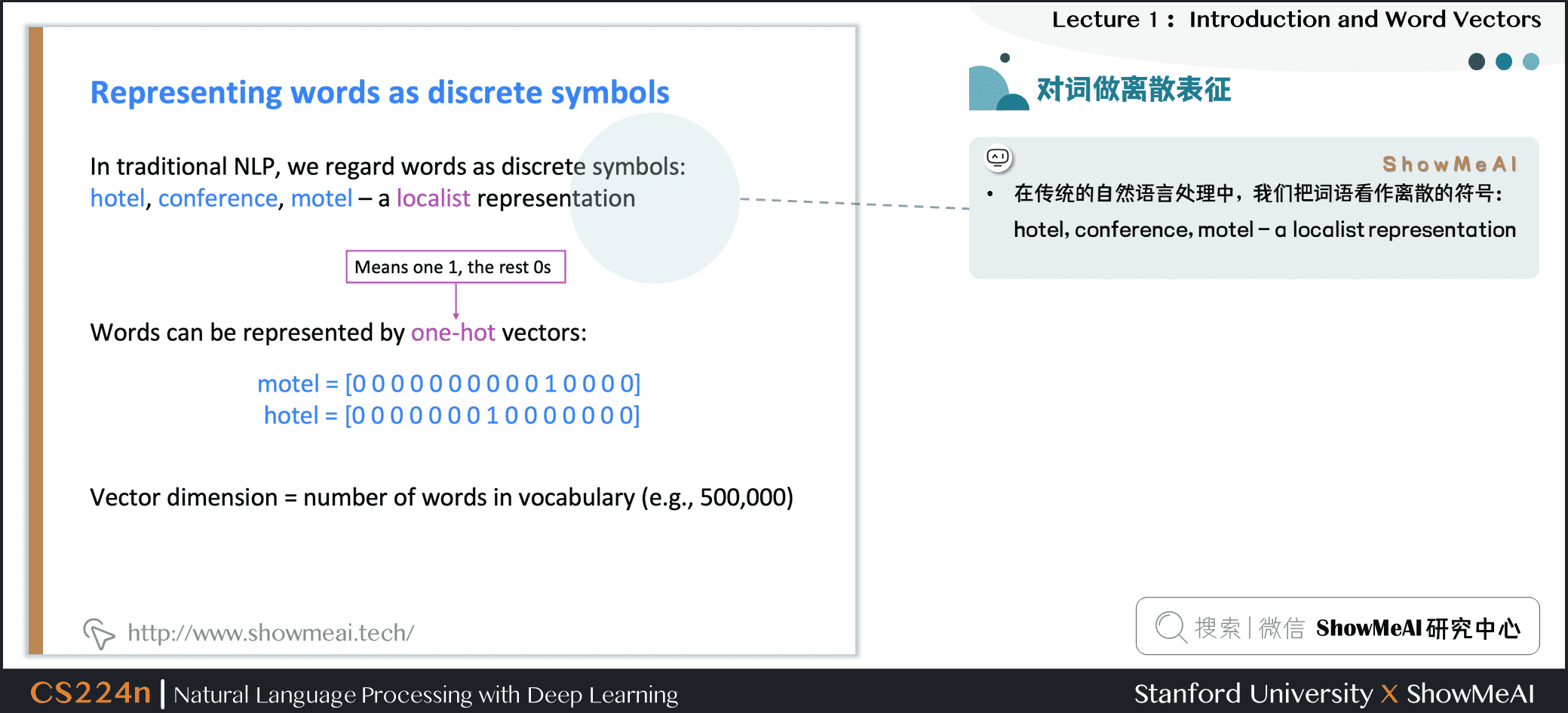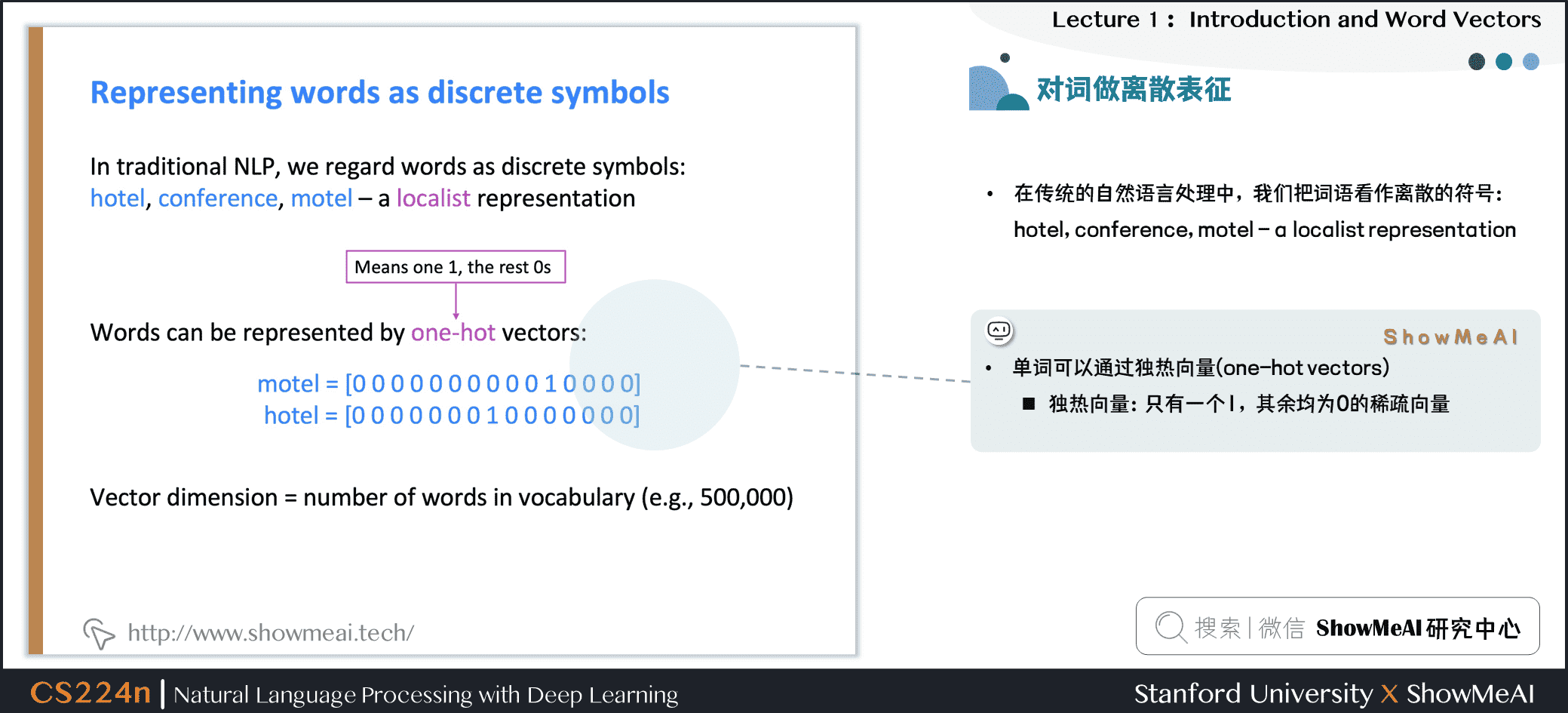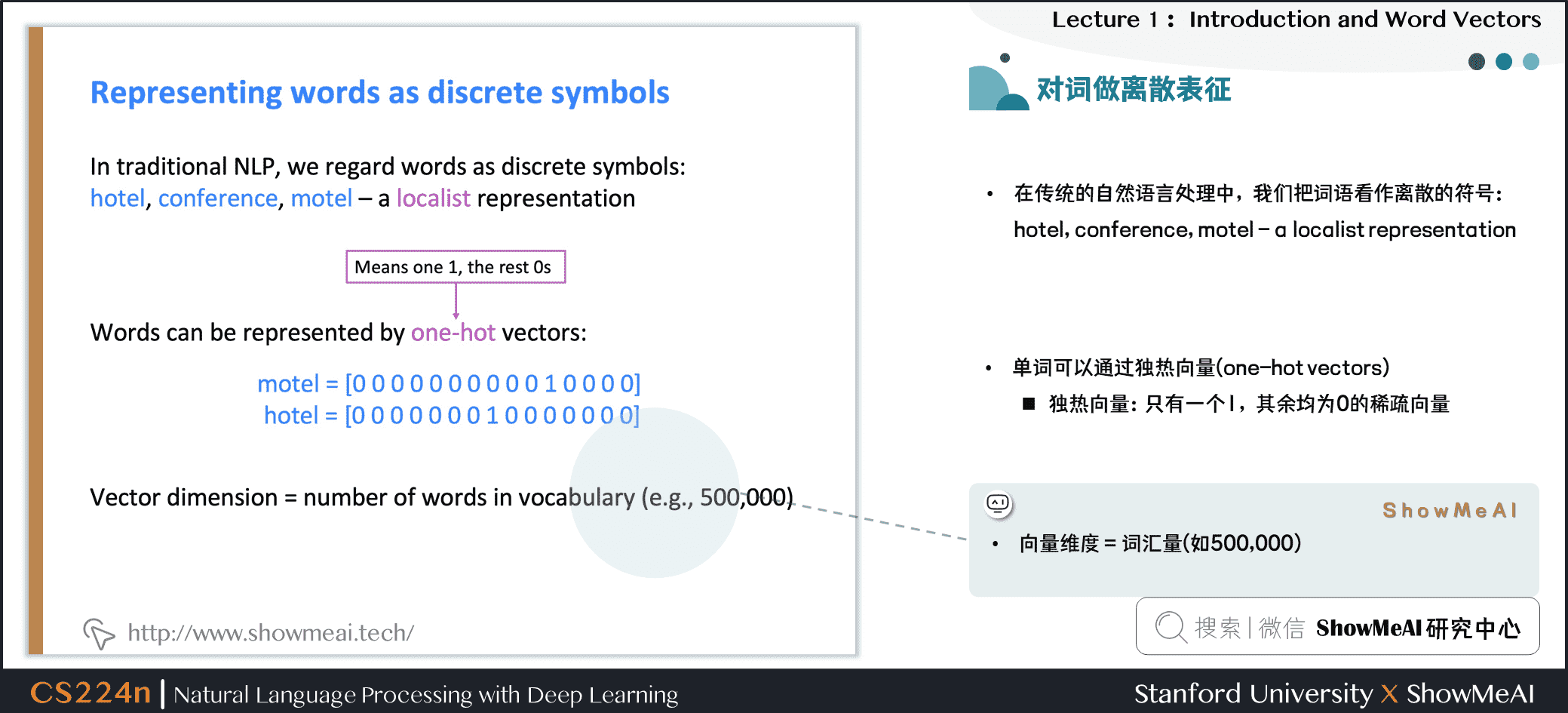
文本(辭彙)的離散表徵

在傳統的自然語言處理中，我們會對文本做離散表徵，把詞語看作離散的符號：例如hotel、conference、motel等。

一種文本的離散表示形式是把單詞表徵為獨熱向量(one-hot vectors)的形式

  • 獨熱向量：只有一個1，其餘均為0的稀疏向量

在獨熱向量表示中，向量維度=辭彙量(如500,000)，以下為一些獨熱向量編碼過後的單詞向量示例：

\[motel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0]
\]

\[hotel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]
\]

1.6 離散表徵的問題

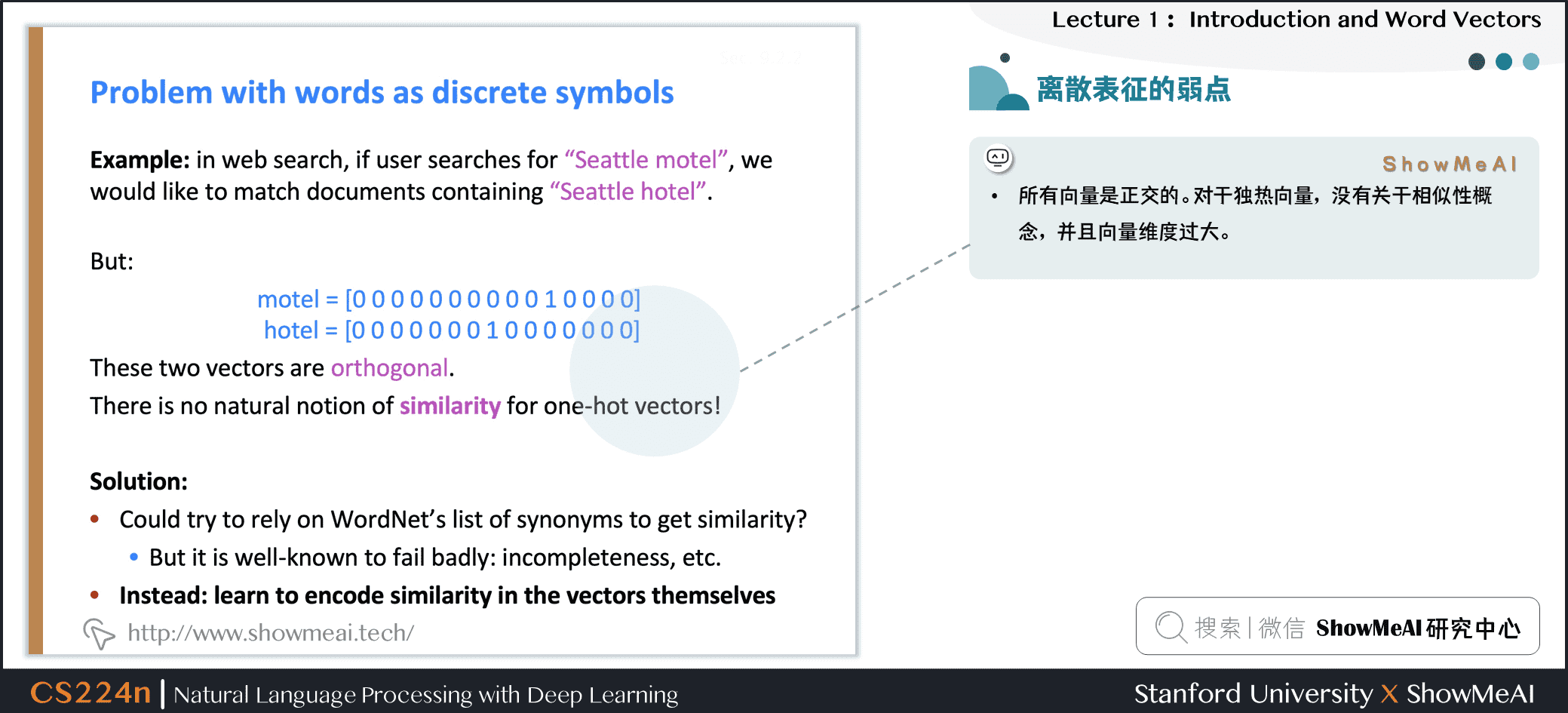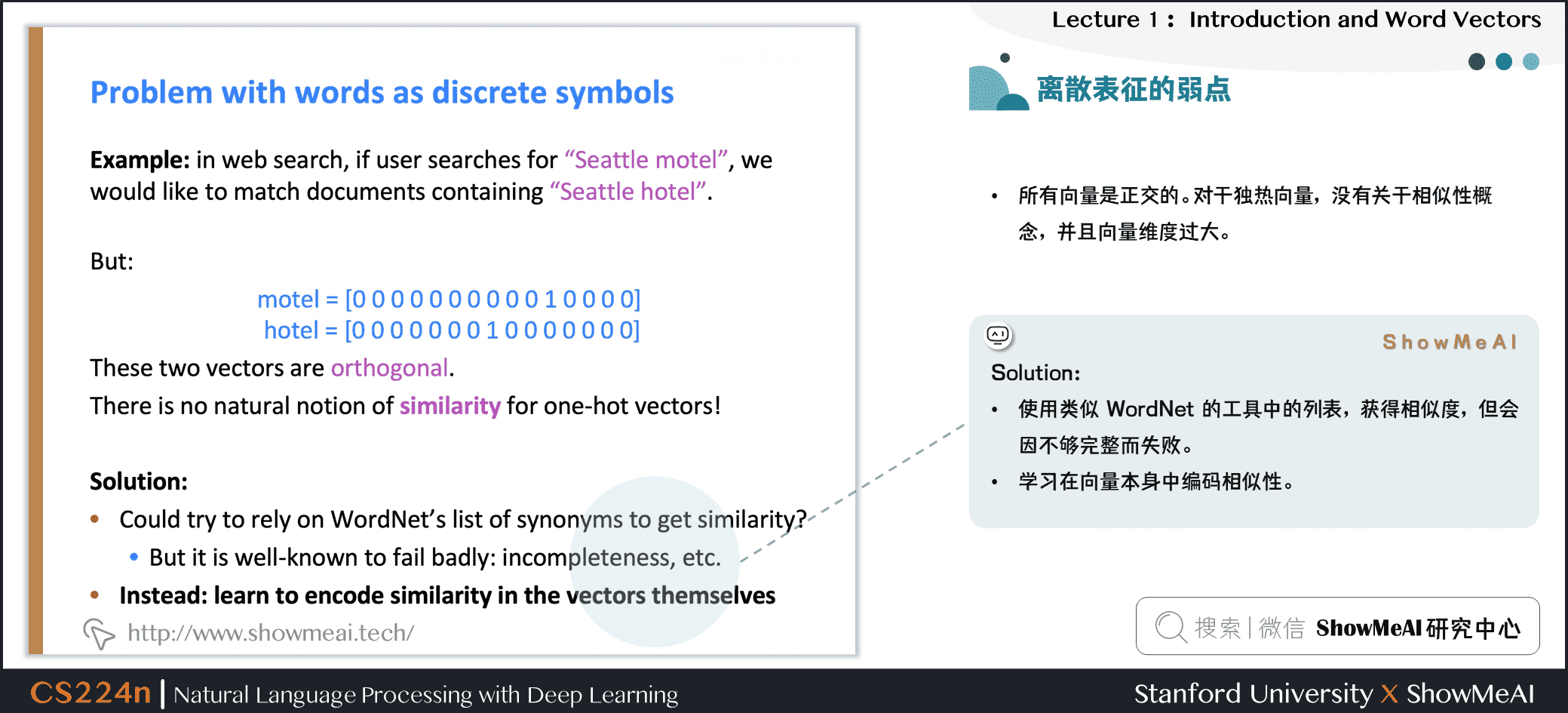
離散表徵的問題

在上述的獨熱向量離散表徵里，所有詞向量是正交的，這是一個很大的問題。對於獨熱向量，沒有關於相似性概念，並且向量維度過大。

對於上述問題有一些解決思路：

  • ① 使用類似WordNet的工具中的列表，獲得相似度，但會因不夠完整而失敗
  • ② 通過大量數據學習詞向量本身相似性，獲得更精確的稠密詞向量編碼

1.7 基於上下文的辭彙表徵

近年來在深度學習中比較有效的方式是基於上下文的辭彙表徵。它的核心想法是：一個單詞的意思是由經常出現在它附近的單詞給出的 「You shall know a word by the company it keeps」 (J. R. Firth 1957: 11)。

基於上下文的辭彙表徵

這是現代統計NLP最成功的理念之一，總體思路有點物以類聚，人以群分的感覺。

  • 當一個單詞 \(w\)出現在文本中時，它的上下文是出現在其附近的一組單詞(在一個固定大小的窗口中)
  • 基於海量數據，使用 \(w\)的許多上下文來構建 \(w\)的表示

如圖所示，banking的含義可以根據上下文的內容表徵。

2.Word2vec介紹

2.1 詞向量表示

下面我們要介紹詞向量的構建方法與思想，我們希望為每個單詞構建一個稠密表示的向量，使其與出現在相似上下文中的單詞向量相似。

詞向量表示

  • 詞向量(word vectors)有時被稱為詞嵌入(word embeddings)或詞表示(word representations)。
  • 稠密詞向量是分散式表示(distributed representation)。

2.2 Word2vec原理介紹

Word2vec (Mikolov et al. 2013)是一個學習詞向量表徵的框架。

Word2vec原理介紹

核心思路如下：

  • 基於海量文本語料庫構建
  • 辭彙表中的每個單詞都由一個向量表示（學習完成後會固定）
  • 對應語料庫文本中的每個位置 \(t\)，有一個中心詞 \(c\)和一些上下文(「外部」)單詞 \(o\)
  • 使用 \(c\)和 \(o\)的詞向量來計算概率 \(P(o|c)\)，即給定中心詞推斷上下文辭彙的概率（反之亦然）
  • 不斷調整詞向量來最大化這個概率

下圖為窗口大小 \(j=2\)時的 \(P\left(w_{t+j} | w_{t}\right)\)，它的中心詞為 \(into\)

Word2vec原理介紹

下圖為窗口大小 \(j=2\)時的 \(P\left(w_{t+j} | w_{t}\right)\)，它的中心詞為 \(banking\)

Word2vec原理介紹

3.Word2vec 目標函數

3.1 Word2vec目標函數

我們來用數學表示的方式，對word2vec方法做一個定義和講解。

3.1.1 似然函數

對於每個位置 \(t=1, \cdots, T\)，在大小為 \(m\)的固定窗口內預測上下文單詞，給定中心詞 \(w_j\)，似然函數可以表示為：

\[Likelihoood = L(\theta) = \prod^{T}_{t=1} \prod_{-m \leq j \leq m \atop j \neq 0} P(w_{t+j} | w_{t} ; \theta)
\]

上述公式中， \(\theta\)為模型包含的所有待優化權重變數

3.1.2 目標函數

對應上述似然函數的目標函數 \(J(\theta)\)可以取作(平均)負對數似然：

\[J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} | w_{t} ; \theta\right)
\]

Word2vec目標函數

注意：

  • 目標函數 \(J(\theta)\)有時也被稱為「代價函數」或「損失函數」
  • 最小化目標函數 \(\Leftrightarrow\)最大化似然函數（預測概率/精度），兩者等價

補充解讀：

  • 上述目標函數中的log形式是方便將連乘轉化為求和，負號是希望將極大化似然率轉化為極小化損失函數的等價問題
  • 在連乘之前使用log轉化為求和非常有效，特別是做優化時
\[\log \prod_i x_i = \sum_i \log x_i
\]

得到目標函數後，我們希望最小化目標函數，那我們如何計算 \(P(w_{t+j} | w_{t} ; \theta)\)？

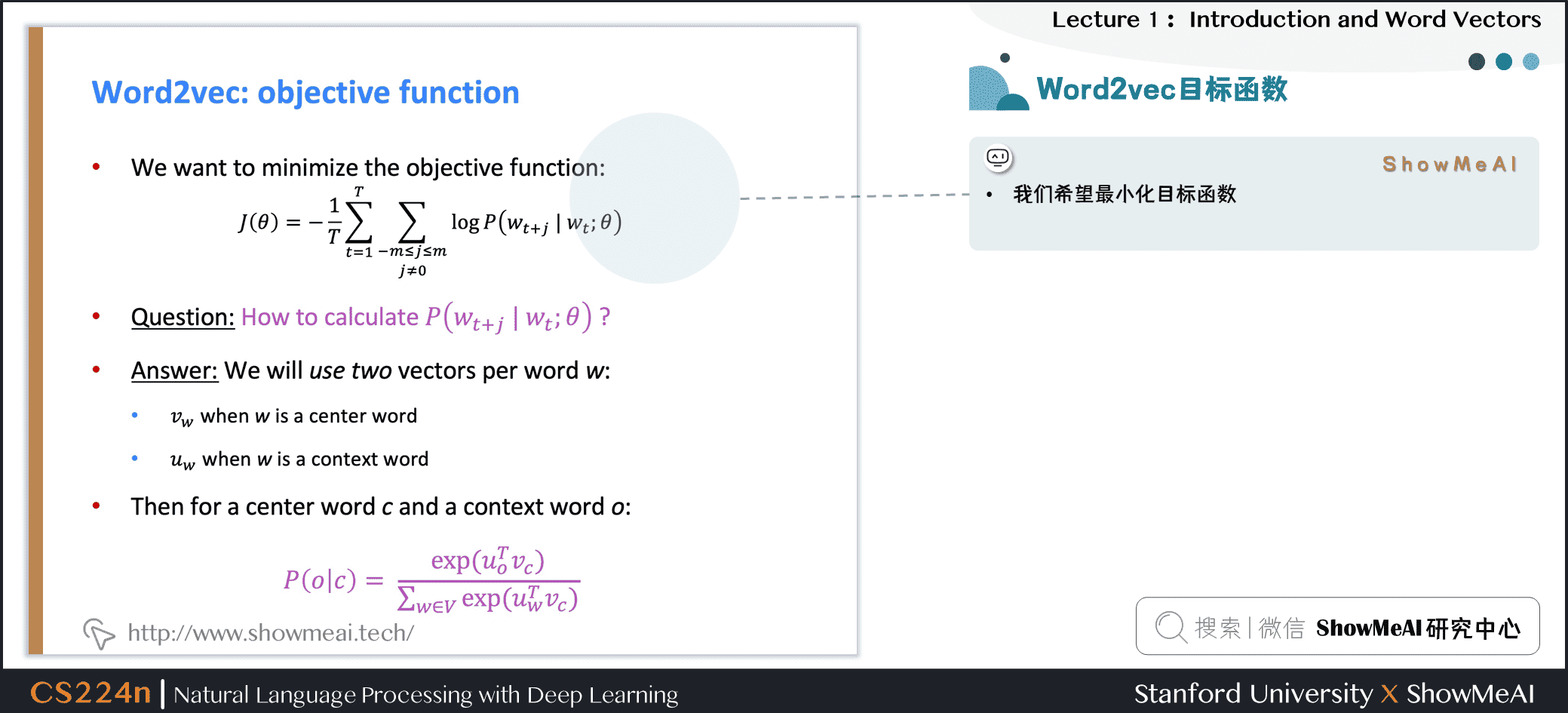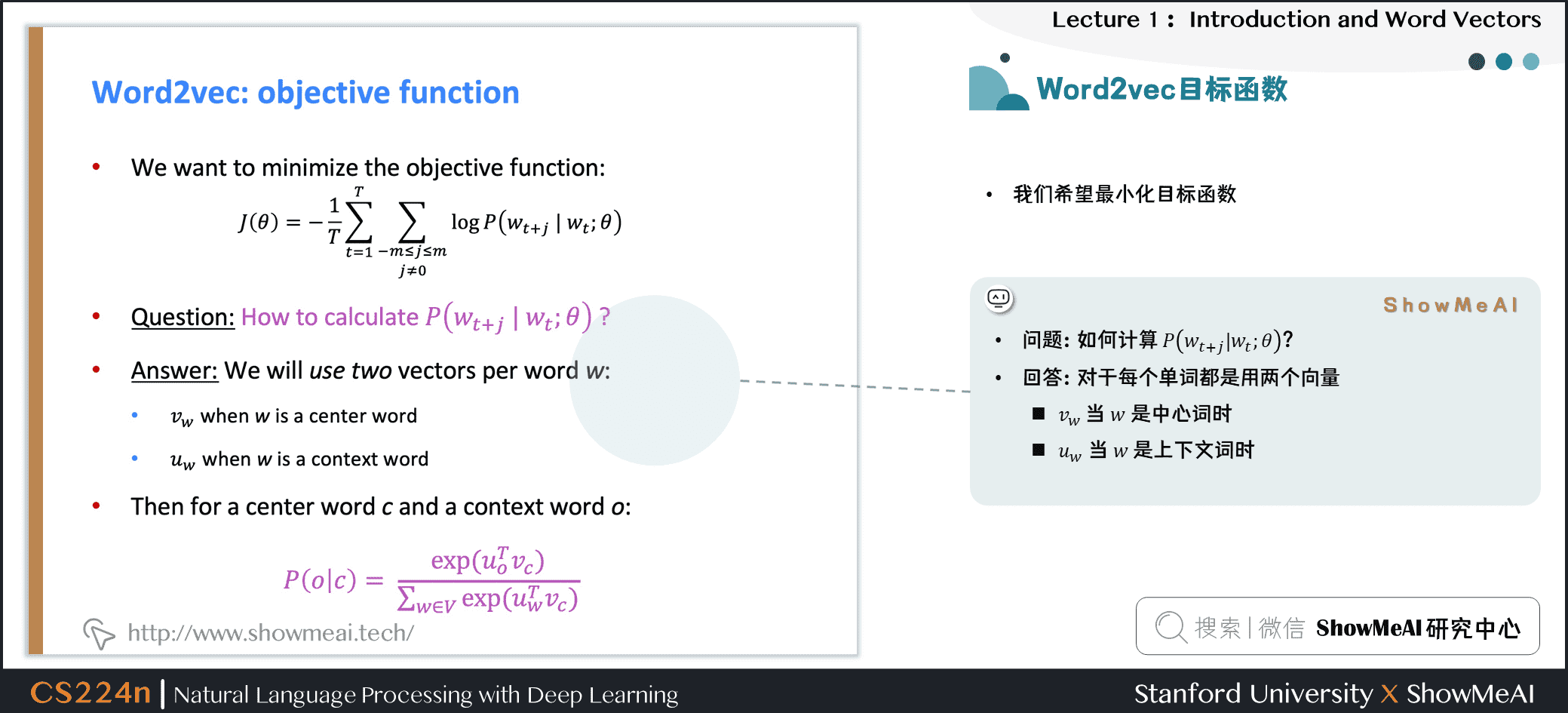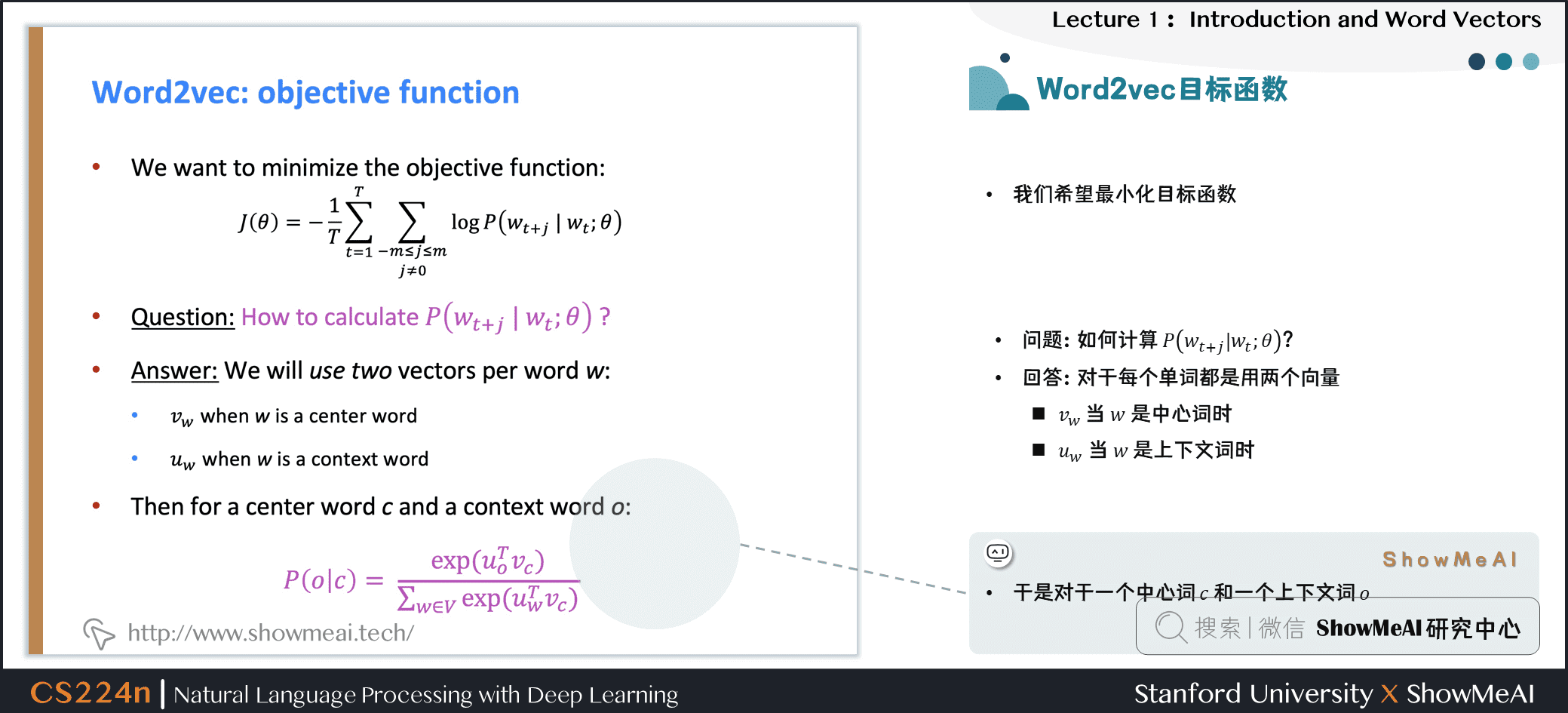
Word2vec目標函數

對於每個詞 \(w\)都會用兩個向量：

  • 當 \(w\)是中心詞時，我們標記詞向量為 \(v_w\)
  • 當 \(w\)是上下文詞時，我們標記詞向量為 \(u_w\)

則對於一個中心詞 \(c\)和一個上下文詞 \(o\)，我們有如下概率計算方式：

\[P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}
\]

Word2vec目標函數

對於上述公式，ShowMeAI做一點補充解讀：

  • 公式中，向量 \(u_o\)和向量 \(v_c\)進行點乘
  • 向量之間越相似，點乘結果越大，從而歸一化後得到的概率值也越大
  • 模型的訓練正是為了使得具有相似上下文的單詞，具有相似的向量
  • 點積是計算相似性的一種簡單方法，在注意力機制中常使用點積計算Score，參見ShowMeAI文章[C5W3] 16.Seq2Seq序列模型和注意力機制

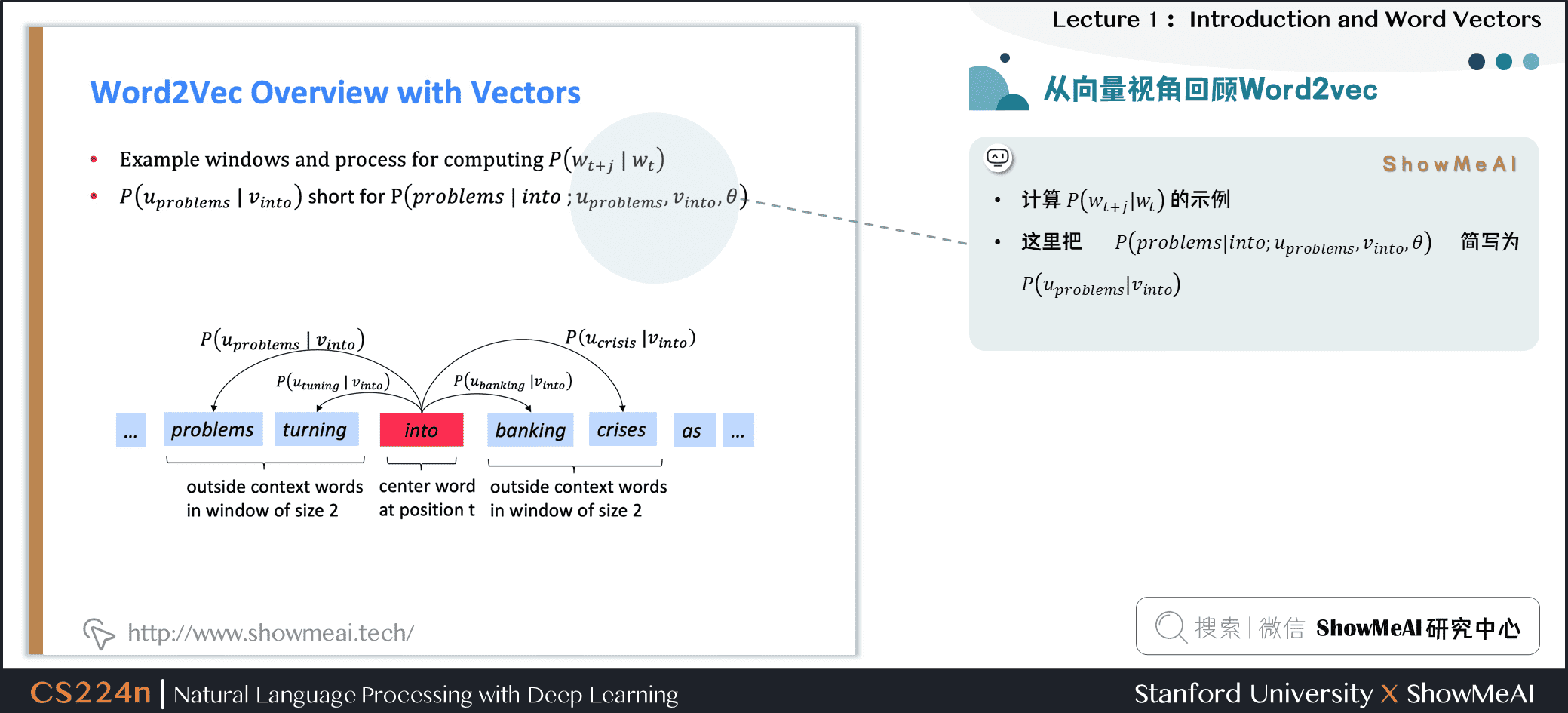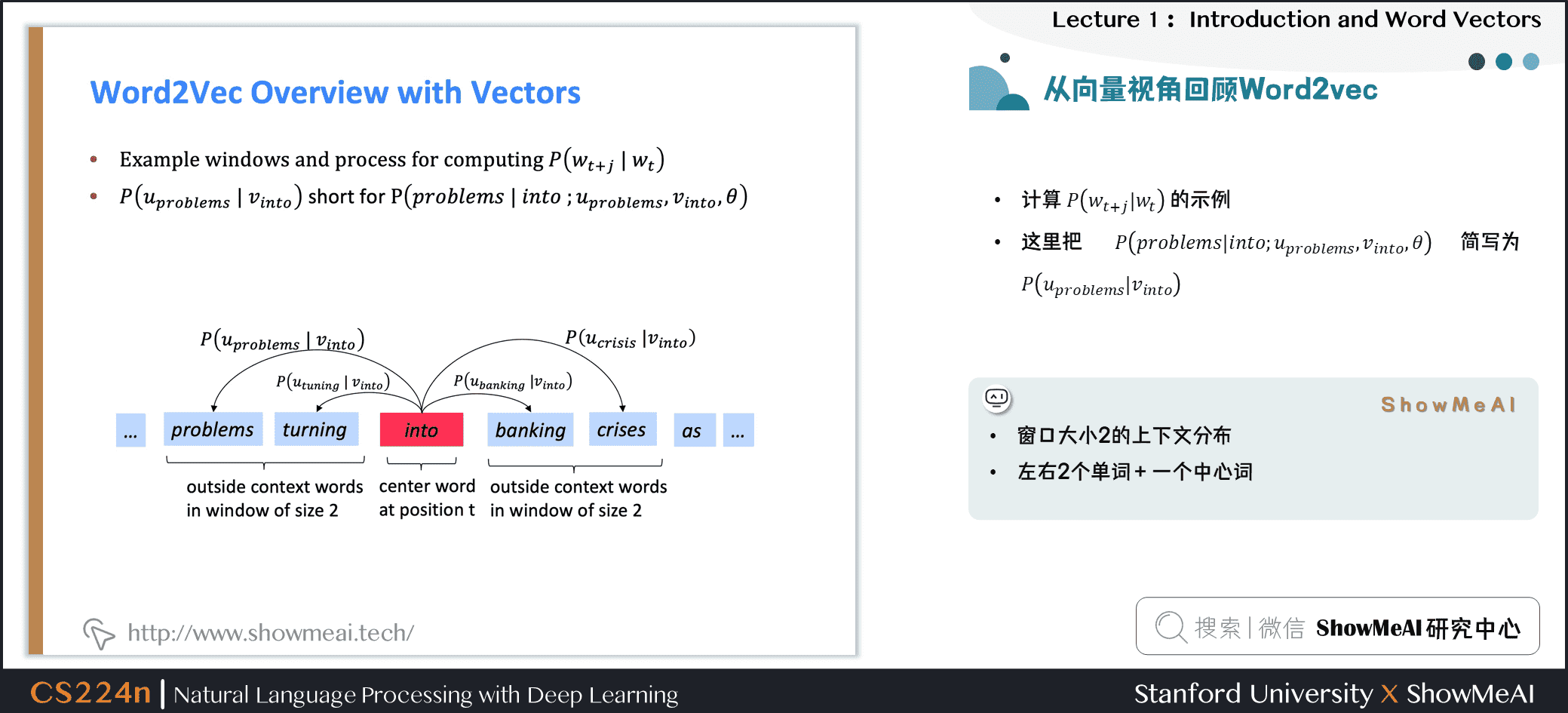
3.2 從向量視角回顧Word2vec

下圖為計算 \(P(w_{t+j} |w_{t})\)的示例，這裡把 \(P(problems|into; u_{problems},v_{into},\theta)\)簡寫為 \(P(u_{problems} | v_{into})\)，例子中的上下文窗口大小2，即「左右2個單詞+一個中心詞」。

從向量視角回顧Word2vec

4.Word2vec prediction function

4.1 Word2vec預測函數

回到上面的概率計算，我們來觀察一下

\[P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}
\]

  • 取冪使任何數都為正
  • 點積比較 \(o\)和 \(c\)的相似性 \(u^{T} v=u . v=\sum_{i=1}^{n} u_{i} v_{i}\)，點積越大則概率越大
  • 分母：對整個辭彙表進行標準化，從而給出概率分布

Word2vec預測函數

這裡有一個softmax的概率，softmax function \(\mathbb{R}^{n} \in \mathbb{R}^{n}\)示例：

將任意值 \(x_i\)映射到概率分布 \(p_i\)

\[\operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i}
\]

其中對於名稱中soft和max的解釋如下（softmax在深度學習中經常使用到）：

  • max：因為放大了最大的概率
  • soft：因為仍然為較小的 \(x_i\)賦予了一定概率

4.2 word2vec中的梯度下降訓練細節推導

下面是對於word2vec的參數更新迭代，應用梯度下降法的一些推導細節，ShowMeAI寫在這裡做一點補充。

首先我們隨機初始化 \(u_{w}\in\mathbb{R}^d\)和 \(v_{w}\in\mathbb{R}^d\)，而後使用梯度下降法進行更新

\[\begin{aligned}
\frac{\partial}{\partial v_c}\log P(o|c) &=\frac{\partial}{\partial v_c}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=\frac{\partial}{\partial v_c}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=\frac{\partial}{\partial v_c}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}
\end{aligned}
\]

偏導數可以移進求和中，對應上方公式的最後兩行的推導

\(\frac{\partial}{\partial x}\sum_iy_i = \sum_i\frac{\partial}{\partial x}y_i\)

我們可以對上述結果重新排列如下，第一項是真正的上下文單詞，第二項是預測的上下文單詞。使用梯度下降法，模型的預測上下文將逐步接近真正的上下文。

\[\begin{aligned}
\frac{\partial}{\partial v_c}\log P(o|c)
&=u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=u_o-\sum_{w\in V}\frac{\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}u_w\\
&=u_o-\sum_{w\in V}P(w|c)u_w
\end{aligned}
\]

再對 \(u_o\)進行偏微分計算，注意這裡的 \(u_o\)是 \(u_{w=o}\)的簡寫，故可知

\[\frac{\partial}{\partial u_o}\sum_{w \in V } u_w^T v_c = \frac{\partial}{\partial u_o} u_o^T v_c = \frac{\partial u_o}{\partial u_o}v_c + \frac{\partial v_c}{\partial u_o}u_o= v_c
\]

\[\begin{aligned}
\frac{\partial}{\partial u_o}\log P(o|c)
&=\frac{\partial}{\partial u_o}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=\frac{\partial}{\partial u_o}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=\frac{\partial}{\partial u_o}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=v_c-\frac{\sum\frac{\partial}{\partial u_o}\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=v_c – \frac{\exp(u_o^Tv_c)v_c}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=v_c – \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}v_c\\
&=v_c – P(o|c)v_c\\
&=(1-P(o|c))v_c
\end{aligned}
\]

可以理解，當 \(P(o|c) \to 1\)，即通過中心詞 \(c\)我們可以正確預測上下文詞 \(o\)，此時我們不需要調整 \(u_o\)，反之，則相應調整 \(u_o\)。

關於此處的微積分知識，可以查閱ShowMeAI的教程圖解AI數學基礎文章圖解AI數學基礎 | 微積分與最優化。

word2vec中的梯度下降訓練細節推導

  • 訓練模型的過程，實際上是我們在調整參數最小化損失函數。
  • 如下是一個包含2個參數的凸函數，我們繪製了目標函數的等高線。

4.3 訓練模型：計算所有向量梯度

訓練模型：計算所有向量梯度

\(\theta\)代表所有模型參數，寫在一個長的參數向量里。

在我們的場景匯總是 \(d\)維向量空間的 \(V\)個辭彙。

5.影片教程

可以點擊 B站 查看影片的【雙語字幕】版本

6.參考資料

ShowMeAI系列教程推薦

NLP系列教程文章

斯坦福 CS224n 課程帶學詳解

Tags:

VirMach 便宜 VPS

QNews

QNews