求解三角系統-從理論到程式碼優化

• 2022 年 3 月 17 日
• 筆記
• 數值計算, 高性能計算

理論

在求解n維線性系統 \(Ax=b\) ,我們通常將因子\(A\)分解為兩個三角矩陣，即 \(A=LU\) :

• \(L\) 是下三角，其中 \(L=[l_{i,j}]\) , 並滿足當\(j>i\) 時，\(l_{i,j}=0\) 和 \(l_{i,i}=1\) 。
• \(U\) 是上三角，其中 \(U=[u_{i,j}]\) ,且當 \(i>j\) 時， \(u_{i,j}=0\) 。

從而使得求解 \(Ax=b\) ，變成了求解 \(L(Ux)=b\) :

• 正向替換為: \(Ly=b\) 。
• 反向替換為： \(Ux=y\) 。

直接求解 \(A\) 的複雜度為 \(O(n^3)\) ，但是求解三角系統的複雜度為 \(O(n^2)\) 。

推導正向替換

由公式 \(Ly=b\) 展開可得：

求出對角元素:

公式和演算法

由上面推到過程可得，對於 \(k=1,2,…,n\) ：

偽程式碼演算法實現：

for k from 1 to n do:
    y[k]=b[k];
    for i from 1 to k-1 do:
        y[k]=y[k]-l[k][i]*y[i];

反向替換過程類似

程式碼實現和優化

準備

編譯器

• MSVC2019

原始程式碼

根據上文中的公式，可以很快寫出C語言程式碼如下：

void solve_triangular_system_swapped( int n, double **L, double *b, double *y ){
    for(int i=0;i<n;++i){
        y[i]=b[i];
        for(int j=0;j<i;++j){
            y[i]=y[i]-y[j]*L[i][j];
        }
    }
}

Pipeline 優化

三種典型的Pipeline：

1. 加速多條指令。
2. 加速單條指令。
3. 接續指令流水（指將電腦指令處理過程拆分為多個步驟，並通過多個硬體處理單元並行執行來加快指令執行速度）。

第三種Pipline，通常情況下每個指令長度不一。

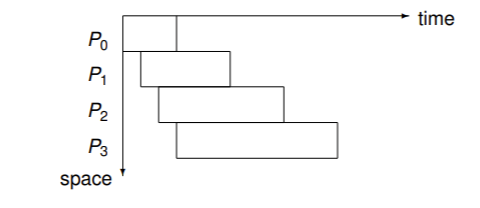
對演算法進行Pipeline分析

傳統指令Pipeline

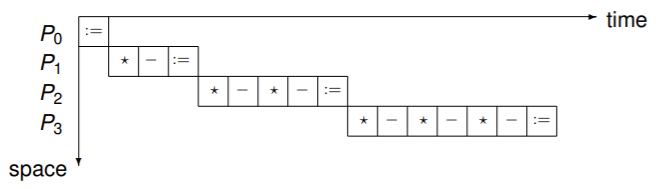
第三種Pipeline

使 \(y_1\) 在下一個流水中可用：

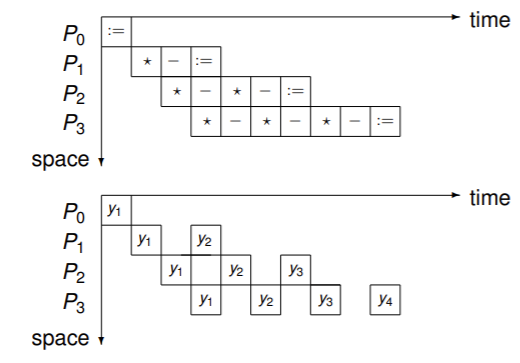
因此我們需要重寫演算法和公式

以 \(Ly=b\) 前五步為例：

1. \(y:=b\)

2. \(\begin{array}{l} y_2:=y_2-l_{2,1}*y_1;\\
   y_3:=y_3-l_{3,1}*y_1;\\
   y_4:=y_4-l_{4,1}*y_1;\\
   y_5:=y_5-l_{5,1}*y_1;\\
   \end{array}\)

3. \(\begin{array}{l} y_3:=y_3-l_{3,2}*y_2;\\
   y_4:=y_4-l_{4,2}*y_2;\\
   y_5:=y_5-l_{5,2}*y_2;
   \end{array}\)

4. \(\begin{array}{l} y_4:=y_4-l_{4,3}*y_3;\\
   y_5:=y_5-l_{5,3}*y_3;
   \end{array}\)

即：

y:=b;
for i from 2 to n do
    for j from i to n do
        y_j=y_j-l[j,i-1]*y_{i-1};

由偽程式碼可寫C語言程式碼：

void solve_triangular_system_swapped( int n, double **L, double *b, double *y )
{
    for(int i=0; i<n; i++) y[i] = b[i];
    for(int i=1; i<n; i++)
    {
        for(int j=i; j<n; j++)
            y[j] = y[j] - L[j][i-1]*y[i-1];
    }
}

優化結果

VC++編譯優化參數為\Od

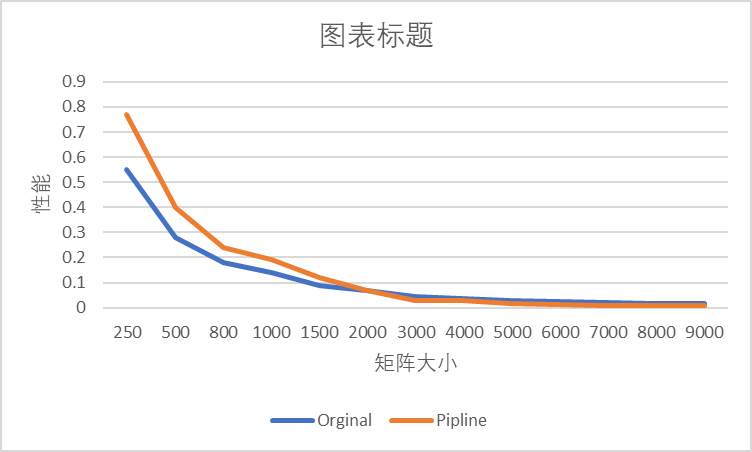
總結

1. 使用Pipline可以在矩陣規模較小時，帶來性能上的提升。
2. 矩陣規模增大時(本機為2000)，由於程式碼非快取友好程式碼，性能將比原始程式碼要差。

Unroll

使用循環展開對程式的性能進行優化也是常用的手段。循環展開層數取決於CPU邏輯暫存器的數量。因為Pipline在處理大矩陣時，性能較差，其次在\O1 優化的情況下原始程式碼有著和Pipline優化後相仿的性能，因此這裡只對原始程式碼進行Unroll。

    int j = 0, i = 0;
    for (i = 0; i < n; ++i) {
        y[i] = b[i];
        for (j = 0; j < i; j += 4) {
            y[i] = y[i] - y[j] * L[i][j];
            y[i] = y[i] - y[j + 1] * L[i][j + 1];
            y[i] = y[i] - y[j + 2] * L[i][j + 2];
            y[i] = y[i] - y[j + 3] * L[i][j + 3];
        }
        for (; j < i; j++) {
            y[i] = y[i] - y[j] * L[i][j];
        }
    }

優化結果

VC++編譯優化參數為\O1

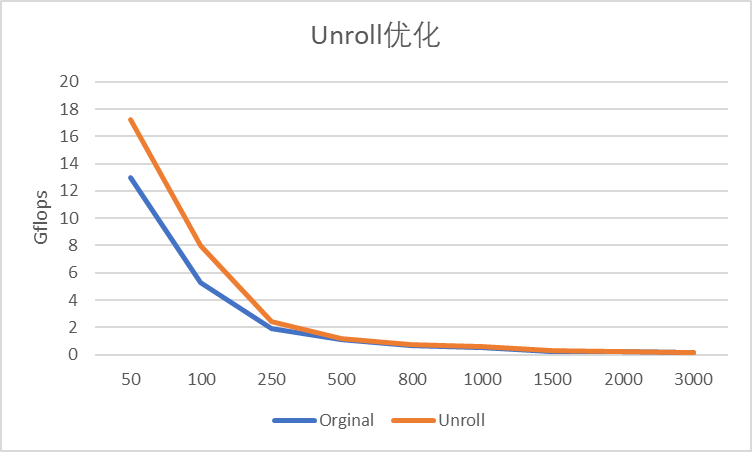
結論

1. 當矩陣規模小時，Unroll可以帶來可觀的性能提升。
2. 當矩陣規模增大時，當前程式主要受制於訪存（由Roofline模型亦可得到相同結論），可以優化空間有限。
3. 當前演算法無法使用SIMD指令來獲得加速增益。

並行優化

使用多個執行緒來提升性能：

void solve_triangular_system_swapped_omp( int n, double **L, double *b, double *y )
{
    for(int i=0; i<n; i++) y[i] = b[i];
    for(int i=1; i<n; i++)
    {
        #pragma omp parallel shared(L,y) private(j)
        {
            #pragma omp for
            for(int j=i; j<n; j++)
                y[j] = y[j] - L[j][i-1]*y[i-1];
        }
    }
}