【讀書筆記】貝葉斯原理

頻率學派和貝葉斯學派
| 頻率學派 | 貝葉斯學派 | |
|---|---|---|
| 概率的定義 | 事件重複若干次後頻率的極限 | 事件發生的不確定程度 |
| 判別方法 | 沒有先驗概率;要求事件是可重複的 | 有先驗概率 |
| 描述不確定程度 | 置信區間或p值 | 後驗概率 |
| 求解方法(測量全世界大學生的平均身高) | 認為這是一個確定值,用極大似然估計求解 | 認為不同值都有一個概率,用貝葉斯定理求解後驗概率 |
條件概率的來源
-
除了邏輯學中正誤確定的論斷,還應考慮有不確定可信度的論斷。類似於\(B\rightarrow A\)的邏輯推斷,當我們得到新資訊時,相關論斷的可信度也應發生變化。比如,對於\(B\rightarrow A\),當\(B\)的可信度提高時,\(A\)也應該提高(條件概率);當\(A\)的可信度提高時,有時\(B\)也會提高(貝葉斯方法)
-
推導出唯一概率系統的考克斯公理

-
概率論是常識推斷的定量表述
類比邏輯論斷\(B\rightarrow A\),先驗概率\(P(B)\)為假設\(B\)成立的概率,條件概率\(P(A|B)\)為推斷「\(\rightarrow\)」成立的概率,聯合概率\(P(\mathbf{A}, \mathbf{B})\)為兩個假設同時成立的概率
-
條件概率的計算式來源
- 根據第三條公理可知,聯合事件發生的概率是由單一事件概率與條件概率決定的
- 直觀上來看,\(P(A|B)\)與\(P(B)\)越大,聯合事件發生的概率越大
- 乘法能保證概率值始終在\([0,1]\)區間
- 因此有\(P(\mathbf{A}, \mathbf{B})=P(\mathbf{A} \mid \mathbf{B}) P(\mathbf{B})\)
貝葉斯公式
-
核心:利用變數間的相關性,用新得到的可觀測變數的資訊來更新對不可觀測變數的估計
- 當某一觀測變數發生後,另一不可觀測量的發生概率如何發生改變
- 更新前的估計就是先驗概率
-
舉例
| 不可觀測量\(A\) | 可觀測量\(B\) | 正向概率 \(P(B\mid A)\) | 逆向概率 \(P(A\mid B)\) | |
|---|---|---|---|---|
| 發動機 | 發動機是不是壞了 | 聲音不對 | 壞了過後的聲音是不是這個聲音? | 聽到這個聲音,發動機是不是壞了? |
| 抽球 | 盒子中不同顏色小球的比例 | 摸出小球的顏色 | 摸出小球可能是什麼顏色? | 盒中小球的顏色比例? |
| 女神 | 女神是否喜歡你 | 女神對你笑 | 女神喜歡你的話,對你笑的概率有大? | 女神如果對你笑了,喜歡你嗎? |
-
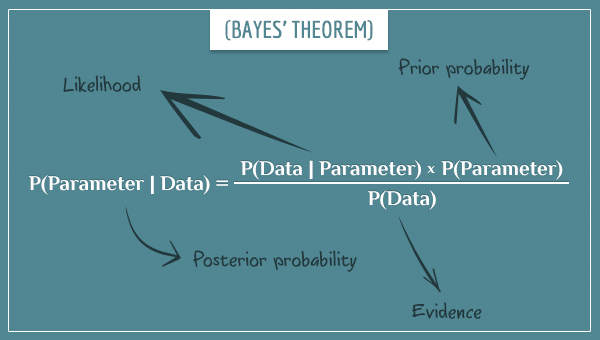
公式:\(P(A \mid B)= \frac{P(B \mid A)P(A)}{P(B)}\)
可以理解為\(P(A,B) = P(A \mid B)P(B)=P(A)P(B \mid A)\),同一相關關係的不同描述角度
-
求解:
以女神為例,要計算\(P(A \mid B)\),帶入公式計算其餘各項即可
- \(P(A)\):女神之前就喜歡你嗎?如果是路人,還是設置為50%的概率吧
- \(P(B|A)\):喜歡一個人大概率會笑吧,可以設置為60%
- \(P(B)\):女神平時傻笑嗎?高冷的話可以設置為40%
計算後可得,喜歡你的先驗概率提升為75%了!感謝貝葉斯!
貝葉斯公式的應用
- 垃圾郵件篩選(垃圾郵件、敏感字詞)
- 疾病檢測(得病,報告)
- 貝葉斯方法可能是解決小樣本學習的關鍵方法




