【數據結構與演算法】股票系列通解
121. 買賣股票的最佳時機
給定一個數組 prices ,它的第 i 個元素 prices[i] 表示一支給定股票第 i 天的價格。
你只能選擇 某一天 買入這隻股票,並選擇在 未來的某一個不同的日子 賣出該股票。設計一個演算法來計算你所能獲取的最大利潤。
返回你可以從這筆交易中獲取的最大利潤。如果你不能獲取任何利潤,返回 0 。
示例 1:
輸入:[7,1,5,3,6,4]
輸出:5
解釋:在第 2 天(股票價格 = 1)的時候買入,在第 5 天(股票價格 = 6)的時候賣出,最大利潤 = 6-1 = 5 。
注意利潤不能是 7-1 = 6, 因為賣出價格需要大於買入價格;同時,你不能在買入前賣出股票。
示例 2:
輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這種情況下, 沒有交易完成, 所以最大利潤為 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
普通 dp:
-
一般狀態:
dp[i][0]:第i天的利潤,0表示不持有股票(從未持有過,或已賣出)dp[i][1]:第i天的利潤,1表示正在持有股票(之前也持有,或第i天才買入股票)
-
初始狀態
dp[0][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0dp[0][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格
-
狀態轉移方程
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][1] = Math.max(dp[i - 1][1], - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入。(這裡注意不能寫成dp[i][1] = Math.max(dp[i - 1][1], dp[i-1][0] - prices[i]),因為該題只能買賣一次,買之前的利潤都為 0)

class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[][] = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], - prices[i]);
}
return dp[n - 1][0];
}
}
時間複雜度 O(n),空間複雜度 O(n)
狀態壓縮:
第 i 天的最大收益只和第 i - 1 天的最大收益相關,空間複雜度可以降到 O(1)。去掉一維即可。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[] = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[0] = Math.max(dp[0], dp[1] + prices[i]);
dp[1] = Math.max(dp[1], - prices[i]);
}
return dp[0];
}
}
時間複雜度 O(n),空間複雜度 O(1)
單調性的角度
用一個變數記錄一個歷史最低價格 minprice,我們就可以假設自己的股票是在那天買的。那麼我們在第 i 天賣出股票能得到的利潤就是 prices[i] - minprice
public class Solution {
public int maxProfit(int prices[]) {
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < minprice) {
minprice = prices[i];
} else if (prices[i] - minprice > maxprofit) {
maxprofit = prices[i] - minprice;
}
}
return maxprofit;
}
}
時間複雜度 O(n),空間複雜度 O(1)`
122. 買賣股票的最佳時機 II
[LeetCode 122. 買賣股票的最佳時機 II](//leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/)
給定一個數組 prices ,其中 prices[i] 表示股票第 i 天的價格。
在每一天,你可能會決定購買和/或出售股票。你在任何時候 最多 只能持有 一股 股票。你也可以購買它,然後在 同一天 出售。
返回 你能獲得的 最大 利潤 。
示例 1:
輸入: prices = [7,1,5,3,6,4]
輸出: 7
解釋: 在第 2 天(股票價格 = 1)的時候買入,在第 3 天(股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5-1 = 4 。
隨後,在第 4 天(股票價格 = 3)的時候買入,在第 5 天(股票價格 = 6)的時候賣出, 這筆交易所能獲得利潤 = 6-3 = 3 。
示例 2:
輸入: prices = [1,2,3,4,5]
輸出: 4
解釋: 在第 1 天(股票價格 = 1)的時候買入,在第 5 天 (股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接連購買股票,之後再將它們賣出。因為這樣屬於同時參與了多筆交易,你必須在再次購買前出售掉之前的股票。
示例 3:
輸入: prices = [7,6,4,3,1]
輸出: 0
解釋: 在這種情況下, 沒有交易完成, 所以最大利潤為 0。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
普通 dp:
-
一般狀態:
dp[i][0]:第i天的利潤,0表示不持有股票(從未持有過,或已賣出)dp[i][1]:第i天的利潤,1表示正在持有股票(之前也持有,或第i天才買入股票)
-
初始狀態
dp[0][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0dp[0][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格
-
狀態轉移方程
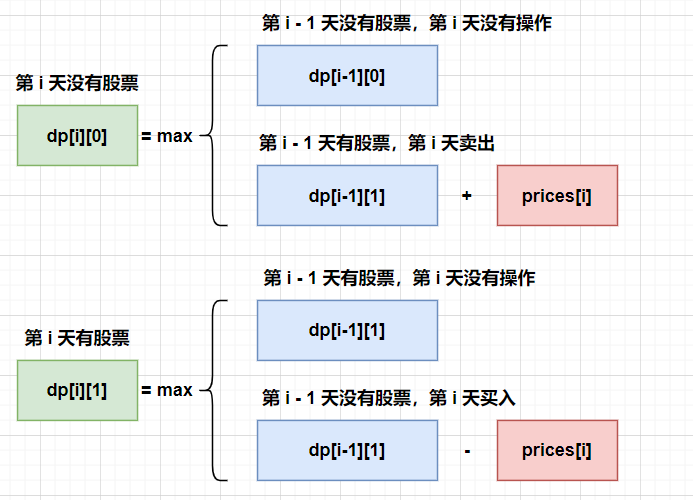
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[][] = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}
時間複雜度 O(n),空間複雜度 O(n)
狀態壓縮:
第 i 天的最大收益只和第 i - 1 天的最大收益相關,空間複雜度可以降到 O(1)。去掉一維即可。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[] = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[0] = Math.max(dp[0], dp[1] + prices[i]);
dp[1] = Math.max(dp[1], dp[0] - prices[i]);
}
return dp[0];
}
}
時間複雜度 O(n),空間複雜度 O(1)
單調性

關鍵詞是 不限制次數 ,一個處理方法就是只要後一天股票價格高於前一天,那就在前一天買進,後一天賣出,對所有利潤求和得到總利潤。
轉化成函數中求所有單獨遞增段的增加值的總和。
class Solution {
public int maxProfit(int[] prices) {
int ans = 0;
for(int i = 0; i < prices.length - 1; i++) {
if(prices[i] < prices[i + 1]) {
ans += prices[i + 1] - prices[i];
}
}
return ans;
}
}
時間複雜度 O(n),空間複雜度 O(1)`
123. 買賣股票的最佳時機 III
給定一個數組,它的第 i 個元素是一支給定的股票在第 i 天的價格。
設計一個演算法來計算你所能獲取的最大利潤。你最多可以完成 兩筆 交易。
注意:你不能同時參與多筆交易(你必須在再次購買前出售掉之前的股票)。
示例 1:
輸入:prices = [3,3,5,0,0,3,1,4]
輸出:6
解釋:在第 4 天(股票價格 = 0)的時候買入,在第 6 天(股票價格 = 3)的時候賣出,這筆交易所能獲得利潤 = 3-0 = 3 。
隨後,在第 7 天(股票價格 = 1)的時候買入,在第 8 天 (股票價格 = 4)的時候賣出,這筆交易所能獲得利潤 = 4-1 = 3 。
示例 2:
輸入:prices = [1,2,3,4,5]
輸出:4
解釋:在第 1 天(股票價格 = 1)的時候買入,在第 5 天 (股票價格 = 5)的時候賣出, 這筆交易所能獲得利潤 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接連購買股票,之後再將它們賣出。
因為這樣屬於同時參與了多筆交易,你必須在再次購買前出售掉之前的股票。
示例 3:
輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這個情況下, 沒有交易完成, 所以最大利潤為 0。
示例 4:
輸入:prices = [1]
輸出:0
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 105
普通 dp
-
一般狀態:
dp[i][k][0]:第i天的利潤,且第i天沒有股票(第i - 1天也沒有,但是第i天沒有任何操作;或者第i - 1天有,但是在第i天賣出了),k表示第i天進行的最大交易次數dp[i][k][1]:第i天的利潤,且第i天有股票(第i - 1天也有,但是第i天沒有任何操作;或者第i - 1天沒有,但是在第i天買入了),k表示第i天進行的最大交易次數
-
初始狀態
dp[0][1][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0,最大交易次數為1dp[0][1][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格,最大交易次數為1dp[0][2][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0,最大交易次數為2dp[0][2][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格,最大交易次數為2
-
狀態轉移方程
dp[i][2][0] = Math.max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][2][1] = Math.max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入,第i - 1天的最大交易次數比第i天的最大交易次數少1。dp[i][1][0] = Math.max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][1][1] = Math.max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入,第i - 1天的最大交易次數比第i天的最大交易次數少1。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][][] dp = new int[n][3][2];
dp[0][1][0] = 0;
dp[0][1][1] = -prices[0];
dp[0][2][0] = 0;
dp[0][2][1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][2][0] = Math.max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]);
dp[i][2][1] = Math.max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]);
dp[i][1][0] = Math.max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]);
dp[i][1][1] = Math.max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i]);
}
return dp[n - 1][2][0];
}
}
時間複雜度 O(n),空間複雜度 O(n)
狀態壓縮
第 i 天的最大收益只和第 i - 1 天的最大收益相關,空間複雜度可以降到 O(1)。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[3][2];
dp[1][0] = 0;
dp[1][1] = -prices[0];
dp[2][0] = 0;
dp[2][1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[2][0] = Math.max(dp[2][0], dp[2][1] + prices[i]);
dp[2][1] = Math.max(dp[2][1], dp[1][0] - prices[i]);
dp[1][0] = Math.max(dp[1][0], dp[1][1] + prices[i]);
dp[1][1] = Math.max(dp[1][1], dp[0][0] - prices[i]);
}
return dp[2][0];
}
}
時間複雜度 O(n),空間複雜度 O(1)
188. 買賣股票的最佳時機 IV
給定一個整數數組 prices ,它的第 i 個元素 prices[i] 是一支給定的股票在第 i 天的價格。
設計一個演算法來計算你所能獲取的最大利潤。你最多可以完成 k 筆交易。
注意:你不能同時參與多筆交易(你必須在再次購買前出售掉之前的股票)。
示例 1:
輸入:k = 2, prices = [2,4,1]
輸出:2
解釋:在第 1 天 (股票價格 = 2) 的時候買入,在第 2 天 (股票價格 = 4) 的時候賣出,這筆交易所能獲得利潤 = 4-2 = 2 。
示例 2:
輸入:k = 2, prices = [3,2,6,5,0,3]
輸出:7
解釋:在第 2 天 (股票價格 = 2) 的時候買入,在第 3 天 (股票價格 = 6) 的時候賣出, 這筆交易所能獲得利潤 = 6-2 = 4 。
隨後,在第 5 天 (股票價格 = 0) 的時候買入,在第 6 天 (股票價格 = 3) 的時候賣出, 這筆交易所能獲得利潤 = 3-0 = 3 。
提示:
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000
普通 dp
-
一般狀態:
dp[i][k][0]:第i天的利潤,且第i天沒有股票(第i - 1天也沒有,但是第i天沒有任何操作;或者第i - 1天有,但是在第i天賣出了),k表示第i天進行的最大交易次數dp[i][k][1]:第i天的利潤,且第i天有股票(第i - 1天也有,但是第i天沒有任何操作;或者第i - 1天沒有,但是在第i天買入了),k表示第i天進行的最大交易次數
-
初始狀態
dp[0][k][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0,最大交易次數為kdp[0][k][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格,最大交易次數為k
-
狀態轉移方程
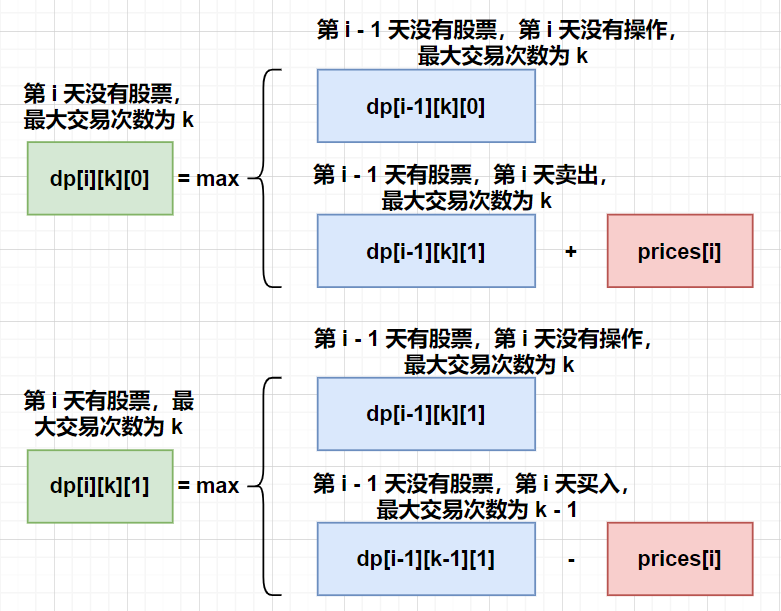
dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入,第i - 1天的最大交易次數比第i天的最大交易次數少1。

class Solution {
public int maxProfit(int k, int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int n = prices.length;
int[][][] dp = new int[n][k + 1][2];
for(int i = 1; i <= k; i++) { // 賦初值
dp[0][i][0] = 0;
dp[0][i][1] = -prices[0];
}
for(int i = 1; i < n; i++) {
for(int j = 1; j <= k ;j++) {
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
return dp[n - 1][k][0];
}
}
時間複雜度為 O(nk) 和空間複雜度為 O(nk)
狀態壓縮
第 i 天的最大收益只和第 i - 1 天的最大收益相關
class Solution {
public int maxProfit(int k, int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int n = prices.length;
int[][] dp = new int[k + 1][2];
for(int i = 1; i <= k; i++) {
dp[i][0] = 0;
dp[i][1] = -prices[0];
}
for(int i = 1; i < n; i++) {
for(int j = 1; j <= k ;j++) {
dp[j][0] = Math.max(dp[j][0], dp[j][1] + prices[i]);
dp[j][1] = Math.max(dp[j][1], dp[j - 1][0] - prices[i]);
}
}
return dp[k][0];
}
}
時間複雜度為 O(nk) 和空間複雜度為 O(k)
309. 最佳買賣股票時機含冷凍期
給定一個整數數組prices,其中第 prices[i] 表示第 i 天的股票價格 。
設計一個演算法計算出最大利潤。在滿足以下約束條件下,你可以儘可能地完成更多的交易(多次買賣一支股票):
賣出股票後,你無法在第二天買入股票 (即冷凍期為 1 天)。
注意:你不能同時參與多筆交易(你必須在再次購買前出售掉之前的股票)。
示例 1:
輸入: prices = [1,2,3,0,2]
輸出: 3
解釋: 對應的交易狀態為: [買入, 賣出, 冷凍期, 買入, 賣出]
示例 2:
輸入: prices = [1]
輸出: 0
提示:
1 <= prices.length <= 5000
0 <= prices[i] <= 1000
普通 dp
-
一般狀態:
dp[i][0]:第i天的利潤,0表示不持有股票(從未持有過,或已賣出)dp[i][1]:第i天的利潤,1表示正在持有股票(之前也持有,或第i天才買入股票)
-
初始狀態
dp[0][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0dp[0][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格
-
狀態轉移方程
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-2天沒有股票但是第i天買入。在有冷卻時間的情況下,如果在第i - 1天賣出了股票,就不能在第i天買入股票。因此,如果要在第i天買入股票,第二個狀態轉移方程中就不能使用dp[i - 1][0],而應該使用dp[i - 2][0]。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[][] = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], (i >= 2 ? dp[i - 2][0] : 0) - prices[i]);
}
return dp[n - 1][0];
}
}
時間複雜度為 O(n) 和空間複雜度為 O(n)
狀態壓縮
第 i 天的最大收益只和第 i - 1 天和第 i - 2 天的最大收益相關
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp[] = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
int pre = 0; // 記錄第 i - 2 天的利潤(無股票)
for(int i = 1; i < n; i++) {
int nextProfit0 = Math.max(dp[0], dp[1] + prices[i]);
int nextProfit1 = Math.max(dp[1], pre - prices[i]);
pre = dp[0];
dp[0] = nextProfit0;
dp[1] = nextProfit1;
}
return dp[0];
}
}
時間複雜度為 O(n) 和空間複雜度為 O(1)
714. 買賣股票的最佳時機含手續費
普通 dp
-
一般狀態:
dp[i][0]:第i天的利潤,0表示不持有股票(從未持有過,或已賣出)dp[i][1]:第i天的利潤,1表示正在持有股票(之前也持有,或第i天才買入股票)
-
初始狀態
dp[0][0] = 0:第0天不持有股票,之前也沒有買過,利潤為0dp[0][1] = -prices[0]:第0天持有股票,之前沒有買過,是第0天才買入的,利潤為-prices[0],及當日股票購入的價格
-
狀態轉移方程
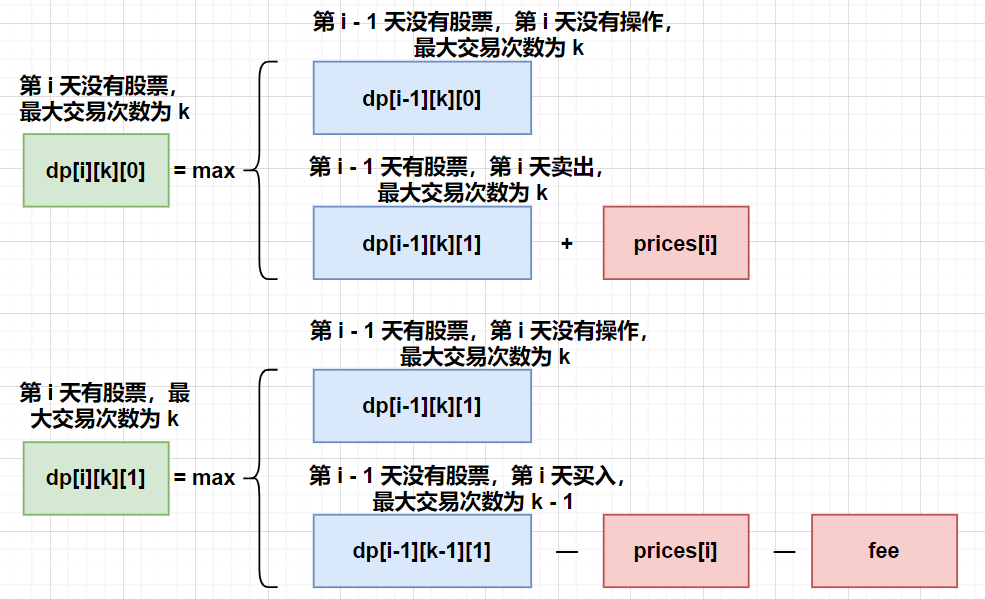
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]):第i天沒有股票,說明要麼第i-1天也沒有股票並且第i天沒有任何操作,要麼第i-1天有股票但是第i天賣出了。dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee):第i天持有股票,說明要麼第i-1天也持有股票並且第i天沒有任何操作,要麼第i-1天沒有股票但是第i天買入,同時付手續費。
class Solution {
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0] - fee;
for(int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
}
return dp[n - 1][0];
}
}
時間複雜度為 O(n) 和空間複雜度為 O(n)
狀態壓縮
第 i 天的最大收益只和第 i - 1 天的最大收益相關
class Solution {
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[] dp = new int[2];
dp[0] = 0;
dp[1] = -prices[0] - fee;
for(int i = 1; i < n; i++) {
dp[0] = Math.max(dp[0], dp[1] + prices[i]);
dp[1] = Math.max(dp[1], dp[0] - prices[i] - fee);
}
return dp[0];
}
}
時間複雜度為 O(n) 和空間複雜度為 O(1)
總結
從上面六個體可以總結出一個模板
dp[i][k][j]i:第i天k:可能的最大交易次數j:j = 0表示當前沒有股票;j = 1表示當前持有股票dp[i][k][0]:表示在第i天結束時,最多進行k次交易且在進行操作後持有0份股票的情況下可以獲得的最大收益;dp[i][k][1]:表示在第i天結束時,最多進行k次交易且在進行操作後持有1份股票的情況下可以獲得的最大收益。
總共涉及到三個狀態
- 買入
- 賣出
- 無操作
dp[i][k][j] 與 dp[i - 1][k - 1][j] dp[i - 1][k][j] dp[i][k - 1][j] 等子問題有關。
一般的狀態轉移方程如下:
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
其他問題只不過是在此基礎上進行小變形,通過股票系列這幾個題可以加深對動態規劃的認識和理解,也可以有效的應對面試。
參考資料
力扣官方題解


