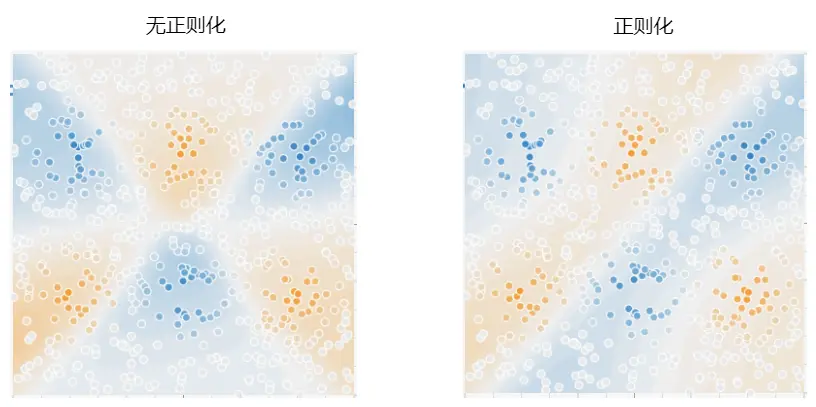
深度學習——正則化
深度學習——正則化
作者:Oto_G
全是自我理解,表達不嚴謹,僅供參考
本文默認正則化範數為L1範數
這是今天討論的問題:
- 為什麼融入正則的損失函數能夠防止過擬合
- 為什麼正則融入損失函數的形態是:原損失函數 + 範數
- 範數是啥
防止過擬合
過擬合,通俗來說就是,你的參數訓練的太好了,以至於這組參數只能在你的訓練數據上有好的表現 XD
遇到過擬合先冷靜下來,因為你遇到的情況可能比你想得還要糟糕,下面是產生過擬合的兩種情況,僅供參考 XD
- 給的訓練參數太多了,導致過擬合。如果是這種情況,恭喜你,今天所講的就是針對它的解決方法 ヽ(°▽°)ノ
- 訓練數據和測試數據不兼容,通俗來講,你的訓練數據或者是測試數據有問題,但你誤以為是模型過擬合了。如果是這種情況,晚安,瑪卡巴卡
好的,說完過擬合,我們回到第一個問題,為什麼融入正則的損失函數能夠防止過擬合
可以看到標題已經給出了模型過擬合後的一種解決方案,就是將你的損失函數稍加修改,把正則化這個概念引入你的損失函數
不用擔心,引入正則化非常簡單,但還是先來看下啥是正則化
首先,和正則表達式區分一下,在了解正則化前呢,請告訴自己,正則表達式和正則化沒有任何關係:P
正則化以我的理解就是,將你訓練的參數向量(矩陣)在最小化模型影響地情況下,儘可能地稀疏化
稀疏矩陣是數值計算中普遍存在的一類矩陣,主要特點是絕大部分的矩陣元素為零
假設你沒有使用正則化訓練好的參數是左圖,那麼正則化就是讓這個參數儘可能地變成右圖,甚至為一些參數直接為0
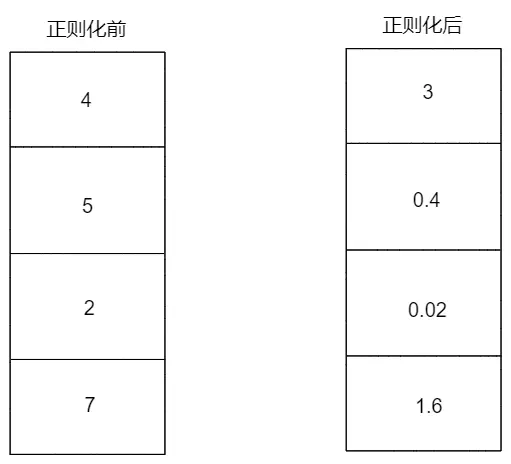
這樣之後,我們再想想,之前過擬合是由於參數太多導致的,正則化之後,部分參數的權重接近於零,那麼就相當於該參數對模型的影響大幅減小,那麼也就不會過擬合了
- 可能這時候有同學會想到,如果引入正則化導致部分參數降低了對模型的影響,會不會降低錯參數導致模型效果不佳呀?
- 答:正則化完全不會降低錯參數。首先模型的收斂還是靠損失函數決定,而正則化只是對損失函數進行線性相加,不會導致損失函數意義改變,所以訓練後的參數還是適配模型的。反過來講,正則化之所以能夠做到將參數稀疏化,又能保持適配模型,就是靠的其參與到損失函數優化過程中(直接將範數加在了損失函數後面)
正則融入損失函數的形態
接著上面一段,最後說到,正則化之所以能夠做到將參數稀疏化,又能保持適配模型,就是靠的其參與到損失函數優化過程中(直接將範數加在了損失函數後面)
這裡引出範數的概念,專業解釋可以查下權威書籍,通俗來說,舉個例子:有一個參數向量,那麼L2範數就是這個參數向量到坐標原點的歐氏距離
具體Lp的範式定義如下,xi為參數向量或矩陣

- L1範數:參數的絕對值之和
- L2範數:參數與原點的歐氏距離
而正則化就是在原來的損失函數基礎上加上L1範數(有時也會L2)乘以權重
權重(這是個超參數,需要先行給定)就是用來調整模型在泛化能力和擬合能力上的關係的,一般設0.1,根據訓練情況可以自行調整
直觀體會
進入//playground.tensorflow.org/
配置成如圖所示的狀態,紅色實線框為需要調整的地方,虛線框即為正則化選項(範數和權重),點擊左上角按鈕即可訓練。可以自行嘗試選擇不同的範數和權重,看看訓練結果會如何
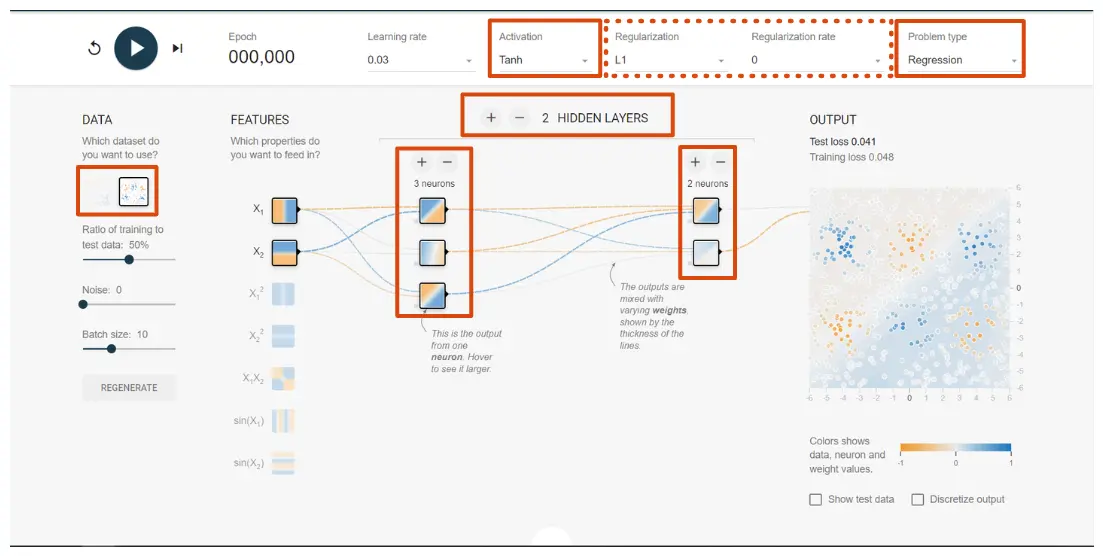
下面給出我的訓練結果