DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZ | TORCH.AUTOGRAD

torch.autograd 是PyTorch的自動微分引擎，用以推動神經網路訓練。在本節，你將會對autograd如何幫助神經網路訓練的概念有所理解。

背景

神經網路（NNs）是在輸入數據上執行的嵌套函數的集合。這些函數由參數（權重、偏置）定義，並在PyTorch中保存於tensors中。

訓練NN需要兩個步驟：

  • 前向傳播：在前向傳播中（forward prop），神經網路作出關於正確輸出的最佳預測。它使輸入數據經過每一個函數來作出預測。
  • 反向傳播：在反向傳播中（backprop），神經網路根據其預測中的誤差來調整其參數，它通過從輸出向後遍歷，收集關於函數參數的誤差的導數（梯度），並使用梯度下降優化參數。有關更多關於反向傳播的細節，參見video from 3Blue1Brownvideo from 3Blue1Brown。

在PyTorch中的使用

讓我們來看一下單個訓練步驟。對於這個例子，我們從 torchvision 載入了一個預訓練的resnet18模型。我們創建了一個隨機數據tensor，用以表示一個3通道圖片，其高和寬均為64，而其對應的 label 初始化為某一隨機值。

import torch, torchvision
model = torchvision.models.resnet18(pretrained=True)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)

接下來，我們將數據輸入模型，經過模型的每一層最後作出預測。這是前向過程。

prediction = model(data) # forward pass

我們使用模型的預測及其對應的標籤計算誤差（loss）。下一步是通過網路反向傳播誤差。當在誤差tensor上調用.backward()時，反向傳播開始。然後，Autograd計算針對每一個模型參數的梯度，並將其保存在參數的 .grad 屬性中。

loss = (prediction - labels).sum()
loss.backward() # backward pass

接下來，我們載入一個優化器，在此案例中是SGD，學習率是0.01，動量參數（momentum）是0.9。我們在優化器中註冊所有的模型參數。

optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

最後，我們調用 .step()啟動梯度下降。優化器會通過保存在 .grad 的參數梯度調整所有參數。

optim.step() # gradient descent

此時，你已擁有訓練神經網路所需的一切。以下部分詳細介紹了autograd的工作原理 – 可隨意跳過。

Autograd中的微分

讓我們來看一下 autograd是如何收集梯度的。創建兩個tensor a 和 b，並且 requires_grad=True。這向 autograd 發出訊號，跟蹤在它們上執行的每一個操作。

import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)

由 a 和 b 創建tensor Q。

\[Q = 3a^2 – b^2
\]

Q = 3*a**2 - b**2

假設 a 和 b 是一個神經網路的參數，Q 是誤差。在NN訓練中，求解關於參數的梯度，即：

\[\frac{\partial Q}{\partial a} = 9a^2
\]

\[\frac{\partial Q}{\partial b} = -2b
\]

當我們在 Q 上調用 .backward()，autograd計算以上梯度並保存在對應tensor的 .grad 屬性中。
Q.backward() 是一個向量，因此我們需要在 Q.backward() 中顯示地傳遞一個 gradient 參數。gradient 是一個和 Q相同形狀的tensor，它表示Q關於其本身的梯度，即:

\[\frac{\partial Q}{\partial Q} = 1
\]

等效地，我們還可以將Q聚合為一個標量，並隱式的向後調用，如 Q.sum().backward()

external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

梯度現在杯保存在 a.grad、b.grad 中

## 檢查收集的梯度是否正確
print(9*a**2 == a.grad)
print(-2*b == b.grad)

輸出：

tensor([True, True])
tensor([Ture, True])

選讀 – 使用 autograd 進行矢量微分

計算圖

從概念上來說，autograd在一個由Function對象組成的有向無環圖（DAG）中記錄了數據（tensors）和所有執行的操作（連同由此產生的新tensors）。在DAG中，葉節點是輸入tensors，根節點是輸出tensors。通過從根節點到葉節點跟蹤此圖，你可以使用鏈式法則自動計算梯度。

在前向過程中，autograd同時進行兩件事：

  • 執行請求的操作計算結果tensor，
  • 在DAG中保留操作的 gradient function。

在DAG根節點處調用 .backward() 時啟動反向過程。然後autograd：

  • 由每個 .grad_fn計算梯度，
  • 將梯度累積在其對應tensor的 .grad 屬性中，
  • 使用鏈式法則，將梯度一直傳播到葉節點。

下圖是以上例子中DAG的可視化表示。在該圖中，箭頭表示前向過程的方向。節點表示在前向過程中每一個操作的backward functions。藍色葉節點表示我們的tensor a 和 b。

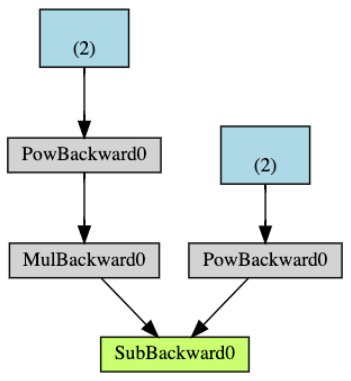
注意：DAGs在PyTorch中是動態的。需要重點注意的是：DAG是從頭開始重新創建的，在每次 .backward調用時，autograd開始填充一個新圖。這正是在模型中允許你使用控制流語句的原因。如果需要，你可以在每次迭代中更改形狀、大小和操作。

從DAG中排除

torch.autograd 跟蹤所有 requires_grad=True 的tensor上的操作。對於不要求計算梯度的tensor，requires_grad=False，並將其從梯度計算DAG中排除。

當一個操作就算只有一個輸入tensor有 requires_grad=True，其輸出的tensor仍然要計算梯度。

x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)

a = x + y
print(f"Does 'a' require gradients? : {a.requires_grad}")
b = x + z
print(f"Does 'b' require gradients? : {b.requires_grad}")

輸出：

Does `a` require gradients? : False
Does `b` require gradients?: True

在神經網路中，不計算梯度的參數通常成為凍結參數。如果你事先知道不需要這些參數的梯度，那凍結模型的一部分很有用（這通過減少autograd計算量提供了一些性能優勢）。

從DAG中排除的另一個重要的常見用法是finetuning a pretrained network

在finetune中，我們凍結模型的大部分參數，並且通常只修改分類層以對新的標籤作出預測。讓我們通過一個小例子來演示這一點。像之前一樣，我們載入一個預訓練resnet18模型，並且凍結所有參數。

from torch import nn, optim

model = torchvision.models.resnet18(pretrained=True)

# 凍結網路中的所有參數
for param in model.parameters():
    param.requires_grad = False

假設我們要在一個10標籤數據集上微調模型。在resnet中，分類層是最後的線性層 model.fc。我們可以簡單地用一個新的線性層（默認情況下未凍結）替換它作為我們的分類器。

model.fc = nn.Linear(512, 10)

模型中除了 model.fc 的所有參數均被凍結。需要計算梯度的參數僅僅是 model.fc 的權重和偏置

# 僅優化分類層
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

注意，儘管我們在優化器中註冊了所有參數，但是計算梯度（在梯度下降中更新）的參數僅是分類層的權重和偏置。

The same exclusionary functionality is available as a context manager in torch.no_grad().

Tags:

VirMach 便宜 VPS

QNews

QNews