論文解讀DEC《Unsupervised Deep Embedding for Clustering Analysis》
Abstract
在本文中,我們提出了 Deep Embedded Clustering(DEC),一種使用深度神經網路同時學習 feature representations 和 cluster assignments 的方法。DEC學習從數據空間到低維特徵空間的映射,並在其中迭代地優化聚類目標。
1. Introduction
What is Clustering???
Some questions for Clustering in unsupervised methods:
-
- What defifines a cluster?
- What is the right distance metric?
- How to effificiently group instances into clusters?
- How to validate clusters?
本文貢獻:
-
- joint optimization of deep embedding and clustering;
- a novel iterative refifinement via soft assignment;
- state-of-the-art clustering results in terms of clustering accuracy and speed.
2. Related work
聚類在機器學習的 feature selection、distance functions、grouping methods 以及 cluster validation 方面得到了廣泛研究。
Spectral clustering 及其變體最近得到了受歡迎。它們允許更靈活的距離度量,並且通常比 kmeans 表現得更好。Yang等人已經探索了 spectral clustering 和 embedding 的結合。 Tian 等人提出了一種基於 spectral clustering 的演算法,但用深度自編碼器代替特徵值分解,提高了性能,但進一步增加了記憶體消耗。
最小化 data distribution 和 embedded distribution 之間的 kullback-leibler(KL) 差異。
3. Deep embedded clustering
Consider the problem of clustering a set of $n$ points $\left\{x_{i} \in\right. X\}_{i=1}^{n} $ into $k$ clusters, each represented by a centroid $\mu_{j}$, $j=1, \ldots, k $. Instead of clustering directly in the data space $X$ , we propose to first transform the data with a nonlinear mapping $f_{\theta}: X \rightarrow Z$ , where $\theta$ are learnable parameters and $Z $ is the latent feature space. The dimensionality of $Z$ is typically much smaller than $X$ in order to avoid the “curse of dimensionality” (Bellman, 1961). To parametrize $f_{\theta}$ , deep neural networks (DNNs) are a natural choice due to their theoretical function approximation properties (Hornik, 1991) and their demonstrated feature learning capabilities (Bengio et al., 2013).
3.1. Clustering with KL divergence
3.1.1. Soft assignment
3.1.2. KL Divergence minimization
我們建議在 auxiliary target distribution 的幫助下,通過學習 high confidence assignments 來迭代地細化 clusters 。具體來說,我們的模型是通過匹配軟分配到目標分布來訓練的。為此,我們將我們的目標定義為軟分配 $q_i$ 和輔助分布 $p_i$ 之間的KL散度損失如下:
$L=\mathrm{KL}(P \| Q)=\sum \limits_{i} \sum \limits_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} \quad \quad\quad\quad (2)$
目標分布 $P$ 的選擇是 DEC 的性能的關鍵。一種簡單的方法是將超過置信閾值的數據點的每個 $p_i$ 設置為一個 $delta$ 分布(到最近的質心),而忽略其餘的。然而,由於 $q_i$ 是軟任務,所以使用較軟的概率目標更自然和靈活。
具體來說,我們希望我們的 target distribution 具有以下特性:
- strengthen predictions (i.e., improve cluster purity)
- put more emphasis on data points assigned with high confidence
- normalize loss contribution of each centroid to prevent large clusters from distorting the hidden feature space.
在我們的實驗中,我們計算 $p_i$,首先將 $q_i$ 提高到二次冪,然後按每個簇的頻率歸一化:
$p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}}\quad \quad\quad\quad (3)$
其中 $f_{j}=\sum \limits _{i} q_{i j}$ 是 soft cluster frequencies 。關於L和P的經驗性質的討論,請參考第5.1節。
3.1.3. Optimization
我們利用具有動量的隨機梯度下降(SGD)聯合優化了聚類中心 $\left\{\mu_{j}\right\} $ 和DNN參數 $\theta $。$L$ 對每個數據點 $z_i$ 和每個聚類質心 $µ_j$ 的特徵空間嵌入的梯度計算為:
$\frac{\partial L}{\partial z_{i}}=\frac{\alpha+1}{\alpha} \sum \limits _{j}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\quad \quad\quad\quad (3)$
$\frac{\partial L}{\partial \mu_{j}}=-\frac{\alpha+1}{\alpha} \sum \limits _{i}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\times\left(p_{i j}-q_{i j}\right)\left(z_{i}-\mu_{j}\right)\quad \quad\quad\quad (4)$
梯度 $\partial L / \partial z_{i}$ 然後被傳遞給DNN,並用於標準的反向傳播來計算 DNN 的參數梯度 $\partial L / \partial \theta$。為了發現集群分配,當連續兩次迭代之間改變集群分配的點小於 $tol \%$ 時,我們停止我們的過程。
3.2. Parameter initialization
到目前為止,我們已經討論了 DEC 如何處理 DNN 參數$θ$ 和簇質心 ${µ_j}$ 的初始估計。現在我們將討論參數和質心是如何初始化的。
我們使用堆疊自動編碼器(SAE)初始化DEC,因為最近的研究表明,它們在真實數據集上始終產生具有語義意義和分離良好的表示。因此,SAE學習到的無監督表示自然地促進了使用DEC進行聚類表示的學習。
我們一層一層地初始化SAE網路,每一層都是一個去噪自動編碼器,在隨機損壞後重建前一層的輸出。去噪自動編碼器是一種兩層神經網路,其定義為:
$\tilde{x} \sim \operatorname{Dropout}(x) \quad \quad\quad\quad (6)$
$h=g_{1}\left(W_{1} \tilde{x}+b_{1}\right) \quad \quad\quad\quad (7)$
$\tilde{h} \sim \operatorname{Dropout}(h) \quad \quad\quad\quad (8)$
$y=g_{2}\left(W_{2} \tilde{h}+b_{2}\right)\quad \quad\quad\quad (9)$
其中,$\operatorname{Dropout}(\cdot)$ 是一個隨機映射,它將其輸入維度的一部分隨機設置為0,$g_{1}$ and $g_{2}$ 分別為編碼層和解碼層的激活函數,$\theta=\left\{W_{1}, b_{1}, W_{2}, b_{2}\right\}$ 為模型參數。訓練是通過最小化最小二乘損失 $\|x-y\|_{2}^{2}$ 來完成的。在訓練了一層後,我們使用它的輸出有輸入來訓練下一層。我們在所有編碼器/解碼器對中使用校正線性單元(ReLUs),除了第一對的 $g_{2}$ (它需要重建可能有正負值的輸入數據,如零均值影像)和最後對的 $g_{1}$ (因此最終數據嵌入保留完整資訊)。
經過 greedy layer-wise training 後,我們將所有編碼器層和所有解碼器層,按反向層訓練順序連接起來,形成一個深度自動編碼器,然後對其進行微調,使其最小化重構損失。最終的結果是一個中間有一個瓶頸編碼層的多層深度自動編碼器。然後我們丟棄解碼器層,並使用編碼器層作為數據空間和特徵空間之間的初始映射,如 Fig. 1 所示。
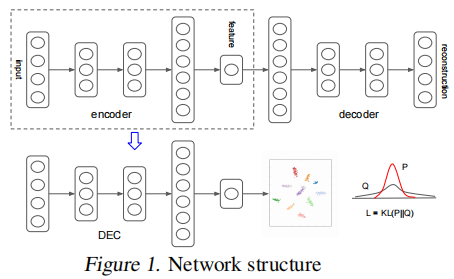
4. Experiments
4.1. Datasets
我們在一個文本數據集和兩個影像數據集上評估了所提出的方法(DEC),並將其與其他演算法包括 $k-means$、$LDGMI$ 和 $SEC$ 進行比較。$LDGMI$ 和$SEC$ 是基於 spectral clustering 的演算法,它們使用拉普拉斯矩陣和各種變換來提高聚類性能。
- MNIST:MNIST數據集由280000像素大小的70000個手寫數字組成。這些數字居中並進行尺寸歸一化(LeCun等,1998)。
- STL-10: 96 x 96彩色影像的數據集。有10個類別,每個類別有1300個樣本。它還包含100000張相同解析度的無標籤影像(Coates等,2011)。訓練自動編碼器時,我們還使用了無標籤的集合。與Doersch等人(2012)相似,我們將HOG特徵和8×8色圖連接起來,用作所有演算法的輸入。
- REUTERS: REUTERS包含大約810000個以類別樹標籤的英語新聞報道(Lewis等,2004)。我們使用了四個根類別:公司/工業,政府/社會,市場和經濟學作為標籤,並進一步修剪了由多個根類別標籤的所有文檔以得到685071個文章。然後,我們根據2000個最常見的詞幹計算tf-idf特徵。由於某些演算法無法擴展到整個Reuters數據集,因此我們還抽樣了10000個樣本的隨機子集,我們將其稱為REUTERS-10k,以進行比較。

4.2. Evaluation Metric
我們使用標準的無監督評估 metric 和 protocol 來與其他演算法進行評估和比較。對於所有的演算法,我們將聚類的數量設置為 ground-truth 類別的數量,並以無監督的聚類精度(ACC)來評估性能:
其中 $ l_{i}$ 是ground-truth label ,$c_{i}$ 是該演算法產生的聚類分配,$m$ 是將 $c_{i}$ 進行聚類映射。
4.3. Implementation
實驗參數補充,略……..
4.4. Experiment results
我們定量和定性地評估了我們的演算法的性能。在 Table 2 中,我們報告了每種演算法的最佳性能,超過9個超參數設置。

請注意,DEC的性能優於所有其他方法,有時會有很大的優勢。為了證明端到端訓練的有效性,我們還展示了在聚類過程中凍結非線性映射 $f_θ$ 的結果。
為了研究超參數的影響,我們繪製了每種方法在所有 $9$ 種設置下的準確性( Fig.2)。

我們觀察到,與 LDGMI 和 SEC 相比,DEC 在超參數範圍內更為一致。對於 DEC,超參數 $λ=40$ 在所有數據集上都給出了接近最優的性能,而對於其他演算法,最優超參數變化很大。此外,DEC可以用GPU加速處理整個 REUTERS 數據集,而第二好的演算法LDGMI和SEC則需要數月的計算時間和 TB 的記憶體。事實上,我們不能在完整的 REUTERS 數據集上運行這些方法,並在 Table 2 中報告N/A(這些方法的GPU適應不是重要的)。

在 Fig. 3 中,我們顯示了 MNIST 和 STL 中每個聚類中10張得分最高的影像。每一行對應一個 cluster,影像根據它們到 cluster center 的距離從左到右進行排序。我們觀察到,對於 MNIST,DEC 的 cluster assignment 很好地對應自然集群,除了混淆4和9,而對於STL,DEC對飛機、卡車和汽車大多是正確的,但在動物類別時,部分注意力花在姿勢上而不是類別上。
5. Discussion
5.1. Assumptions and Objective
DEC的基本假設是,初始分類器的高置信度預測大部分是正確的。為了驗證該假設對我們的任務是否成立,以及我們對 $P$ 的選擇是否具有所需的屬性,我們針對每個嵌入點 $\left|\partial L / \partial z_{i}\right|$ ,對其軟分配 $q_{ij}$ ,繪製了 $L$ 的梯度大小到隨機選擇的 MNIST 聚類 $j$(Fig4)。
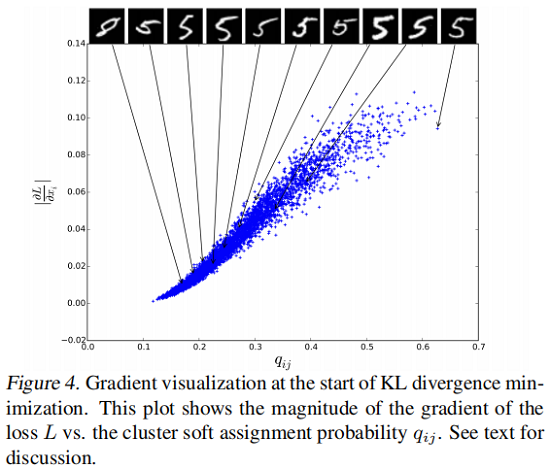
我們觀察到靠近聚類中心(較大 $q_{ij}$ )的點對梯度的貢獻更大。我們還顯示了按 $q_{ij}$ 排序的每個10個百分位數的10個數據點的原始影像。如相似度更高的實例「 5」。隨著置信度的降低,實例變得更加模稜兩可,最終變成錯誤標籤的 」8」,表明我們的假設是正確的。
5.2. Contribution of Iterative Optimization
在 Fig.5 中,我們可視化了訓練過程中 MNIST 隨機子集的嵌入式表示的進度。為了可視化,我們將 t-SNE應用於嵌入點 $z_i$。顯然,聚類之間的隔離度越來越高。 Fig.5(f) 顯示了在SGD epoch 相對應的精度如何提高。

5.3. Contribution of Autoencoder Initialization
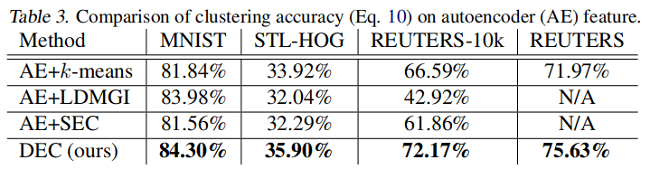
為了更好地理解每個組件的貢獻,我們在 Table 3 中展示了所有具有自編碼器特徵的演算法的性能。我們觀察到,SEC 和 LDMGI 的表現並沒有隨 autoencoder feature 而顯著變化,而 $k-means$ 有所改善,但仍低於 $DEC$ 。這證明了採用提議的 $KL$ 散度目標進行深度嵌入的能力以及微調的好處。
5.4. Performance on Imbalanced Data
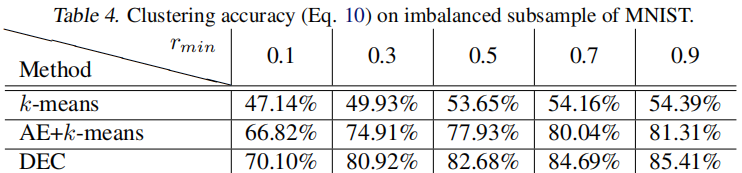
為了研究不平衡數據的影響,我們對具有不同保留率的 MNIST 子集進行了取樣。對於最小保留率 $r_{\min } $,類別 $0$ 的數據點將以 $r_{\min } $的概率保留,類別 $9$ 將以 $1$ 的概率保留,而其他類別的數據點之間則保持線性關係。結果,最大的簇將是最小簇的 $1 / r_{\min }$ 倍。從 Table 4 中我們可以看到 DEC 對於簇大小的變化具有相當強的魯棒性。我們還觀察到,在自動編碼器和 k-means 初始化(顯示為AE+k-means)之後,KL散度最小化(DEC)不斷提高了聚類精度。
5.5. Number of Clusters
到目前為止,我們已經假定給出自然簇的數量是為了簡化演算法之間的比較。但是,實際上,此數量通常是未知的。因此,需要一種確定最佳簇數的方法。為此,我們定義兩個度量:
- 標準度量,歸一化互資訊(NMI),用於評估具有不同聚類數量的聚類結果:
$N M I(l, c)=\frac{I(l, c)}{\frac{1}{2}[H(l)+H(c)]}$
其中 $I$ 是互資訊度量,$H$ 是熵。
- 泛化性(G)定義為訓練損失與驗證損失之間的比率:
$G=\frac{L_{\text {train }}}{L_{\text {validation }}}$
當訓練損失低於驗證損失時,$G$ 很小,這表明高度過擬合。
Fig. 6 顯示了當簇數從 $9$ 增加到 $10$ 時,泛化性急劇下降,這表明 $9$ 是最優的簇數。我們確實觀察到NMI得分最高為 $9$,這表明泛化性是選擇簇數的良好指標。 NMI最高是 $9$,而不是 $10$,因為 $9$ 和 $4$ 在文字上相似,DEC認為它們應該組成一個聚類。這與我們在 Fig. 3 中的定性結果非常吻合。

6. Conclusion
本文提出了深度嵌入式聚類,即DEC,一種在聯合優化的特徵空間中聚集一組數據點的演算法。DEC的工作原理是迭代優化基於KL散度的聚類目標和自訓練目標分布。我們的方法可以看作是半監督自我訓練的無監督擴展。我們的框架提供了一種方法來學習專門的表示,而沒有基本聚類成員標籤。
實證研究證明了我們所提出的演算法的有效性。DEC提供了更好的性能和魯棒性,這在無監督任務中尤其重要,因為交叉驗證是不可能的。DEC還具有數據點數量的線性複雜性的優點,這使得它可以擴展到大型數據集。
『總結不易,加個關注唄!』



