數據挖掘中的常見數據預處理方法總結

• 2022 年 1 月 5 日
• 筆記

一.基本概念

為什麼需要數據預處理：

現實世界中數據大體上都是不完整，不一致的臟數據，無法直接進行數據挖掘，或挖掘結果差強人意。為了提高數據挖掘的品質產生了數據預處理技術

數據：數據對象及其屬性的集合

屬性值是分配給屬性的數字或符號

屬性和屬性值的區別 – 相同的屬性可以映射到不同的屬性值

      　　　　　　　  – 不同的屬性可以映射到同一組值

屬性值的類型：

屬性的類型取決於它擁有以下哪些屬性：獨特性（可以判斷等於和不等）；順序；加法；乘法

標稱屬性：獨特性

序數屬性：獨特性和順序

區間屬性：獨特性、順序和加法(比如溫度)

比率屬性：所有 4 個屬性（比如長度）

數據集的類型：

記錄數據，圖數據，順序數據

順序數據舉例：

基因組序列數據；

時間-空間數據：

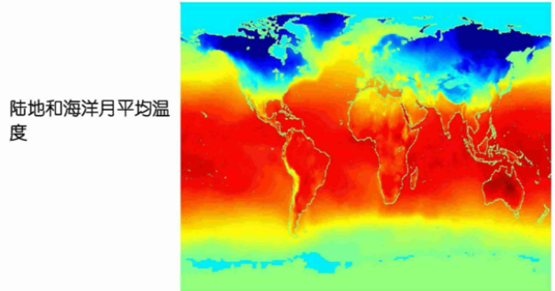
屬性的模式（眾數）是出現頻率最高的屬性值

百分位數：對於連續數據，百分位數的概念更有用，給定一個有序或連續的屬性 x 和一個 0到100 之間的數字p，第p個百分位數是一個值 x 使得 p%的值小於 x 的觀測值

第二個四分位數 = 第 50 個百分位數 = 中位數

第三個四分位數 = 第 75 個百分位數

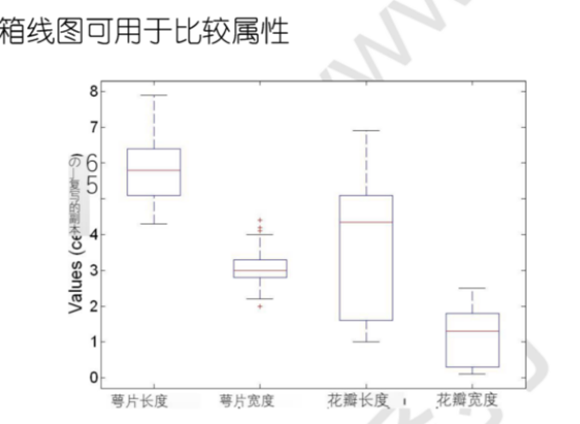
五數總結法：最低 – 第 1 個四分位數 – 中位數 – 第三個四分位數 – 最大值，可用箱形圖表示

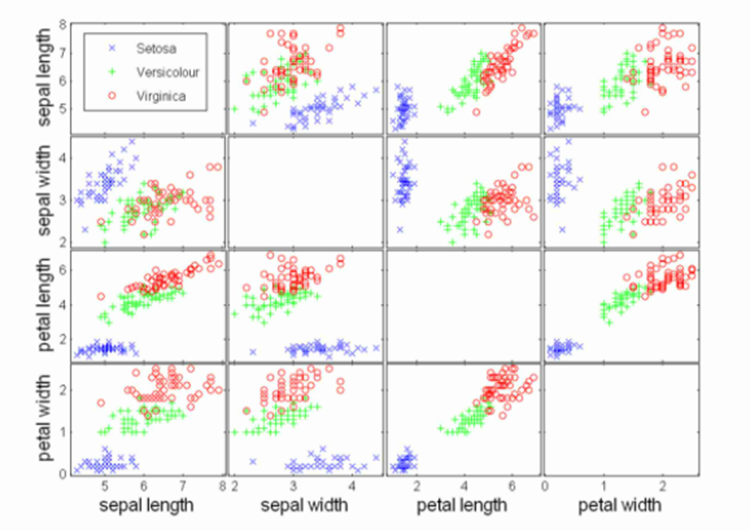
散點圖：屬性值兩兩配對作圖，可用於發現屬性間的關係

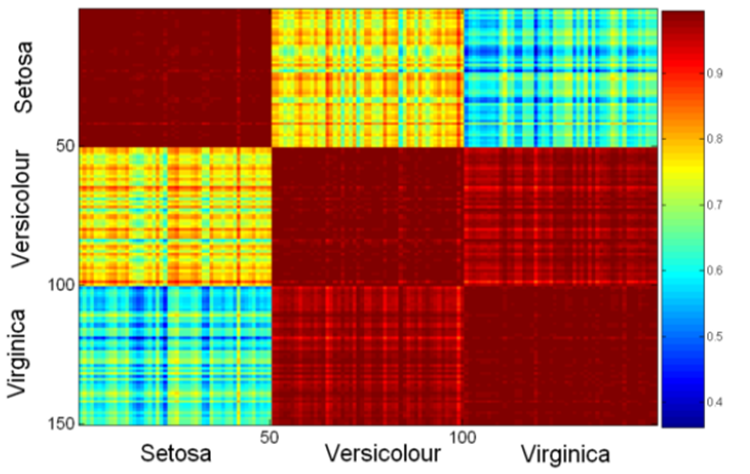
矩陣的每個值是其行坐標與列坐標的相似性

平行坐標圖：

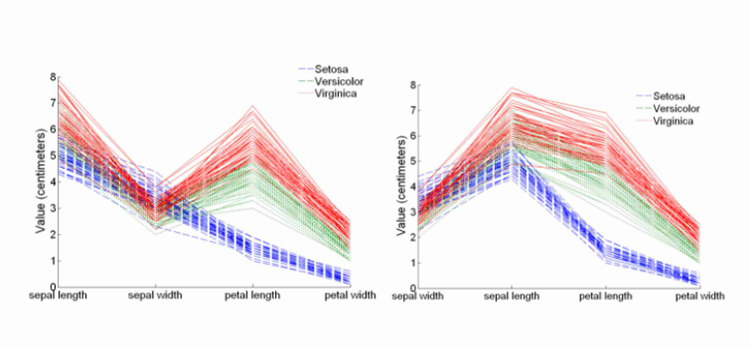
每一條折線代表一個實例，橫坐標是不同的屬性

數據品質問題：

噪音：雜訊是指對原始值的修改

異常值：異常值是具有與數據集中的大多數其他數據對象顯著不同的特徵的數據對象

缺失值

重複數據

數據品質的衡量標準:

● 準確性：正確或錯誤，準確與否

● 完整性：未記錄、不可用、……

● 一致性：一些修改但一些沒有，懸空，

● 及時性：及時更新？

● 可信度：數據正確的可信度如何？

● 可解釋性：數據有多容易被理解？

數據預處理

數據清洗 清理缺失數據： ●忽略元組：通常在缺少類標籤時完成（進行分類時）——當每個屬性的缺失值百分比變化很大時無效 ● 手動填寫缺失值：乏味+不可行？ ● 自動填寫 – 一個全局常量：例如，「未知」，一個新類 – 屬性均值 – 屬於同一類的所有樣本的屬性均值：更聰明 – 最可能的值：基於推理，如貝葉斯公式或決策樹 – 替換為所有可能的值（按概率加權） 清理雜訊數據 ： ● 分箱 – 首先對數據進行排序並將其劃分為等頻箱 – 然後可以通過分箱方法平滑，比如通過分箱中值平滑， 通過分箱邊界平滑等。 舉例： 價格的排序數據（以美元計）：4, 8, 9, 15, 21, 21, 24, 25, 26, 28, 29, 34 劃分為等頻（等深度）箱： – 箱 1：4、8、9、15 – 箱 2：21、21、24、25 – 箱 3：26、28、29、34 按 bin 平滑意味著： – 箱 1: 9, 9, 9, 9 – 箱 2：23、23、23、23 – 箱 3: 29, 29, 29, 29 按 bin 邊界平滑： – 箱 1: 4, 4, 4, 15 – 箱 2：21、21、25、25 – 箱 3：26、26、26、34 ● 回歸 – 通過將數據擬合到回歸函數中來平滑 ● 聚類 ● 結合電腦和人工檢查 清理不一致的數據更複雜 ● 使用依賴，比如函數依賴 ● 使用人工編譯的規則 識別或移除異常值 數據集成 多個資料庫、數據立方體或文件的集成（不介紹） 數據縮減 概念：獲得數據集的縮減表示，該表示的數量要小得多，但仍會產生相同（或幾乎相同）的分析結果 為什麼要減少數據？ 資料庫可能存儲數 TB 的數據。複雜的數據分析可能需要很長時間才能在完整的數據集上運行 維度詛咒：如果您在單位正方形中隨機選擇一個點，它與邊界距離小於 0.001 的幾率只有 0.4%，可以計算這個值在單位線段時是0.2%，單位立方體時是0.6%，在一個 1000 維的單位超立方體中，這個概率大於 99.999999%，因此高維超立方體中的大多數點都非常靠近邊界。如果您考慮足夠多的維度，那麼您認識的任何人都可能是至少一個維度的極端分子。當維數增加時，數據在它佔據的空間中變得也越來越稀疏，這樣對聚類和異常值檢測至關重要的點之間的密度和距離的定義變得沒有意義。 數據縮減策略 降維：   數據處於或接近低維子空間，用矩陣表示的話，秩就是維度 數量減少 數據壓縮 ：降維和數量減少也可以被認為是數據壓縮的形式，此外還有字元串壓縮，音影片壓縮 數據轉換 歸一化：縮放到更小的指定範圍內 – 最小-最大歸一化   – z-score 歸一化   – 十進位歸一化         屬性/特徵構建 – 從給定的屬性構造的新屬性 聚合：匯總、數據立方體構建 離散化：概念層次爬升 分箱，直方圖分析，聚類分析，決策樹分析，相關性分析 分箱（簡單離散化方法）： 等寬分箱，將範圍分成大小相等的N個區間（均勻網格） 等深度（頻率）分箱，將範圍劃分為 N 個區間，每個區間包含大約相同數量的樣本 離散區間的大小影響支援度和置信度 – 如果間隔太小,可能沒有足夠的支援 – 如果間隔太大,可能沒有足夠的置信度 可能的解決方案：使用所有可能的間隔 平滑：從數據中去除雜訊

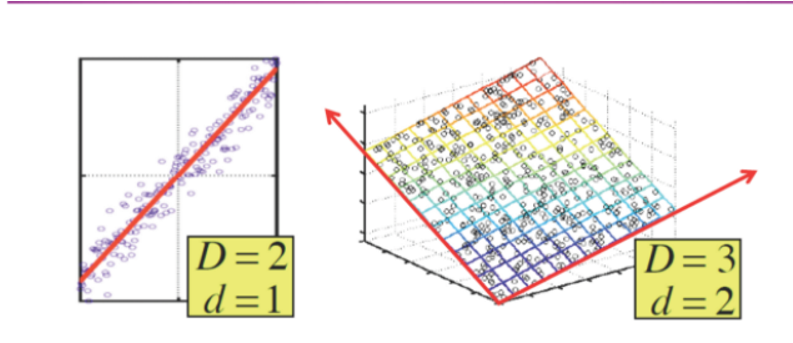
二.常見數據降維方法

（1）主成分分析

PCA的本質：

一是，要考慮去除掉特徵之間的相關性，想法是創造另一組新的特徵來描述樣本，並且新的特徵必須彼此之間不相關。

二是，在新的彼此無關的特徵集中，捨棄掉不重要的特徵，保留較少的特徵，實現數據的特徵維度降維，保持盡量少的資訊損失

一種PCA的方法：

第 1 步：將數據集圍繞原點居中

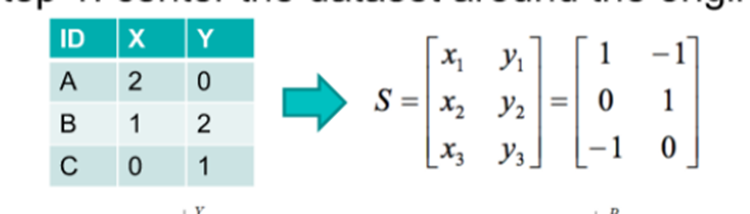
第 2 步：計算 STS

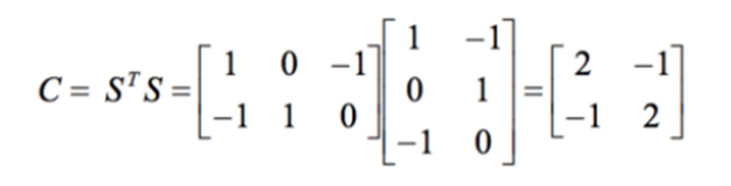
第 3 步：找到 C 的特徵值和特徵向量

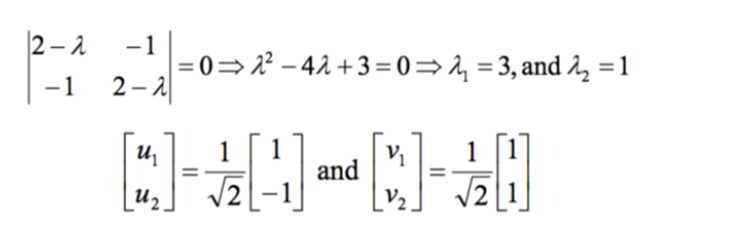
第 4 步：將數據集投影到新空間

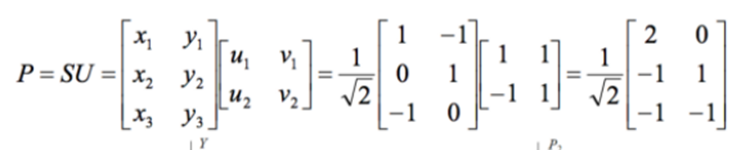
然後可以把方差最小的那個維度去掉

該演算法的解釋：（不同特徵值對應的特徵向量線性無關，對於實對稱陣是正交的）

SVD4PCA:

SVD也是對矩陣進行分解，但是和特徵分解不同，SVD並不要求要分解的矩陣為方陣。假設我們的矩陣A是一個m×n的矩陣，那麼我們定義矩陣A的SVD為：

V（右奇異向量）的列是 ATA 的特徵向量

U（左奇異向量）的列是 AAT的特徵向量

Σ的對角線上的元素（奇異值）是 ATA（或 AAT(只是相差了幾個0)）的特徵值的平方根

這裡我們用一個簡單的例子來說明矩陣是如何進行奇異值分解的。我們的矩陣A定義為：

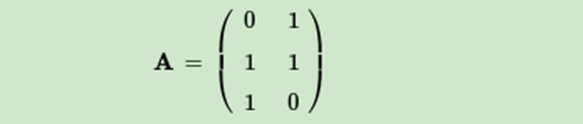
首先求出 

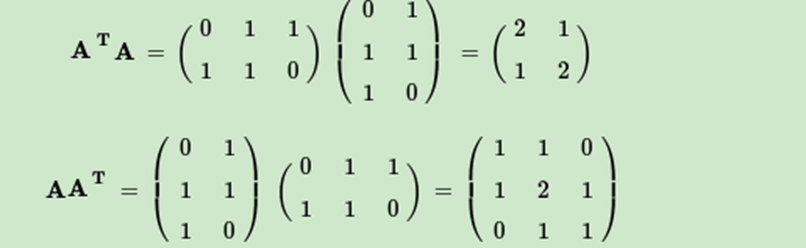
進而求出ATA的特徵值和特徵向量：

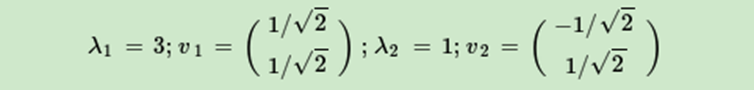
接著求出AAT的特徵值和特徵向量：

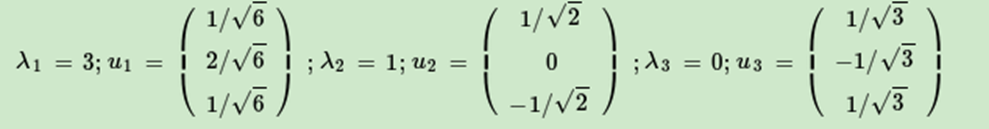
最終得到A的奇異值分解為：

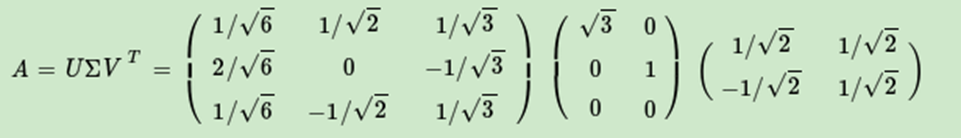
對於奇異值,它跟我們特徵分解中的特徵值類似，在奇異值矩陣中也是按照從大到小排列，而且奇異值的減少特別的快，在很多情況下，前10%甚至1%的奇異值的和就佔了全部的奇異值之和的99%以上的比例。

也就是說，我們也可以用最大的k個的奇異值和對應的左右奇異向量來近似描述矩陣。

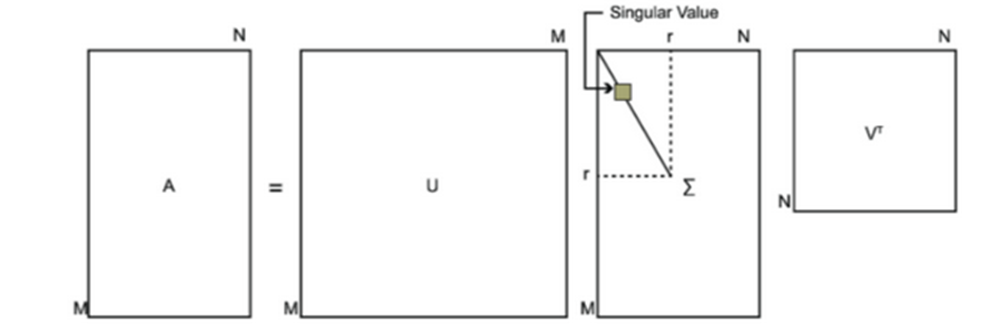
如下圖所示，現在我們的矩陣A只需要灰色的部分的三個小矩陣就可以近似描述了。

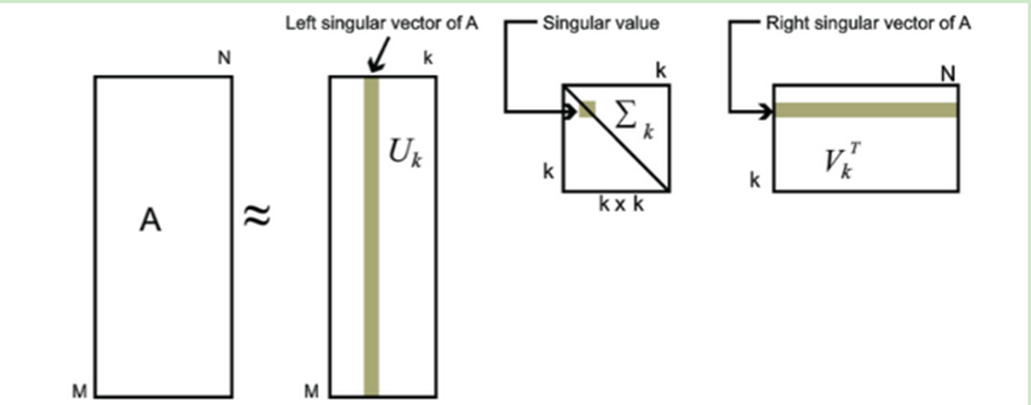
由於這個重要的性質，SVD可以用於PCA降維，來做數據壓縮和去噪。也可以用於推薦演算法，將用戶和喜好對應的矩陣做特徵分解，進而得到隱含的用戶需求來做推薦。同時也可以用於NLP中的演算法，比如潛在語義索引（LSI）。

左奇異矩陣可以用於行數的壓縮。（UΣ，即左邊兩個矩陣相乘）

右奇異矩陣可以用於列數即特徵維度的壓縮，也就是我們的PCA降維。(ΣVT，即右邊兩個矩陣相乘)

SVD作為一個很基本的演算法，在很多機器學習演算法中都有它的身影，特別是在現在的大數據時代，由於SVD可以實現並行化，因此更是大展身手，SVD的缺點是分解出的矩陣解釋性往往不強，有點黑盒子的味道，不過這不影響它的使用。

（2）屬性子集選擇

屬性消除：

冗餘屬性  – 例如，產品的購買價格和支付的銷售稅金額

不相關的屬性 – 例如，學生的 ID 通常與預測學生 GPA 的任務無關

屬性創建（特徵生成）：創建新的屬性（特徵），可以比原始屬性更有效地捕獲數據集中的重要資訊

– 屬性提取：在特定領域

– 將數據映射到新空間，例如，傅里葉變換、小波變換（未涵蓋）

– 屬性構建：組合特徵（判別頻繁模式），數據離散化

三.計算向量之間的相似性

（1）簡單匹配法和jaccard（p和q在各個屬性維度只能取0和1）

（2）餘弦相似度

二元屬性：取值為0或者1的屬性，所以也成為布爾屬性

對稱二元屬性：屬性的兩個狀態的權重相同，例如：「性別」這一屬性的取值「男性」，「女性」。

非對稱二元屬性：即狀態的權重不相同，例如：「HIV」有「陰性」和「陽性」，陽性比較稀少，更重要。

有時屬性有許多不同的類型，但需要整體相似性，使用以下方法：

可以理解為非對稱屬性上兩個向量取相同值，在相似度上應該有更小的說服力

四.計算屬性的相關性

相關不意味著因果（比如一個城市的醫院數量和汽車盜竊數量是相關的，兩者沒有直接的因果，但兩者都與第三個變數有因果關係：人口）

（1）Pearson 相關係數

衡量兩個數值屬性之間的相關性：

性質：

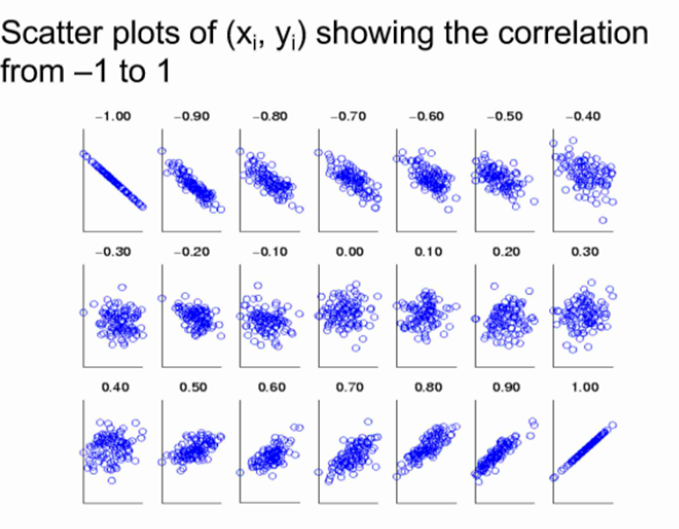
相關係數僅衡量線性相關性，它可能完全錯過非線性關係

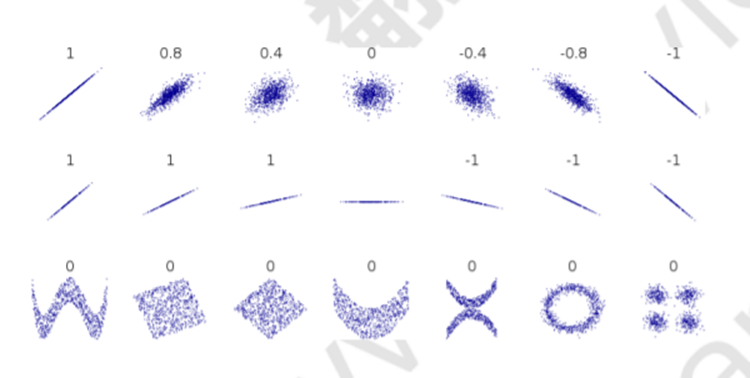
其中，相關性為1和-1時與其斜率無關

方差：

（2）卡方統計

不同於卡方檢驗，衡量兩個標稱屬性之間的相關性：

Cij是屬性x=xi且屬性y=yj的對象數量，卡方越大相關性越強，自由度(m-1)(n-1)