詳解Kalman Filter
- 2021 年 12 月 30 日
- 筆記
- Kalman Filter, 卡爾曼濾波, 演算法
中心思想
現有:
- 已知上一刻狀態,預測下一刻狀態的方法,能得到一個「預測值」。(當然這個估計值是有誤差的)
- 某種測量方法,可以測量出系統狀態的「測量值」。(當然這個測量值也是有誤差的)
我們如何去估計出系統此時真實的狀態呢?
答案是需要結合「預測值」和「測量值」。例如我們可以加權求和,但是這個權重要怎麼定義,才能準確估計出真實狀態呢?這個權重就是Kalman Filter解決的事情。
系統建模
預測方法
\]
我們假設這個預測方法是線性變換,\(B_ku_k\)是除了狀態轉移之外的控制量。\(w_k\)是預測誤差,假設為高斯分布(即均值為0的多元正態分布),其協方差矩陣為\(Q_k\)。
也就是說,下一刻我們的預測值,有一部分與上一刻狀態有關,一部分與外力控制有關(外力控制與上一刻狀態無關),還有一部分被雜訊所影響。
舉個例子:
假設一小車在x軸上向前以速度\(v\)勻速運動,\(x_k\)表示的是k時刻小車在x軸上的坐標。顯然我們有$$x_k=x_{k-1}+vt$$,這裡速度v和時間t都和上一個狀態無關,屬於讓小車位置變化的「外力」。在這個例子里\(F_kx_{k-1}\)部分就是\(x_{k-1}\),而\(B_ku_k\)部分就是\(vt\)。
測量方法
\]
因為我們不一定有測量儀器能直接測量出系統狀態,因此我們假設測量方法也是線性變換。
也就是說,當我們的測量儀器用於測量系統狀態\(x_k\)時,它的讀數是系統狀態加上一定的線性變換\(H_k\),以及測量雜訊\(v_k\),假設為高斯分布(即均值為0的多元正態分布),其協方差矩陣為\(R_k\)。
舉個例子:
我們稱體重需要得到以「斤」為單位的數據,這是系統狀態,但是我們的稱只能讀出單位為「kg」的數據(這就是\(z_k\)),那我們就需要做一個單位轉換(對應\(H_k\)),此外,由於稱不一定準,所以最後稱的讀數還得加上一點雜訊。
所有參數中:\(F_k\)、\(B_k\)、\(u_k\)、\(Q_k\)、\(H_k\)、\(R_k\)都需要已知,要麼自己根據公式和經驗定義,要麼從樣本數據里估計一個值。
演算法
Kalman Filter將一直維護對系統狀態\(x_k\)的最優估計值,以及這個估計值的偏差:
- \(\hat{x}_k\),系統狀態,可以是多維的。
- \(P_k\),\(\hat{x}_k\)的誤差。當\(\hat{x_k}\)是一維時,\(P_k\)是方差;當\(\hat{x_k}\)是多維時,\(P_k\)是協方差\(cov(\hat{x_k})\),就是\(\hat{x_k}\)里各維兩兩協方差。
預測階段
首先,通過系統的預測方法,我們可以得到「預測值」:
\]
由於誤差不知道,且假設其均值為0,所以這裡不算誤差
那麼協方差也可以從上一個狀態轉移:
\]
更新階段
這個階段需要結合「預測值」和「測量值」。先把具體的方程擺上來:
- 計算測量值殘差(innovation/measurement pre-fit residual):\(\tilde{y}_k=z_k-H_k\bar{x_k}\)(我的理解是\(H_k\)就是為了把測量值和預測值轉換到同一個空間)
- 計算測量值殘差的協方差(Innovation (or pre-fit residual) covariance):\(S_k=H_k\bar{P}_kH_k^T+R_k\)
- 計算卡爾曼增益(Kalman Gain):\(K_k=\bar{P}_kH_k^TS_k^{-1}\)
- 「更新」 最終得到的估計值:\(\hat{x}_k=\hat{x}_{k-1}+K_k\tilde{y}_k\)
- 「更新」 最終得到的估計值的協方差:\(P_k=(I-K_kH_k)P_{k-1}\)
總之最後的演算法就是,每得到一個「測量值」,就重複一遍預測和更新階段。
\(\mathbf{K}\)就是Kalman Gain,它衡量了「測量值」和「預測值」之間的權重比例,\(\mathbf{K}\)越大,「測量值」所佔權重越大。從公式可以看出:
- \(Q_k\)越大,\(\bar{P}_k\)越大,\(\mathbf{K_k}\)越大。這從物理意義上也是說得通的,當預測值的誤差更大的時候,當然應該多信任測量值。
- \(R_k\)越大,\(S_k\)越大,\(\mathbf{K_k}\)越小。也就是說,當「測量值」的誤差越大時,該公式將更信任「預測值」。
所有參數中,\(F_k\)、\(B_k\)、\(u_k\)、\(H_k\)基本都需要根據你的問題的建模來決定,而除此之外的\(Q_k\)和\(R_k\)就是兩個用於控制預測靈活性的參數,有點類似於指數滑動平均演算法的那個\(\alpha\)。
更新階段原理(試圖)詳解
結合「預測值」和「測量值」的思想



(結合高斯分布解釋)具體公式怎麼推導
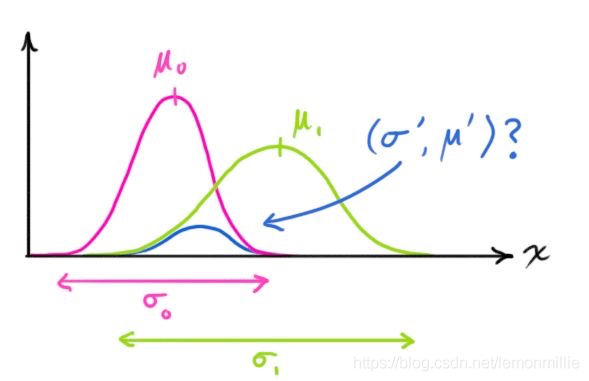
讓我們從一維看起,設方差為\(\sigma^2\),均值為\(\mu\),一個標準一維高斯鐘形曲線方程如下所示:
\]
那麼兩條高斯曲線相乘呢?
\]
把這個式子按照一維方程進行擴展,可得:
\]
\]
如果有些太複雜,我們用k簡化一下:
\]
\]
\]
以上是一維的內容,如果是多維空間,把這個式子轉成矩陣格式:
\]
\]
\]
其中,\(\Sigma\)表示協方差。
代入到Kalman Filter里,我們把「預測分布」\((\mu_0, \Sigma_0)=(H_k\bar{x}_k,H_k\bar{P}_kH_k^T)\),和「測量分布」\((\mu_1, \Sigma_1)=(z_k,R_k)\)代入到上面的等式里,那麼新分布\((\mu’,\Sigma’)=(H_k\hat{x}_k, H_kP_kH_k^T)\)為:
這裡\((\mu_0, \Sigma_0)=(H_k\bar{x}_k,H_k\bar{P}_kH_k^T)\)乘以了係數\(H_k\)是為了把\(x_k\)轉換到和\(z_k\)一個坐標系。
\]
\]
\]
等式兩邊消掉\(H_k\)並化簡後:
\]
\]
\]

