論文解讀（SDNE）《Structural Deep Network Embedding》

2021 年 12 月 6 日
筆記
論文解讀

論文題目：《Structural Deep Network Embedding》
發表時間： KDD 2016
論文作者：  Aditya Grover;Aditya Grover; Jure Leskovec
論文地址：  Download
Github：   Go1、Go2

ABSTRACT

Motivation

　　由於底層網路結構複雜，Shallow model 無法捕捉高度非線性的網路結構，導致網路表示次優。因此，如何找到一種能夠有效捕捉高度非線性網路結構並保留全局和局部結構的方法是一個開放而重要的問題。

　　Structural Deep Network Embedding method, namely SDNE. A semi-supervised deep model.

　　SDNE model has multiple layers of non-linear functions, thereby being able to capture the highly non-linear network structure.

　　Then we propose to exploit the first-order and second-order proximity jointly to preserve the network structure.

- The second-order proximity is used by the unsupervised component to capture the global network structure.
- The first-order proximity is used as the supervised information in the supervised component to preserve the local network structure.

1. Introduction

　　學習 network representations 面臨以下巨大挑戰：

High non-linearity: the underlying structure of the network is highly non-linear.
Structure-preserving: The underlying structure of the network is very complex. The similarity of vertexes is dependent on both the local and global network structure. Therefore, how to simultaneously preserve the local and global structure is a tough problem. 　　
Sparsity: Many real-world networks are often so sparse that only utilizing the very limited observed links is not enough to reach a satisfactory performance .

　　shallow models:

- IsoMAP
- Laplacian Eigenmaps (LE) 　　
- Line

　　提出 SDNE 是為保持圖結構和解決稀疏問題。

　　在 Figure 1，證明了具有 second-order proximity 的頂點對的數量比具有 first-order proximity 的頂點對的數量大得多。因此，二階鄰近度的引入能夠在表徵網路結構方面提供更多資訊。

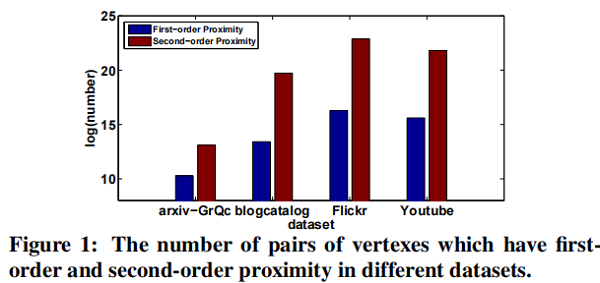
2. Related work

2.1 Deep Neural Network

　　聊聊最近相關的 Deep Neural Network，說說我們的方法和別人的不同。

- 首先，我們的工作重點是學習低維結構保留網路表示。
- 其次，考慮頂點之間的一階和二階鄰近度以保持局部和全局網路結構。

2.2 Network Embedding

　　一些早期的工作，如 $LLE$ ，$IsoMap$ 首先基於特徵向量構建親和圖，然後求解特徵向量作為NE（Network embedding）。
　　$DeepWalk$ 結合 $random walk$ 和 $skip-gram$ 來學習網路表示。儘管在經驗上是有效的，但它缺乏明確的目標函數來闡明如何保留網路結構。它傾向於只保留二階接近度。

3. Structural deep network embedding

　　在本節中，我們首先定義問題。然後我們介紹了所提出的 SDNE 的半監督深度模型。最後我們對該模型進行了一些討論和分析。

　　Definition 1. (Graph) A graph is denoted as $G = (V, E)$, where $V = {v_1, …, v_n}$ represents $n$ vertexes and $E=\left\{e_{i, j}\right\}_{i, j=1}^{n}$ represents the edges.Each edge $e_{i,j}$ is associated with a weight $s_{i,j} ≥ 0$ . For $v_i$ and $v_j$ not linked by an edge, $s_{i,j} = 0$ . Otherwise, for unweighted graph $s_{i,j} = 1$ and for weighted graph, $s_{i,j} > 0$ .

　　Definition 2. (First-Order Proximity) The first-order proximity describes the pairwise proximity between vertexes. For any pair of vertexes, if $s_{i,j} > $0, there exists positive first-order proximity between $v_i$ and $v_j$ . Otherwise, the first-order proximity between $v_i$ and $v_j$ is 0.

　　DEFINITION 3. (Second-Order Proximity) The second-order proximity between a pair of vertexes describes the proximity of the pair’s neighborhood structure. Let $\mathcal{N}_{u}=\left\{s_{u, 1}, \ldots, s_{u,|V|}\right\}$ denote the first-order proximity between $v_{u}$ and other vertexes. Then, secondorder proximity is determined by the similarity of $\mathcal{N}_{u}$ and $\mathcal{N}_{v}$ .

　　Definition 4. (Network Embedding) Given a graph denoted as $G=(V, E)$ , network embedding aims to learn a mapping function $f: v_{i} \mapsto \mathbf{y}_{\mathbf{i}} \in \mathbb{R}^{d}$ , where $d \ll|V|$ . The objective of the function is to make the similarity between $\mathbf{y}_{\mathbf{i}}$ and $\mathbf{y}_{\mathbf{j}} $ explicitly preserve the first-order and second-order proximity of $v_{i}$ and $v_{j}$ .

　　回憶：

　　上述解釋可以參考：論文解讀（LINE）《LINE: Large-scale Information Network Embedding》

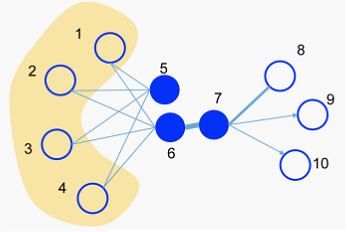
3.2 The Model

3.2.1 Framework

　　一個 semi-supervised 的深度模型，其框架如圖 Figure 2 所示.

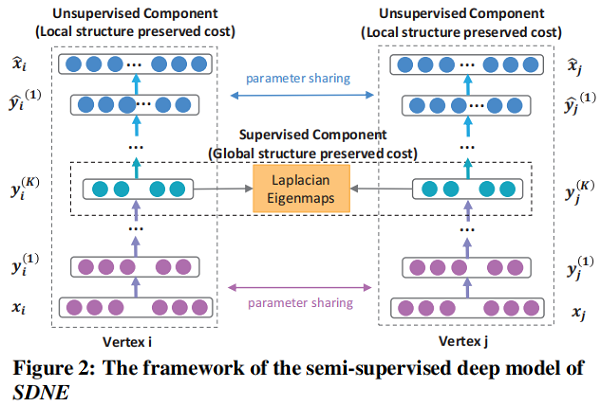
3.2.2 Loss Functions

　　我們在 Table 1 中定義了一些術語和符號，稍後將使用這些術語和符號。

　　首先回顧一下深度自編碼器的關鍵思想如下：

　　兩部分，即 Encoder 和 Decoder :

- Encoder 由多個 non-linear functions 組成，這些函數將 input data 映射到 representation space。
- Decoder 還由多個 non-linear functions 組成，將表示空間中的表示映射到 reconstruction space。

　　給定輸入 $ x_i$，每層的 hidden representations 可以表示為：

　　　　　　　　$\begin{array}{l}\mathbf{y}_{i}^{(1)}=\sigma\left(W^{(1)} \mathbf{x}_{i}+\mathbf{b}^{(1)}\right) \\\mathbf{y}_{i}^{(k)}=\sigma\left(W^{(k)} \mathbf{y}_{i}^{(k-1)}+\mathbf{b}^{(k)}\right), k=2, \ldots, K\end{array}\quad \quad \quad \quad (1)$

　　獲得 $\mathbf{y}_{i}^{(K)}$ 後 , 可以通過反轉編碼器的計算過程來獲得輸出 $\hat{\mathbf{x}}_{i}$。自編碼器的目標是最小化輸出和輸入的重構誤差。損失函數如下所示：

　　　　　　　　$\mathcal{L}=\sum \limits _{i=1}^{n}\left\|\hat{\mathbf{x}}_{i}-\mathbf{x}_{i}\right\|_{2}^{2}$

　　受 Autoencoder 的啟發，我們使用鄰接矩陣 $S$ 作為自編碼器的輸入，即 $x_i = s_i$ ，由於每個實例 $s_i$ 表徵了頂點 $v_i$ 的鄰域結構，重建過程將使具有相似鄰域結構的頂點具有相似的鄰域結構潛在表徵。

　　通過分析，我們不能直接使用 $S$ 矩陣，因為網路的稀疏性，$S$ 中非零元素的數量遠遠少於零元素的數量。如果直接使用 $S$ 作為傳統自編碼器的輸入，則更容易重構 $S$ 中的零元素，即出現很多 $0$ 元素。

　　為解決上述問題，我們對非零元素的重構誤差施加了比零元素更大的懲罰。

　　修正後的目標函數如下所示：

　　　　　　　　$\begin{aligned}\mathcal{L}_{2 n d} &=\sum \limits _{i=1}^{n}\left\|\left(\hat{\mathbf{x}}_{i}-\mathbf{x}_{i}\right) \odot \mathbf{b}_{\mathbf{i}}\right\|_{2}^{2} \\&=\|(\hat{X}-X) \odot B\|_{F}^{2}\end{aligned}\quad \quad \quad \quad (3)$

　　其中 $\odot$ 表示 Hadamard 積（對應位置相乘），$\mathbf{b}_{\mathbf{i}}=\left\{b_{i, j}\right\}_{j=1}^{n}$ 。如果 $s_{i, j}= 0, b_{i, j}=1$ ，否則 $b_{i, j}=\beta>1$ 。現在，通過使用以鄰接矩陣 $S$ 作為輸入的修改後的深度自動編碼器，具有相似鄰域結構的頂點將被映射到表示替換中的附近。 SDNE 的 Unsupervised Component 可以通過重建頂點之間的二階接近度來保留全局網路結構。

　　為捕捉局部結構，我們使用一階鄰近度來表示局部網路結構。我們設計了 supervised component 以利用一階接近度。該目標的損失函數定義如下：

　　　　　　　　$\begin{aligned}\mathcal{L}_{1 s t} &=\sum \limits _{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{i}^{(K)}-\mathbf{y}_{j}^{(K)}\right\|_{2}^{2} \\&=\sum \limits _{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|_{2}^{2}\end{aligned} \quad \quad \quad \quad (4)$

　　Eq.4 借用了 Laplacian Eigenmaps 的思想，當相似的頂點在嵌入空間中被映射到很遠的地方時，它會產生懲罰。

　　為了同時保持 first-order 和 second-order ，我們提出了一個 semi-supervised 模型，它結合了 Eq. 4 和 Eq. 3 聯合最小化以下目標函數：

　　　　　　　　$\begin{aligned}\mathcal{L}_{\text {mix }} &=\mathcal{L}_{2 n d}+\alpha \mathcal{L}_{1 s t}+\nu \mathcal{L}_{\text {reg }} \\&=\|(\hat{X}-X) \odot B\|_{F}^{2}+\alpha \sum \limits _{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|_{2}^{2}+\nu \mathcal{L}_{\text {reg }}\end{aligned}\quad \quad \quad \quad (5)$

　　其中 $\mathcal{L}_{\text {reg }}$ 是一個 $\mathcal{L}$ 2-norm 正則化項，用於防止過擬合，其定義如下：

　　　　　　　　$\mathcal{L}_{r e g}=\frac{1}{2} \sum \limits_{k=1}^{K}\left(\left\|W^{(k)}\right\|_{F}^{2}+\left\|\hat{W}^{(k)}\right\|_{F}^{2}\right)$

3.2.3 Optimization

　　為優化上述模型，目標是最小化關於 $\theta$ 的 $\mathcal{L}_{\operatorname{mix}}$ 函數。詳細地說，關鍵步驟是計算偏導數（partial derivative）$\partial \mathcal{L}_{m i x} / \partial \hat{W}^{(k)}$ 和 $ \partial \mathcal{L}_{\operatorname{mix}} / \partial W^{(k)}$ ：

　　　　　　　　$\begin{array}{l}{\large \frac{\partial \mathcal{L}_{m i x}}{\partial \hat{W}^{(k)}}=\frac{\partial \mathcal{L}_{2 n d}}{\partial \hat{W}^{(k)}}+\nu \frac{\partial \mathcal{L}_{r e g}}{\partial \hat{W}^{(k)}} \\\frac{\partial \mathcal{L}_{m i x}}{\partial W^{(k)}}=\frac{\partial \mathcal{L}_{2 n d}}{\partial W^{(k)}}+\alpha \frac{\partial \mathcal{L}_{1 s t}}{\partial W^{(k)}}+\nu \frac{\partial \mathcal{L}_{r e g}}{\partial W^{(k)}}, k=1, \ldots, K} \end{array}\quad \quad \quad \quad (6)$

　　首先來看 $\partial \mathcal{L}_{2 n d} / \partial \hat{W}^{(K)}$ ：

　　　　　　　　$ {\large \frac{\partial \mathcal{L}_{2 n d}}{\partial \hat{W}^{(K)}}=\frac{\partial \mathcal{L}_{2 n d}}{\partial \hat{X}} \cdot \frac{\partial \hat{X}}{\partial \hat{W}^{(K)}}} \quad \quad \quad \quad (7)$

　　對於第一項，根據 Eq. 3，有：

　　　　　　　　${\large \frac{\partial \mathcal{L}_{2 n d}}{\partial \hat{X}}=2(\hat{X}-X) \odot B } \quad \quad \quad \quad (8)$

　　第二項的計算 $\partial \hat{X} / \partial \hat{W}$ 可由 $\hat{X}=$ $\sigma\left(\hat{Y}^{(K-1)} \hat{W}^{(K)}+\hat{b}^{(K)}\right) $ 計算。然後 $\partial \mathcal{L}_{2 n d} / \partial \hat{W}^{(K)}$ 可以計算出。基於反向傳播，我們可以迭代地得到 $\partial \mathcal{L}_{2 n d} / \partial \hat{W}^{(k)}, k=$ $1, \ldots K-1$ 和 $\partial \mathcal{L}_{2 n d} / \partial W^{(k)}, k=1, \ldots K $ 。現在 $\mathcal{L}_{2 n d}$ 的偏導數計算完成。

　　現在計算 $\partial \mathcal{L}_{1 s t} / \partial W^{(k)}$. $\mathcal{L}_{1 s t}$ 可以表述為:

　　　　$\mathcal{L}_{1 s t}=\sum_{i, j=1}^{n} s_{i, j}\left\|\mathbf{y}_{i}-\mathbf{y}_{j}\right\|_{2}^{2}=2 \operatorname{tr}\left(Y^{T} L Y\right) \quad \quad \quad \quad (9)$
　　其中 $L=D-S, D \in \mathbb{R}^{n \times n}$ 是 diagonal matrix，$D_{i, i}=$ $\sum_{j} s_{i, j} $ 。
　　然後首先關注計算 $\partial \mathcal{L}_{1 s t} / \partial W^{(K)}$ ：

　　　　$\frac{\partial \mathcal{L}_{1 s t}}{\partial W^{(K)}}=\frac{\partial \mathcal{L}_{1 s t}}{\partial Y} \cdot \frac{\partial Y}{\partial W^{(K)}} \quad \quad \quad \quad (10)$

　　因為 $Y=\sigma\left(Y^{(K-1)} W^{(K)}+b^{(K)}\right)$, 第二項 $\partial Y / \partial W^{(K)}$ 可容易計算出。對於第一項 $\partial \mathcal{L}_{1 s t} / \partial Y$，我們有:
　　　　$\frac{\partial \mathcal{L}_{1 \text { st }}}{\partial Y}=2\left(L+L^{T}\right) \cdot Y \quad \quad \quad \quad (11)$

　　同樣地，利用反向傳播，我們可以完成對的 $\mathcal{L}_{1 s t}$ 偏導數的計算。

　　現在我們得到了這些參數的偏導數。通過對參數的初始化，可以利用 $SGD$ 對所提出的深度模型進行優化。需要注意的是，由於模型的非線性較高，在參數空間中存在許多局部最優。因此，為了找到一個良好的參數空間區域，我們首先使用 Deep Belief Network 對參數進行 pretrain ，這在文獻中被證明是深度學習的必要參數初始化。

　　SDNE 完整演算法在 Alg 1 中提出。

3.3 Analysis and Discussions

New vertexes

　　網路嵌入的一個實際問題是如何學習新到達的頂點的表示，對於一個新節點 $v_k$，如果它與現有的頂點的連接已知，我們可以得到它的鄰接向量，其中$s_{i，k}$ 表示現有的 $v_i$ 和新的頂點 $v_k$ 之間的相似性。可以簡單地將 $x$ 輸入我們的深度模型，並使用訓練後的參數 $θ$ 來得到 $v_k$ 的表示。對於不知道鄰接向量的情況，SDNE 和最新的方法都無法解決。

Training Complexity:

　　不難看出，我們的模型的訓練複雜度是 $O(ncdI)$，其中 $n$ 是頂點數，$d$ 是隱藏層的最大維數，$ c$ 是網路的平均度，$I$ 是迭代次數。

4. EXPERIMENTS

4.1 Datasets

　　 Three social networks, one citation network and one language network, for three real-world applications, i.e. multi-label classification, link prediction and visualization.　　

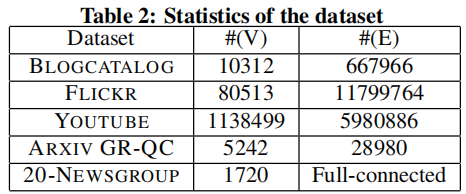
　　數據集的詳細統計數據如 Table 2 所示。

4.2 Baseline Algorithms

DeepWalk : It adopts random walk and skip-gram model to generate network representations.
LINE : It defines loss functions to preserve the first-order or second-order proximity separately. After optimizing the loss functions, it concatenates these representations.
GraRep : It extends to high-order proximity and uses the SVD to train the model. It also directly concatenates the representations of first-order and high-order.
Laplacian Eigenmaps (LE) : It generates network representations by factorizing the Laplacian matrix of the adjacency matrix. It only exploits the first-order proximity to preserve the network structure.
Common Neighbor : It only uses the number of common neighbors to measure the similarity between vertexes. It is used as the baseline only in the task of link prediction.

4.3 Evaluation Metrics

precision@k

　　　　$\operatorname{precision} @ k(i)=\frac{\left|\left\{j \mid i, j \in V, \operatorname{index}(j) \leq k, \Delta_{i}(j)=1\right\}\right|}{k}$

Mean Average Precision (MAP)

　　　　$A P(i)=\frac{\sum_{j} \text { precision } @ j(i) \cdot \Delta_{i}(j)}{\left|\left\{\Delta_{i}(j)=1\right\}\right|}$

　　　　$M A P=\frac{\sum_{i \in Q} A P(i)}{|Q|}$

Macro-F1

　　　　$\text { Macro }-F 1=\frac{\sum_{A \in \mathcal{C}} F 1(A)}{|\mathcal{C}|}$

Micro-F1

　　　　$\begin{gathered} \operatorname{Pr}=\frac{\sum_{A \in \mathcal{C}} T P(A)}{\sum_{A \in \mathcal{C}}(T P(A)+F P(A))}, R=\frac{\sum_{A \in \mathcal{C}} T P(A)}{\sum_{A \in \mathcal{C}}(T P(A)+F N(A))} \\ M i c r o-F 1=\frac{2 * P r * R}{P r+R}\end{gathered}$

4.4 Parameter Settings

　　 The dimension of each layer is listed in Table 3.
　　　　

　　更多參數設置看論文。

4.5 Experiment Results

4.5.1 Network Reconstruction

　　對於給定的一個網路，我們使用不同的網路嵌入方法來學習網路的表示，然後預測原始網路的 link。

　　precision@k 和 MAP 都可以用作度量指標。關於 precision@k 的結果如 Figure 3 所示。在 MAP 上的結果如 Table 4 所示。

4.5.2 Multi-label Classification

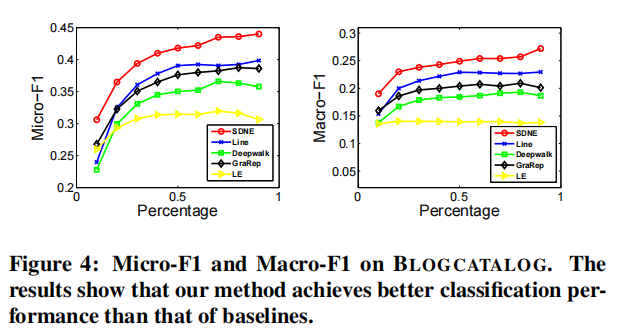
4.5.3 Link Prediction

　　在本節中，我們將專註於 link prediction task ，並進行了兩個實驗。第一種評估整體性能，第二種評估網路的不同稀疏性如何影響不同方法的性能。

　　我們隨機隱藏部分現有的鏈路，並使用網路來訓練網路嵌入模型。訓練結束後，我們可以得到每個頂點的表示，然後使用所得到的表示來預測未被觀察到的鏈接。

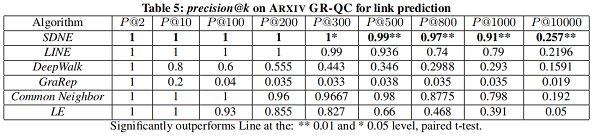
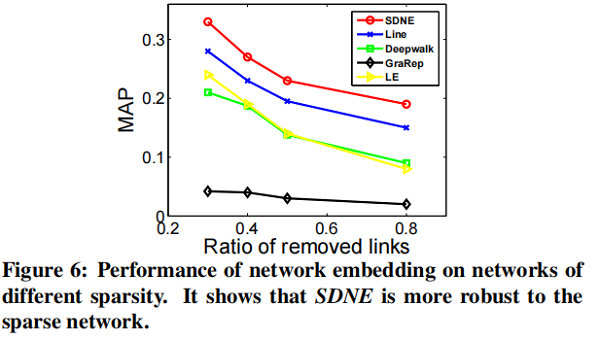
4.5.4 Visualization

4.6 Parameter Sensitivity

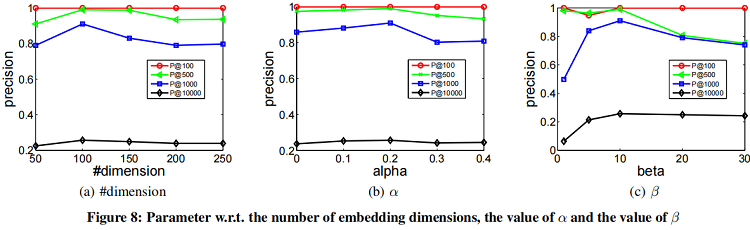
5. CONCLUSIONS

　　本文提出了一種結構深度網路嵌入編碼，即SDNE來進行網路嵌入。具體來說，為了捕獲高度非線性的網路結構，我們設計了一個具有多層非線性函數的半監督深度模型。為了進一步解決結構保持和稀疏性問題，我們共同利用一階接近性和二階接近性來表徵局部和全局網路結構。通過在半監督深度模型中聯合優化它們，學習到的表示保持了局部-全局結構，並對稀疏網路具有魯棒性。根據經驗，我們評估了在各種網路數據集和各種應用程式中生成的網路表示。結果表明，與最先進的方法相比，我們的方法取得了實質性的收益。我們未來的工作將集中於如何學習一個與現有頂點沒有鏈接的新頂點的表示。

『總結不易，加個關注唄！』

Tags: 論文解讀