對於multitaper多窗口譜估計的理解及步驟 (對應matlab中pmtm函數）譜減法相關

• 2021 年 11 月 6 日
• 筆記
• Multitaper, 多窗譜估計, 時頻訊號, 語音增強

對於多窗口譜估計的理解

0. 緣起

在語音增強通過改進的譜減法進行譜估計時，使用多窗譜估計法要優於我們一般遇到的周期法譜估計，中文相關的資料不多，這裡分享一下我學習理解到的內容。

1. PMTM 含義

• P: PSD (Power spectral density)
• MTM: Multi- Taper Method

2. 與我們常用的周期譜估計的區別

• 正常的周期法: 頻率估計是取幀，一幀加窗(一般漢寧窗)然後做頻率變換,然後將每幀的頻譜做一個平均
• 多窗譜法：頻率估計是取幀，一幀分別與多窗(一般為幾個k不一樣的slepian窗)中的每個窗相乘，然後做頻率變換, 將每個窗頻率變換的結果 相加得到最終的一幀頻譜結果

PMTM 中常用的窗函數：

• Slepian

• Sine

  

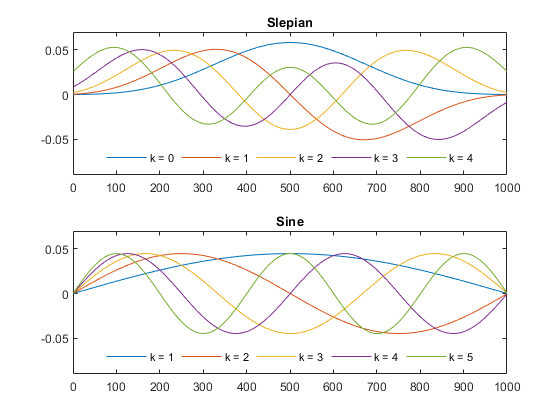
  k不同，窗口不同，他們是正交的。即 向量積為0.

3. 計算過程

• step 1: 取一幀數據，分別與窗相乘，得多幾條加窗後的數據
  

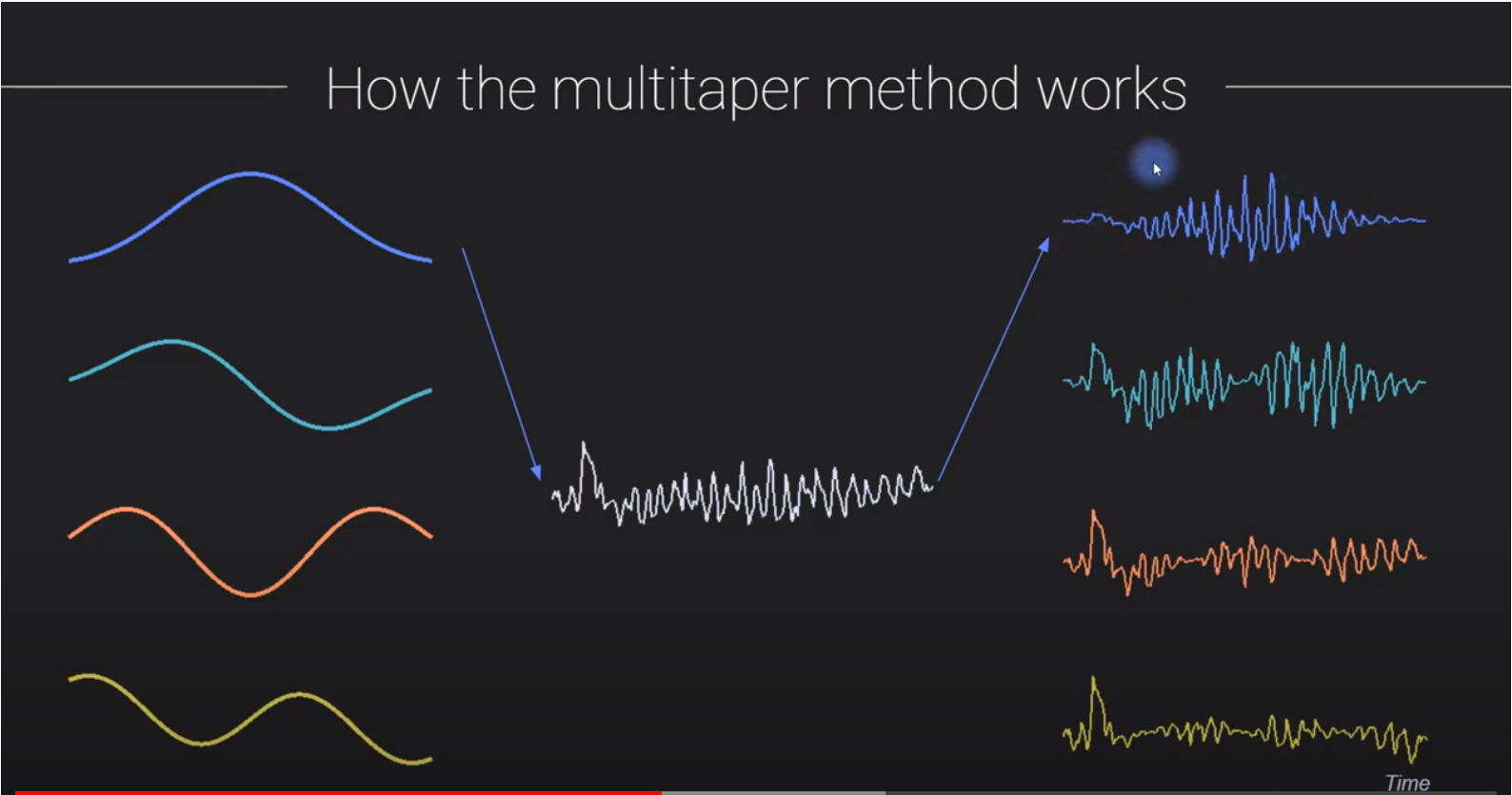
• step2: 針對每條數據（同一幀，不同加窗），進行 FFT變換

  
  

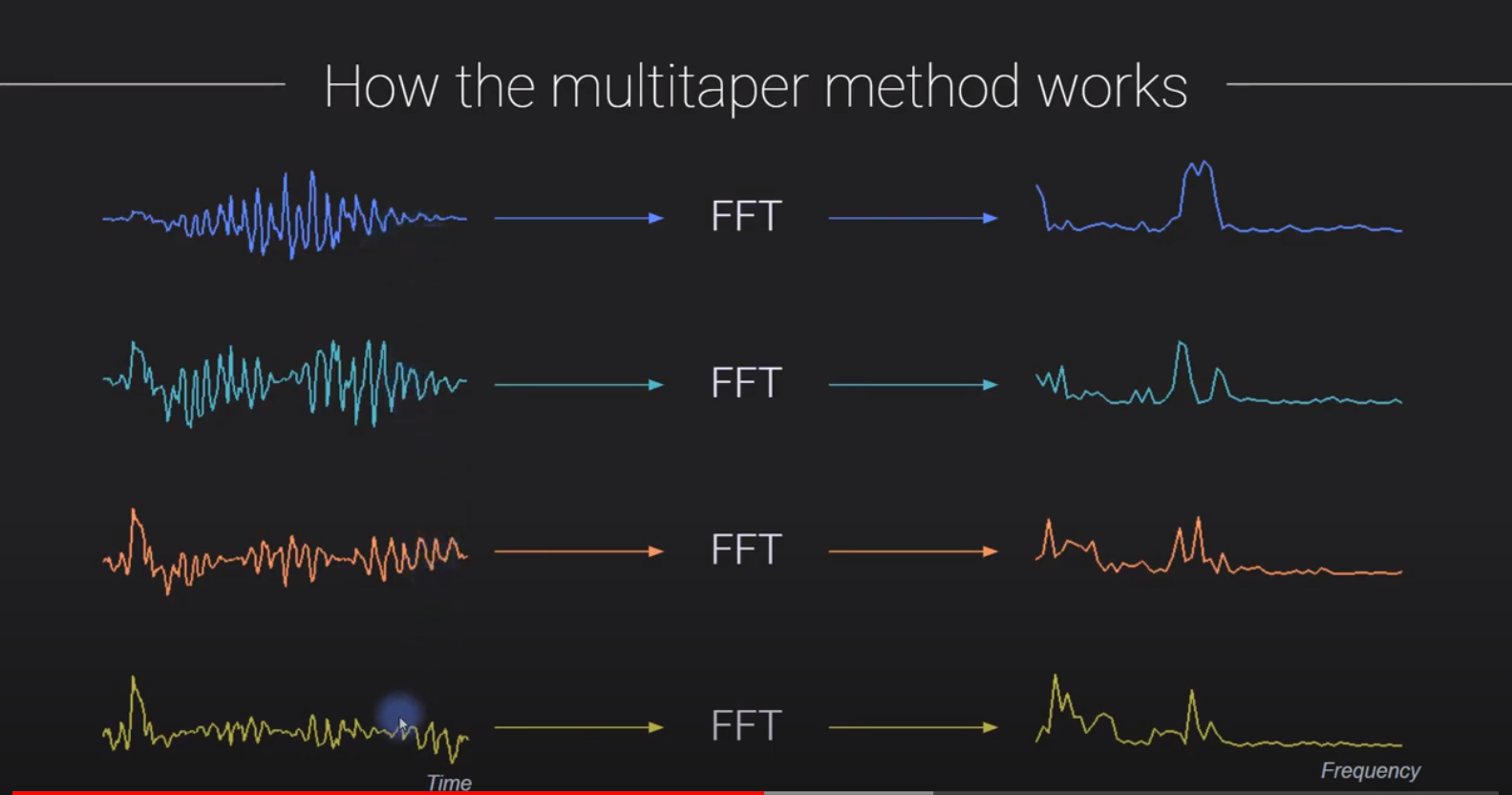
• step3: 將這幾條數據（同一幀，不同加窗）的FFT結果相加後平均，得多合成的一幀頻譜變換

  

• overview

  

5. 多窗/單窗譜估計結果對比

• 多窗譜估計得到的結果沒有一般的周期法用的單窗譜估計得到的結果那麼銳利

  

6. 程式如何生成多窗 – 以sin為例

6.1 生成正交窗的公式程式碼

N為數據的點數

figure
N = 1000;
nw = 3;
ns = 2*(nw)-1;

n = 1:N;
k = 1:ns;

sine_tprs_array = sqrt(2/(N+1))*sin(pi*n'*k/(N+1));   % 生成多窗口函數
% g_1(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*1/(1000+1))
% g_2(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*2/(1000+1))
% g_3(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))
% g_4(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))
% g_5(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))

lbs = "Sine";

% subplot(2,1,kj)
for kj= 1:5
    subplot(5,1,kj)
    plot(sine_tprs_array(:,kj))
    title(lbs)
    legend(append('k = ',string(kj)), ...
        'Orientation','horizontal','Location','south')
    legend('boxoff')
    ylim([-0.09 0.07])
end

6.2 計算是否符合正交

sine_tprs_array = tprs(:,:,2);
rslt = zeros([5,5]);
for i =1:5
    for j = 1:5
        rslt(i,j) = sine_tprs_array(:,i)'*sine_tprs_array(:,j); % 計算向量積，檢查是否正交
    end   
end`



>> rslt

rslt =

    1.0000    0.0000   -0.0000   -0.0000    0.0000
    0.0000    1.0000   -0.0000    0.0000   -0.0000
   -0.0000   -0.0000    1.0000   -0.0000   -0.0000
   -0.0000    0.0000   -0.0000    1.0000   -0.0000
    0.0000   -0.0000   -0.0000   -0.0000    1.0000
% 可見這幾個窗函數都是正交的。

7. Reference

1. Multitaper power spectral density estimate – MATLAB pmtm
2. 頻譜分析中如何理解taper？ – 知乎
3. [數字訊號中功率譜估計相關方法簡介及MATLAB實現_matlab功率譜
4. The multi-taper method – YouTube