決策樹 機器學習,西瓜書p80 表4.2 使用資訊增益生成決策樹及後剪枝
使用資訊增益構造決策樹,完成後剪枝
1 構造決策樹
1 根結點的選擇
色澤 資訊增益
根據色澤劃分為 青綠,烏黑,淺白 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^2) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,色澤)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{4}{10}\times 1+\frac{4}{10} \times 0.811+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
根蒂 資訊增益
根據根蒂劃分為 蜷縮 稍蜷 硬挺 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{5} log_2 \frac{2}{5}+\frac{3}{5} log_2 \frac{3}{5})=0.971 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{5}{10}\times 0.971+\frac{4}{10} \times 1+\frac{1}{10}\times0) \\
&= 0.1145\end{aligned}
\]
敲聲 資訊增益
根據色澤劃分為 濁響,沉悶,清脆 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,敲聲)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&=0.2346\end{aligned}
\]
紋理 資訊增益
根據 紋理 劃分為 清晰 稍糊 模糊 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,紋理)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&= 0.2346\end{aligned}
\]
臍部 資訊增益
根據色澤劃分為 凹陷,稍凹,平坦 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,臍部)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{4}{10}\times 0.811+\frac{4}{10} \times 1+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
觸感 資訊增益
根據色澤劃分為 硬滑,軟粘 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{3}{6} log_2 \frac{3}{6}+\frac{3}{6} log_2 \frac{3}{6})=1 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,觸感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{6}{10}\times 1 +\frac{4}{10} \times 1 \\
&= 0\end{aligned}
\]
選擇根結點構建決策樹
\[\begin{aligned}
Gain(D,色澤)=0.2756 \ Gain(D,根蒂)=0.1145 \ Gain(D,敲聲)=0.2346 \\
Gain(D,紋理)=0.2346 \ Gain(D,臍部)=0.2756 \ Gain(D,觸感)=0\end{aligned}
\]
比較六個屬性的資訊增益大小,選擇臍部作為根結點
則數據集被劃分為
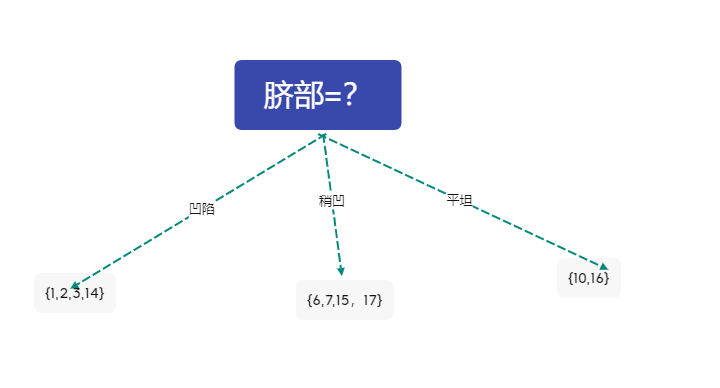
2 對分支結點\({1,2,3,14}\)進行劃分
色澤 資訊增益
根據色澤劃分為 青綠,烏黑,淺白 三個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,色澤)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 – (\frac{1}{4}\times 0+\frac{2}{4} \times 0 +\frac{1}{4}\times 0) \\
&= 0.811\end{aligned}
\]
根蒂 資訊增益
根據根蒂劃分為 蜷縮 稍蜷 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 – (\frac{3}{4}\times 0 +\frac{1}{4} \times 0) \\
&= 0.811\end{aligned}
\]
敲聲 資訊增益
根據色澤劃分為 濁響,沉悶 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,敲聲)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 – (\frac{2}{4}\times 0 +\frac{2}{4} \times 1 ) \\
&=0.311\end{aligned}
\]
紋理 資訊增益
根據 紋理 劃分為 清晰 稍糊 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,紋理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 – (\frac{3}{4}\times 0+\frac{1}{4} \times 0 ) \\
&= 0.811\end{aligned}
\]
觸感 資訊增益
根據觸感劃分為 硬滑 一個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811 \\
Gani(D,觸感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 – (\frac{4}{4}\times 0.811 ) \\
&= 0\end{aligned}
\]
選擇分類結點構建決策樹
\[\begin{aligned}
Gain(D,色澤)=0.811 \ Gain(D,根蒂)=0.811 \ Gain(D,敲聲)=0.311 \\
Gain(D,紋理)=0.811 \ \ \ Gain(D,觸感)=0\end{aligned}
\]
不妨選擇色澤作為分類依據
形成的決策樹
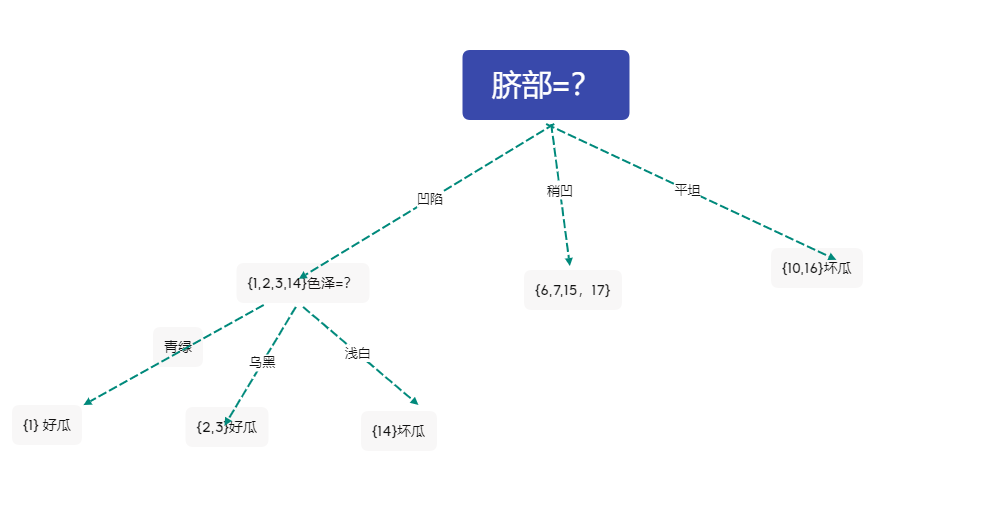
3 對分支 \({6,7,15,17}\)進行劃分
色澤 資訊增益
根據色澤劃分為 青綠,烏黑 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{0}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1 \\
Gani(D,色澤)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
根蒂 資訊增益
根據根蒂劃分為 蜷縮 稍蜷 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0。918\\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0) \\
&= 0.3115\end{aligned}
\]
敲聲 資訊增益
根據色澤劃分為 濁響,沉悶 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})= 0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,敲聲)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0 ) \\
&=0.3115\end{aligned}
\]
紋理 資訊增益
根據 紋理 劃分為 清晰 稍糊 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,紋理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
觸感 資訊增益
根據觸感劃分為 硬滑,軟粘 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,觸感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{3}{4}\times 0.918+\frac{1}{4} \times 0 ) \\
&= 0.2295\end{aligned}
\]
選擇分類結點構建決策樹
\[\begin{aligned}
Gain(D,色澤)=0 \ Gain(D,根蒂)=0.3115 \ Gain(D,敲聲)=0.3115 \\
Gain(D,紋理)=0 \ \ \ Gain(D,觸感)=0.2295\end{aligned}
\]
不妨選擇根蒂作為分類依據
此時決策樹為
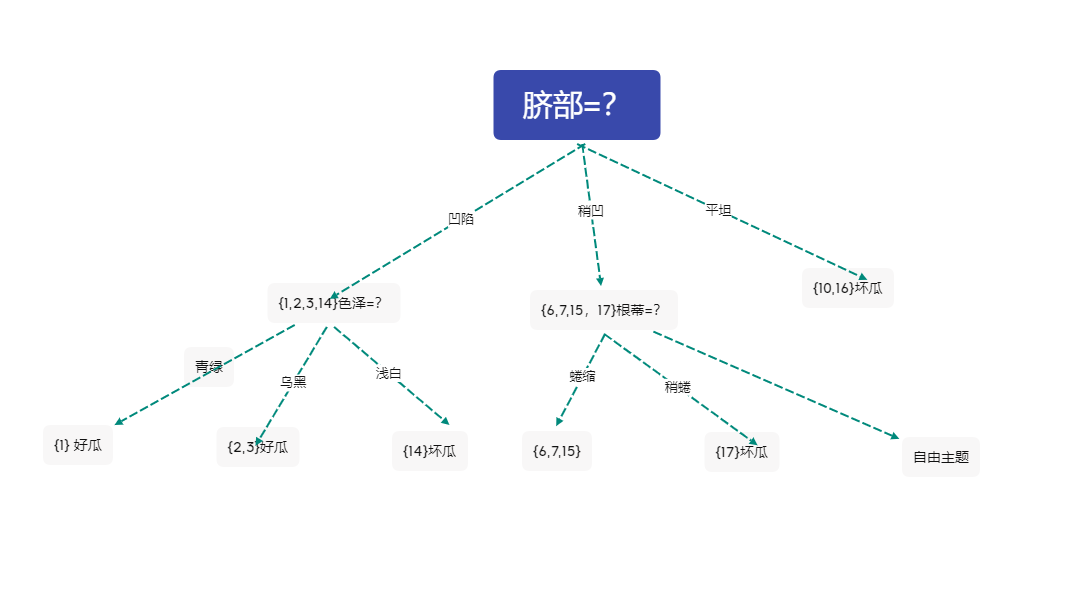
4 對分支\({6,7,15}\)進行劃分
色澤 資訊增益
根據色澤劃分為 青綠,烏黑 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})= 0.918 \\
Gani(D,色澤)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 – (\frac{1}{3}\times 0+\frac{2}{3} \times 1 ) \\
&= 0.252\end{aligned}
\]
敲聲 資訊增益
根據色澤劃分為 濁響 一個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,敲聲)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 – (\frac{3}{3}\times 0.918 ) \\
&=0\end{aligned}
\]
紋理 資訊增益
根據 紋理 劃分為 清晰 稍糊 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0\\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,紋理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 – (\frac{2}{3}\times 1+\frac{1}{3} \times 0 ) \\
&= 0.252\end{aligned}
\]
觸感 資訊增益
根據觸感劃分為 軟粘 一個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918\\
Gani(D,觸感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 – (\frac{3}{3}\times 0.918 ) \\
&= 0\end{aligned}
\]
選擇分類結點構建決策樹
\[\begin{aligned}
Gain(D,色澤)=0 .252 \ \ Gain(D,敲聲)=0 \\
Gain(D,紋理)=0.252 \ \ \ Gain(D,觸感)=0\end{aligned}
\]
不妨選擇色澤作為分類依據
此時決策樹為
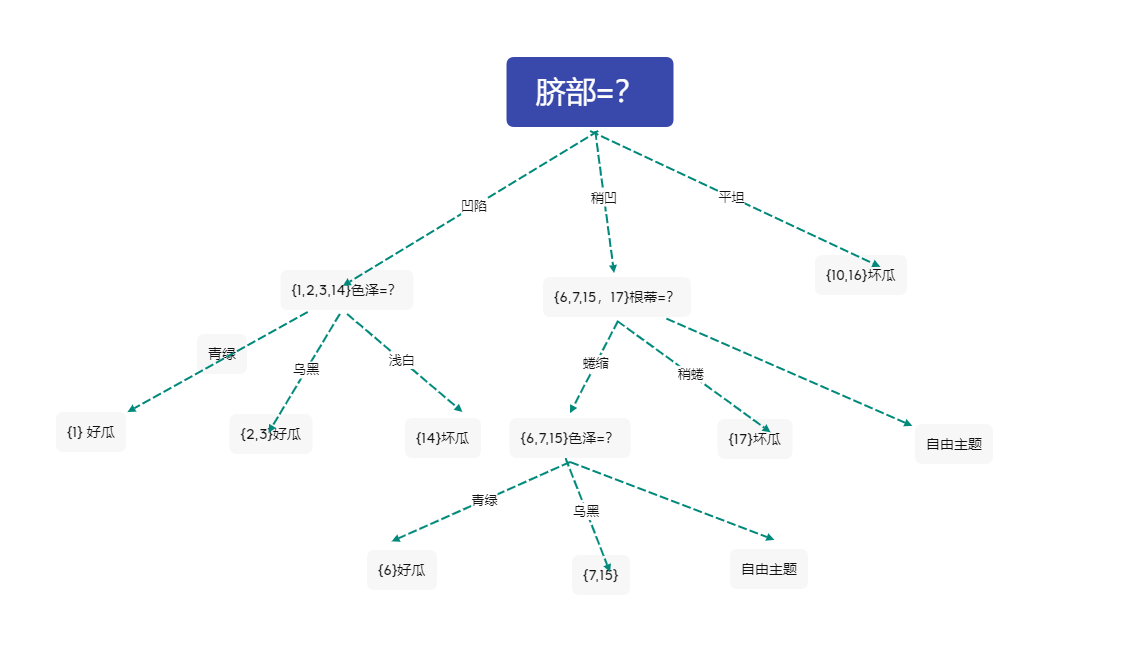
5 對分支\({7,15}\)進行劃分
敲聲 資訊增益
根據色澤劃分為 濁響 一個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,敲聲)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
紋理 資訊增益
根據 紋理 劃分為 清晰 稍糊 兩個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0\\Ent(D)&= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Gani(D,紋理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{1}{2}\times 0+\frac{1}{2} \times 0 ) \\
&= 1\end{aligned}
\]
觸感 資訊增益
根據觸感劃分為 軟粘 一個子集
計算資訊熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,觸感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 – (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
選擇分類結點構建決策樹
\[\begin{aligned}
\ \ Gain(D,敲聲)=0 \ Gain(D,紋理)=1 \ \ \ Gain(D,觸感)=0\end{aligned}
\]
選擇紋理作為分類依據
此時決策樹為
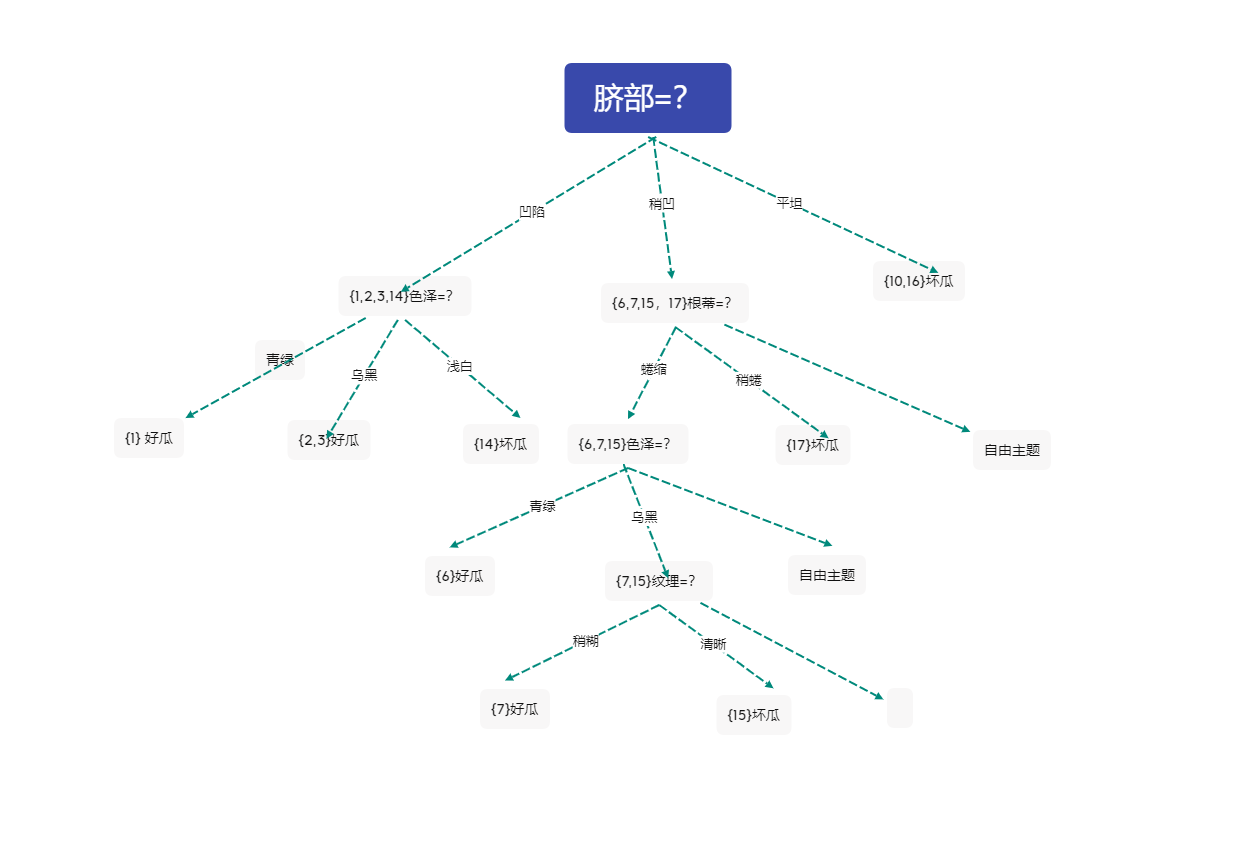
2 決策樹後剪枝
1 考慮結點\(7,15\)
原分支(剪枝前),有三個樣本被正確分類 驗證集精度為 42.8%
剪枝後的決策樹
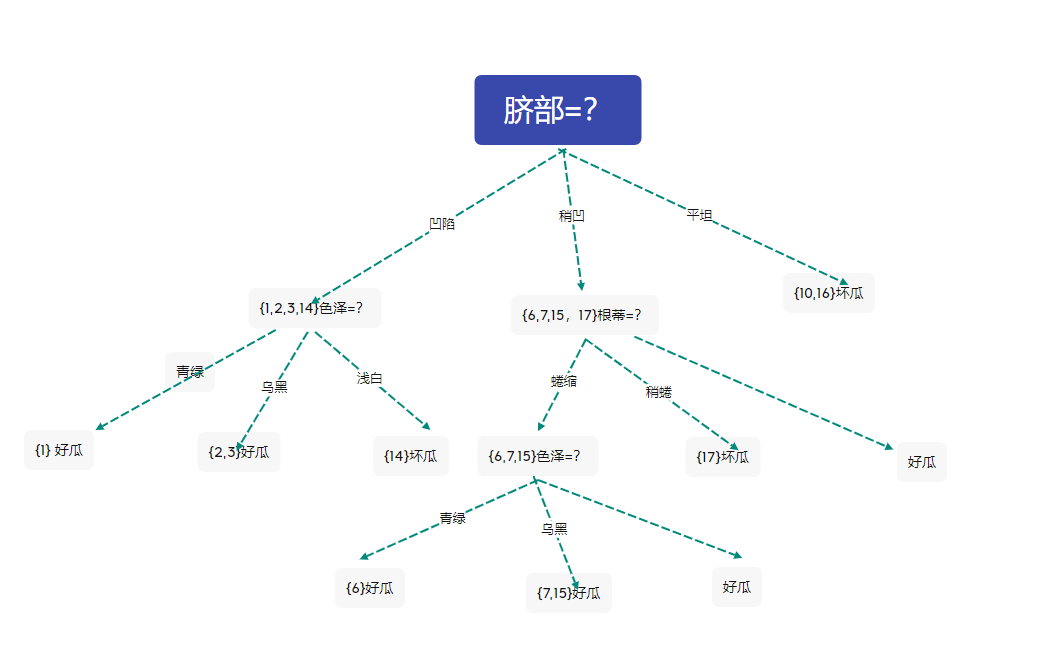
此時驗證集有四個樣本被正確分類,精度為57.1%
於是後剪枝策略決定剪枝,得到上圖的決策樹
2 考慮結點\(6,715\)色澤=?
由上圖,決策樹精度為57.1%
剪去結點後的決策樹為
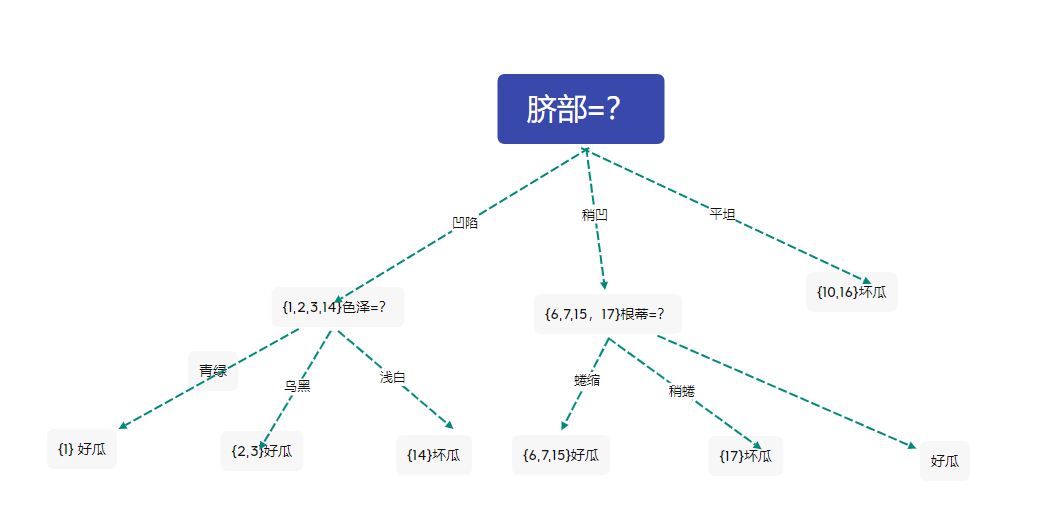
此時驗證集有四個樣本被正確分類,精度為57.1%
與未剪枝時的精度相同,西瓜書中採用了不剪枝的策略。在這裡我們不妨採用剪枝的策略,於是得到上圖的決策樹
3 考慮結點\(1,2,3,14\)色澤=?
在上圖基礎上來考慮剪去結點\(1,2,3,14\)色澤=? ,剪枝後的決策樹為
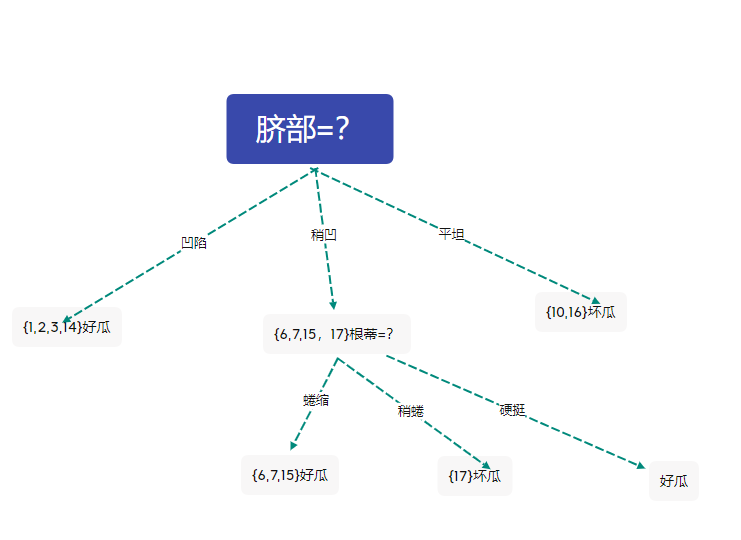
此時的決策樹正確分類的樣本5個,精度為71.4%
根據後剪枝策略,進行剪枝,得到上圖的決策樹
4考慮 \(6,7,15,17\)根蒂=?
剪枝後的決策樹為
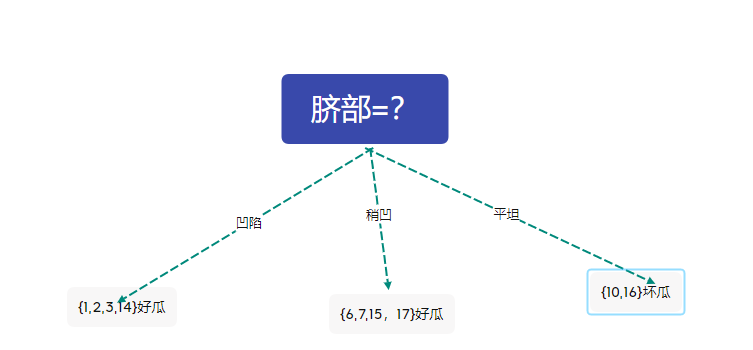
此時的決策樹的精度仍然為71.4%
與未剪枝時的精度相同,西瓜書中採用了不剪枝的策略。在這裡我們不妨採用剪枝的策略,於是得到上圖的決策樹
最終得到上圖的決策樹

