數據結構與演算法——迪傑斯特拉(Dijkstra)演算法
tip:這個演算法真的很難講解,有些地方只能意會了,多思考多看幾遍還是可以弄懂的。
應用場景-最短路徑問題
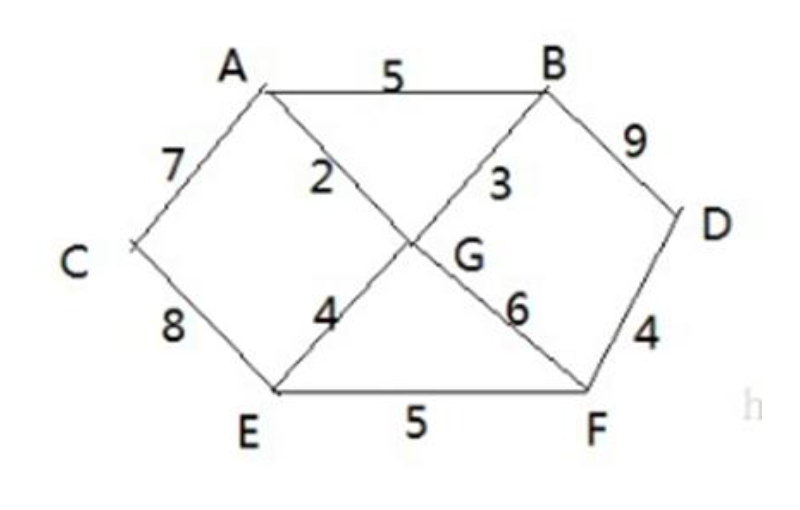
戰爭時期,勝利鄉有 7 個村莊 (A, B, C, D, E, F, G) ,現在有六個郵差,從 G 點出發,需要分別把郵件分別送到 A, B, C , D, E, F 六個村莊,各個村莊的距離用邊線表示(權) ,比如 A – B 距離 5公里
問:如何計算出 G 村莊到 其它各個村莊的 最短距離? 如果從其它點出發到各個點的最短距離又是多少?
迪傑斯特拉演算法介紹
迪傑斯特拉(Dijkstra)演算法是 典型 最短路徑演算法,用於 計算一個節點到其他節點的最短路徑。 它的主要特點是 以起始點為中心向外層層擴展(廣度優先搜索思想),直到擴展到終點為止。
迪傑斯特拉演算法過程
設:
-
v:出發頂點
-
V:為頂點集合
V{v1,v2,vi...} -
vs:已經訪問過的頂點
- 0 :未訪問
- 1:已訪問
-
dis:v 到 V 中各個頂點的距離
dis{d1,d2,di...}到自身(v 到 v)的距離為 0,v 到 Vi 的距離為 di
那麼有如下規則:
- 從 dis 中選擇值最小的 di 並移除 dis 集合,同時移除 V 集合中對應的頂點 vi,此時的 v 到 vi 即為最短路徑
- 更新 dis 集合,更新規則為:比較 v 到 V 集合中頂點的距離,與 v 通過 Vi 到 V 集合中頂點的距離值,保留較小的一個(同時也應該更新頂點的 前驅節點 為 Vi,表名是通過 Vi 達到的。)
- 重複執行兩步驟,直到最短路徑頂點為目標頂點即可結束
上面的演算法過程脫離了具體的實現,很抽象,下面通過具體一點的實現步驟過程來看看到底是怎麼弄的
迪傑斯特拉演算法-步驟

需要以下三個重要的數組:
-
already_arr:記錄各個頂點是否訪問過1 表示訪問過,0 表示未訪問過,每搜索一層(廣度優先),都會被動態更新。
比如從 G 點出發,訪問過
G,A,此時 A 不算訪問過,G 算被訪問的節點,因為要計算 G 到 A 的距離,但是 A 不是 訪問節點 或 出發節點 -
pre_visited_arr:每個下標對應的值為前一個頂點下標(前驅節點),統一動態更新比如:從 G 點出發,會訪問
G,A、G,B、G,E、G,F,那麼 A、B、E、F 的前驅節點就是 G -
dis_arr:記錄出發點到其他所有頂點的距離比如:從 G 出發,到過了
G,A,再從A,C到 C,則記錄的是 G 到 C 的路徑距離
過程如下:
-
以 G 為起點,的各個數組的初始狀態
對應的村莊 [A, B, C, D, E, F, G] 下標 [0, 1, 2, 3, 4, 5, 6] already_arr = [0, 0, 0, 0, 0, 0, 1] pre_visited_arr = [N, N, N, N, N, N, 0] dis_arr = [0, 0, 0, 0, 0, 0, 0]含義:
already_arr[n] = 0:則表示,該點還沒有訪問過already_arr[6] = 1:該點已經訪問過,因為從 G 出發,那麼 G 點自己就被訪問過了dis_arr中都為 0,因為從 G 點開始,還沒有到達過其他點pre_visited_arr[n] = N:其中 N 為一個較大的值,表示不能直接連接通的權值
-
計算過從 G 點能到達的點
A,B,E,F之後的情況如下對應的村莊 [A, B, C, D, E, F, G] 下標 [0, 1, 2, 3, 4, 5, 6 already_arr = [0, 0, 0, 0, 0, 0, 1] pre_visited_arr = [6, 6, N, N, 6, 6, 0] dis_arr = [2, 3, 0, 0, 4, 6, 0]含義:
already_arr[6] = 1:表示 G 點被訪問過pre_visited_arr[0]=6:表示 節點 A 的前驅節點是 6,即 Gdis_arr[0]:表示 G 到 A 的距離是 2
-
根據廣度優先原則(並不是以 GA,GB A 在前面而選擇 A,這裡的廣度優先指的是:以 G 為起點,那麼則把與 G 直連的全部計算,這樣一層一層的計算),會先判定 A 點是否需要作為 訪問頂點(注意不是出發頂點),需要滿足以下條件:
-
A 點沒有被訪問過
-
並且 G 點到 A 點的距離,要小於 dis_arr 中對應 G 到 A 的距離,因為可能出現以下情況:
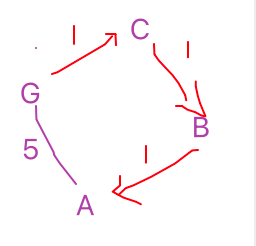
有可能其他通過其他節點到達 A 點的距離是最短的。
那麼此輪會計算
A,B、A,C,訪問之後的情況如下對應的村莊 [A, B, C, D, E, F, G] 下標 [0, 1, 2, 3, 4, 5, 6] already_arr = [1, 0, 0, 0, 0, 0, 1] pre_visited_arr = [6, 0, 0, N, 6, 6, 0] dis_arr = [2, 7, 9, 0, 4, 6, 0] 此次變動的有 ↑ ↑already_arr[0] = 1: 表示當前訪問的是 Adis_arr[1] = 7: 表示 G 到 B (中間經過 A)的距離是 7dis_arr[2] = 9: 表示 G 到 C (中間經過 A)的距離是 9
這裡就出現一個問題:

如上圖:
GAB = 7,但是GB=3,並且在訪問 G 點的時候,已經計算出了GB的距離,所以這裡GAB > GB的,它不應該被更新到這裡來。最終調節之後的結果為:對應的村莊 [A, B, C, D, E, F, G] 下標 [0, 1, 2, 3, 4, 5, 6] already_arr = [1, 0, 0, 0, 0, 0, 1] pre_visited_arr = [6, 6, 0, N, 6, 6, 0] dis_arr = [2, 3, 9, 0, 4, 6, 0] -
如果還不懂,就結合下面的程式碼進行理解。
程式碼實現
構建無向圖
老規矩,這種圖結構,都需要先構建出它的圖結構,這裡還是使用之前學過的 鄰接矩陣 構建
/**
* 迪傑斯特拉演算法-最短路徑問題
*/
public class DijkstraAlgorithm {
// 不連通的默認值
int N = 100000;
/**
* 圖:首先需要有一個帶權的連通無向圖
*/
class MGraph {
int vertex; // 頂點個數
int[][] weights; // 鄰接矩陣
char[] datas; // 村莊數據
int edgeNum; // 共有多少條邊
/**
* @param vertex 村莊數量, 會按照數量,按順序生成村莊,如 A、B、C...
* @param weights 需要你自己定義好那些點是連通的,那些不是連通的
*/
public MGraph(int vertex, int[][] weights) {
this.vertex = vertex;
this.weights = weights;
this.datas = new char[vertex];
for (int i = 0; i < vertex; i++) {
// 大寫字母 A 從 65 開始
datas[i] = (char) (65 + i);
}
// 計算有多少條邊
for (int i = 0; i < weights.length; i++) {
/*
A B C D E F G
A 0 12 100000 100000 100000 16 14
B 12 0 10 100000 100000 7 100000
j = i + 1:比如:
i=0,j=1, 那麼就是 A,B 從而跳過了 A,A
i=1,j=2, 那麼就是 B,C 從而跳過了 B,A B,B
那麼含義就出來了:跳過雙向邊的統計,也跳過自己對自己值得為 0 的統計
*/
for (int j = i + 1; j < weights.length; j++) {
if (weights[i][j] != N) {
edgeNum++;
}
}
}
}
public void show() {
System.out.printf("%-8s", " ");
for (char vertex : datas) {
// 控制字元串輸出長度:少於 8 位的,右側用空格補位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", datas[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
}
@Test
public void mGraphTest() {
int[][] weights = new int[][]{
// A B C D E F G
/*A*/ {N, 5, 7, N, N, N, 2},
/*B*/ {5, N, N, 9, N, N, 3},
/*C*/ {7, N, N, N, 8, N, N},
/*D*/ {N, 9, N, N, N, 4, N},
/*E*/ {N, N, 8, N, N, 5, 4},
/*F*/ {N, N, N, 4, 5, N, 6},
/*G*/ {2, 3, N, N, 4, 6, N}
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
System.out.printf("共有 %d 條邊\n", mGraph.edgeNum);
}
}
測試輸出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
共有 10 條邊
迪傑斯特拉演算法求解
@Test
public void dijkstraTest() {
int[][] weights = new int[][]{
// A B C D E F G
/*A*/ {N, 5, 7, N, N, N, 2},
/*B*/ {5, N, N, 9, N, N, 3},
/*C*/ {7, N, N, N, 8, N, N},
/*D*/ {N, 9, N, N, N, 4, N},
/*E*/ {N, N, 8, N, N, 5, 4},
/*F*/ {N, N, N, 4, 5, N, 6},
/*G*/ {2, 3, N, N, 4, 6, N}
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
System.out.printf("共有 %d 條邊 \n", mGraph.edgeNum);
dijkstra(mGraph, 'G');
}
// 記錄各個頂點是否訪問過
private boolean[] already_arr;
// 記錄每個下標對應的值為前一個頂點下標(前驅節點)
private int[] pre_visited_arr;
// 記錄出發點到其他所有頂點的距離
private int[] dis_arr;
private MGraph mGraph;
private void dijkstra(MGraph mGraph, char start) {
this.mGraph = mGraph;
// 三個數組的長度為 頂點的個數
already_arr = new boolean[mGraph.vertex];
pre_visited_arr = new int[mGraph.vertex];
dis_arr = new int[mGraph.vertex];
// 找到開始節點的下標
int v = 0;
for (int i = 0; i < mGraph.datas.length; i++) {
if (mGraph.datas[i] == start) {
v = i;
break;
}
}
// 初始化所有前驅節點為默認狀態,使用不可連通的 N 值表示
Arrays.fill(pre_visited_arr, N);
// 標記開始節點為訪問狀態
already_arr[v] = true;
//我們使用 N 表示沒有前驅節點
// v 是開始節點,那麼它就沒有前驅節點
pre_visited_arr[v] = N;
// 初始化從起點到到所有點的距離為最大值,後續方便通過它來與新路徑距離比較
Arrays.fill(dis_arr, N);
// 初始化,當前訪問節點的距離為 0
dis_arr[v] = 0;
// 準備工作完成:開始查找最短路徑
// 廣度優先策略:從起始節點計算它能直達的點的所有距離
update(v);
// 一共只需要計算 6 層: 7 個站點 -1
for (char data : mGraph.datas) {
// 尋找下一個訪問節點
int index = findNext();
// 標記該節點被訪問過,然後再計算與它直連點的路徑
already_arr[index] = true;
// 並繼續計算路徑
update(index);
}
// 所有節點都訪問過之後:dis_arr 中就保留了從起點 到各個點的最短距離
System.out.println(Arrays.toString(already_arr));
System.out.println(Arrays.toString(pre_visited_arr));
System.out.println(Arrays.toString(dis_arr));
System.out.println("從 " + start + " 到以下點的最短距離為:");
// 為了結果好認一點,格式化最後的結果
for (int i = 0; i < dis_arr.length; i++) {
System.out.printf("%S(%d) ", mGraph.datas[i], dis_arr[i]);
}
System.out.println();
}
/**
* 計算起點到:當前節點所有能直連的節點的距離
*
* @param v
*/
private void update(int v) {
int[][] weights = mGraph.weights; // 我們的鄰接矩陣圖
int len = 0;
// weights[v]:由於是廣度優先,所以每次只計算與該點能直連的點,也就是該點所在的一行
for (int i = 0; i < weights[v].length; i++) {
if (weights[v][i] == N) { // 不能直連,跳過
continue;
}
// 計算從起點到當前要連通節點的距離 = 起點到當前訪問節點的距離 + 訪問節點到直連節點的距離
len = dis_arr[v] + weights[v][i];
// 首先:起點G -> A, A 要沒有被訪問過
// 其次:如果當前計算新的路徑距離 小於 已經存在的 從 起點 G -> 當前計算點的距離
// 說明之前可能從其他途徑到達了 i 點,這個距離是比現在找到的距離遠
// 當前的近,那麼就更新數組中的數據
if (!already_arr[i] && len < dis_arr[i]) {
dis_arr[i] = len;
pre_visited_arr[i] = v; // 更改前驅節點,表示 經過了 v 這個點(當前正在訪問的點),到達的 i 點
}
}
}
/**
* 廣度優先策略一層計算完成之後,尋找下一個節點再計算
*
* @return
*/
private int findNext() {
int min = N, index = 0;
for (int i = 0; i < already_arr.length; i++) {
// 該節點沒有被訪問過
// 並且:從起點到達該節點的距離是最小的
// 如果是第一層執行完成之後:那麼有值的則只有:與起點能直連的那幾個
// 這裡就類似與:原來廣度優先中使用隊列來保存搜索路徑了
if (!already_arr[i] && dis_arr[i] < min) {
min = dis_arr[i];
index = i;
}
}
return index;
}
測試輸出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
共有 10 條邊
[true, true, true, true, true, true, true]
[6, 6, 0, 5, 6, 6, 100000]
[2, 3, 9, 10, 4, 6, 0]
從 G 到以下點的最短距離為:
A(2) B(3) C(9) D(10) E(4) F(6) G(0)
從輸出結果可以看到:
-
[true, true, true, true, true, true, true]所有節點都訪問過了
-
[6, 6, 0, 5, 6, 6, 100000]從起點到達每個節點的前驅節點如數組上所示

- G 到 A:前驅就是 G,表示從 G 到達的 A
- G 到 B:前驅也是 G
- G 到 C:前驅是 A,表示從 G 到 C,至少經過了 A,這裡看就是 GAC
- …
- G 到 G:這裡用了最大值表示,是他自己
-
[2, 3, 9, 10, 4, 6, 0]即A(2) B(3) C(9) D(10) E(4) F(6) G(0)-
從 G 到 A 最短路徑為 2
-
從 G 到 B 最短路徑為 3
-
從 G 到 C 最短路徑為 9
從圖上人工校驗可以知道 G 到 C 有兩條:
G → A → C:9 里G → E → C:12 里
證明演算法是正確的
-
…
-
最後一個 G 到 G,自己到自己,就是 0
-
換一個出發點驗證
這裡換一個觸發點 C 來看看執行結果
/**
* 從 c 出發
*/
@Test
public void dijkstraTest2() {
int[][] weights = new int[][]{
// A B C D E F G
/*A*/ {N, 5, 7, N, N, N, 2},
/*B*/ {5, N, N, 9, N, N, 3},
/*C*/ {7, N, N, N, 8, N, N},
/*D*/ {N, 9, N, N, N, 4, N},
/*E*/ {N, N, 8, N, N, 5, 4},
/*F*/ {N, N, N, 4, 5, N, 6},
/*G*/ {2, 3, N, N, 4, 6, N}
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
System.out.printf("共有 %d 條邊 \n", mGraph.edgeNum);
dijkstra(mGraph, 'C');
}
測試輸出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
共有 10 條邊
[true, true, true, true, true, true, true]
[2, 0, 100000, 5, 2, 4, 0]
[7, 12, 0, 17, 8, 13, 9]
從 C 到以下點的最短距離為:
A(7) B(12) C(0) D(17) E(8) F(13) G(9)

驗證幾個:
- 從 C 到 A 最短路徑為 7
- 從 C 到 B 最短路徑為 12
- CAB:12
- CEGB:15
- CAGB:12,雖然有相同的,但是還是最短的
- ….
- 從 C 到 C 最短路徑為 0
- …
- 最後一個 C 到 G 最短路徑為 9


