演算法中的複雜度分析
- 2021 年 10 月 3 日
- 筆記
複雜度
前言
來複習下,演算法體重經常聊到的複雜度
演算法中我們經常會從兩個角度去考慮演算法的優劣,那就是【時間維度】和【空間維度】
時間複雜度
時間複雜度:就是執行當前演算法消耗的時間。
當然我們這裡講的時間複雜度是個更加通用的描述,因為我們知道程式碼在不同中機器中執行的時間是不同的,性能好的機器可能就用的時間更短。
所以我們這裡的時間複雜度,用的是【大O符號表示法】,即T(n) = O(f(n))
如何理解呢?先來個栗子
func sum(n int) int {
sum :=0
i:=3
for m:=0;m<n;m++ {
sum+=n*i+1
}
return sum
}
比如上面這段程式碼,循環了n次,那麼時間複雜度就是O(n),如何分析呢?
我們假定每行程式碼執行的時間是一個時間顆粒,那我們上面的例子,第2和3行一共兩個時間顆粒,4和5行就是2*n個時間顆粒,總共就是(2n+2)個時間顆粒。
當然這樣算下來時間複雜度是T(n) = O(2n+2),大 O 時間複雜度實際上並不具體表示程式碼真正的執行時間,而是表示程式碼執行時間隨數據規模增長的變化趨勢,所以,也叫作漸進時間複雜度(asymptotic time complexity),簡稱時間複雜度。
如果 n 很大時,而公式中的低階、常量、係數三部分並不左右增長趨勢,所以都可以忽略。也就是2n中的2和常量2都可以忽略,所以時間複雜度就是T(n) = O(n)
常數階O(1)
無論程式碼執行了多少行,只要是沒有循環等複雜結構,那這個程式碼的時間複雜度就都是O(1),如:
func sum(n int) int {
sum :=0
i:=3
sum=sum*i
return sum
}
因為這段程式碼中沒有一個係數,會導致程式碼的執行時間隨係數的變化而變化,所以不管這個程式碼有多少行,都可以時間複雜度是 O(1)
一般情況下,只要演算法中不存在循環語句、遞歸語句,即使有成千上萬行的程式碼,其時間複雜度也是Ο(1)。
線性階O(n)
比如我們剛開始的這個例子
func sum(n int) int {
sum :=0
i:=3
for m:=0;m<n;m++ {
sum+=n*i+1
}
return sum
}
程式碼中有個 for 循環,程式碼的執行時間會因為 n 的變化而變化,並且是線性增加或減少,所以這裡用 O(n) 來表示他的時間複雜度。
對數階O(logN)
func sum(n int) int {
sum :=0
for sum<n {
sum+=n*2
}
return sum
}
這裡同樣也是一個循環,只不過每次都乘以2。也就是2的 x 次方大於等於 n 。 執行的次數就是 x 。
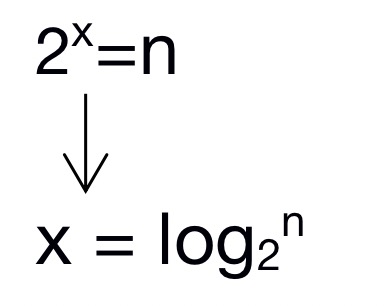
接著上面轉換的結果,對於省略掉常數2,所以時間複雜度就是 O(logN)
實際上,不管是以2為底、以3為底,還是以10為底,我們可以把所有對數階的時間複雜度都記為 O(logn)
線性對數階O(nlogN)
將上面的程式碼實例,外面在循環 n 次,時間複雜度就是下面我們要討論的 O(nlogN)
func sum(n int) int {
sum :=0
for i:=0;i<n;i++{
for sum<n {
sum+=n*2
}
}
return sum
}
這個就不展開討論了,內層循環是上面我們討論的 O(logN) ,外面多了一層循環,所以時間複雜度就是 O(nlogN)
平方階O(n²)
這個就很好理解了,就是兩層程式碼的循環
func sum(m,n int) int {
sum :=0
for i:=0;i<m;i++{
for j:=0;j<n;j++ {
sum+=j
}
}
return sum
}
當然有三層循環就是 O(n³),依次類推
空間複雜度
空間複雜度全稱就是漸進空間複雜度(asymptotic space complexity),表示演算法的存儲空間與數據規模之間的增長關係。
來個栗子分析下
func test(n int) map[int]struct{} {
testMap := make(map[int]struct{}, n)
for i := 0; i < n; i++ {
testMap[i] = struct{}{}
}
return testMap
}
比如上面的這段程式碼,空間複雜度是 O(n)
我們可以看到 for 開始的時候申請了一個變數 i ,這是常量級別的,跟數據規模 n 沒有關係,所以我們可以忽略。我們初始化了一個長度為 n 的 testMap。testMap 的長度會根據 n 的變化而變化,所以這段程式碼的空間複雜度就是 O(n)。
常數階O(1)
這個很簡單
func sum(n int) int {
sum :=0
i:=3
sum=sum*i
return sum
}
因為沒有變數跟隨數據規模 n 的變化而變化,所以空間複雜度就是 O(1)。
平方階O(n²)
看個栗子
func test(n int) [][]int {
var sil = make([][]int, n)
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
sil[i] = append(sil[i], j)
}
}
return sil
}
定義了二維切片,隨著兩層循環,分別申請了 n*n 個空間的大小,所以空間複雜度就是 O(n²)
當然有二維切片就是 O(n³),依次類推
最好、最壞情況時間複雜度
最好情況時間複雜度就是,在最理想的情況下,執行這段程式碼的時間複雜度。
最壞情況時間複雜度就是,在最糟糕的情況下,執行這段程式碼的時間複雜度。
比如這段程式碼
func sum(n, m int) int {
sum := 0
for i := 0; i < n; i++ {
if sum == m {
return sum
}
sum += i * 2
}
return sum
}
如果在第一次循環的時候,sum == m 就結束程式,那麼這個時候的時間複雜度就是最好時間複雜度。
當然如果上面的 for 循環,遍歷到最後一次也沒滿足 sum == m,那麼這個時候的時間複雜度就是最壞情況時間複雜度。
平均情況複雜度
顧名思義就是,最好和最壞的時間複雜度的平均值。
比如上面的那個例子
引入概率之後,前面那段程式碼的加權平均值為(3n+1)/4。用大O表示法來表示,去掉係數和常量,這段程式碼的加權平均時間複雜度仍然是O(n)。
均攤時間複雜度
對一個數據結構進行一組連續操作中,大部分情況下時間複雜度都很低,只有個別情況下時間複雜度比較高,而且這些操作之間存在前後連貫的時序關係,這個時候,我們就可以將這一組操作放在一塊兒分析,看是否能將較高時間複雜度那次操作的耗時,平攤到其他那些時間複雜度比較低的操作上。而且,在能夠應用均攤時間複雜度分析的場合,一般均攤時間複雜度就等於最好情況時間複雜度。
其實也可以認為均攤時間複雜度就是一種特殊的平均時間複雜度。
總結
這裡大概介紹了空間複雜度和時間複雜度
時間複雜度的全稱是漸進時間複雜度,表示演算法的執行時間與數據規模之間的增長關係。類比一下,空間複雜度全稱就是漸進空間複雜度(asymptotic space complexity),表示演算法的存儲空間與數據規模之間的增長關係。
這裡的計算使用的是【大 O 複雜度表示法】,時間複雜度和空間複雜度只和數據規模 n 有關係,公式中的低階、常量、係數三部分不影響增加趨勢,所以不收這三個的影響。
參考
【演算法的時間與空間複雜度(一看就懂)】//zhuanlan.zhihu.com/p/50479555
【數據結構與演算法之】//time.geekbang.org/column/intro/100017301
【空間複雜度和時間複雜度】//boilingfrog.github.io/2021/10/03/演算法中的複雜度分析/


