分組密碼（五）AES演算法② — 密碼學複習（八）

2021 年 9 月 30 日
筆記
密碼學複習

在上一篇簡單複習了AES的歷史時間節點、產生背景、與DES的對比、演算法框圖（粗略）以及一些數學基礎，如果不記得的話點擊這裡回顧。下面將介紹AES演算法的細節。

下面給出AES演算法的流程，圖片來源：密碼演算法詳解——AES。

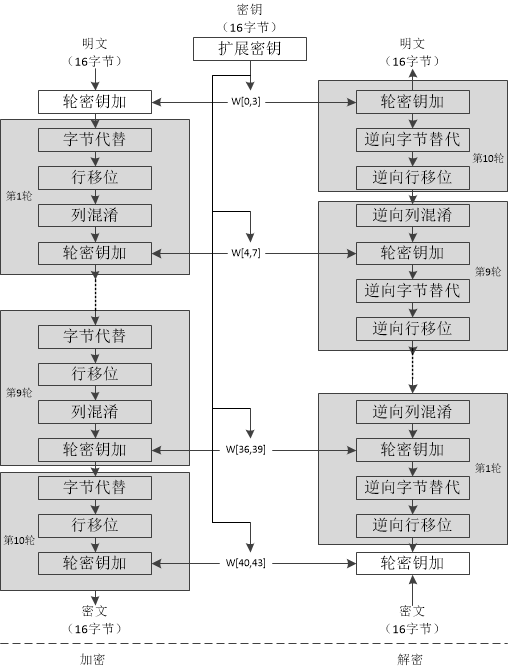
通過上圖可以知道，AES的加密演算法主要可以概括為：

① 一個初始輪密鑰加變換

② Nr-1輪的標準輪變換

③ 最後一輪的非標準輪變換

注意：

① 第一步和最後一步都用了輪密鑰加，因為沒有密鑰參與的變換都是容易被攻破的。

② DES的IP和IP^-1都沒有密鑰的參與。

8.1 輪變換 —— 加密輪函數

下面用偽程式碼的形式對其過程進行介紹。在AES中，除最後一輪外，其它輪次都是運行標準輪函數，最後一輪運行非標準輪函數。

① 標準輪變換

1 Round(State,RoundKey)
2 {
3     ByteSub(State);                 // S盒變換
4     ShiftRow(State);                // 行移位變換
5     MixColumn(State);               // 列混合變換
6     AddRoundKey(State,RoundKey);    // 輪密鑰加變換
7 }

② 最後一輪，非標準輪函數

1 FinalRound(State,RoundKey)
2 {
3     ByteSub(State);                 // S盒變換
4     ShiftRow(State);                // 行移位變換
5     AddRoundKey(State,RoundKey);    // 輪密鑰加變換
6 }

通過程式碼可以發現：最後一輪是沒有列混合的。

8.1.1 S盒變換 ByteSub(State)

① S盒變換是AES的唯一的非線性變換，是AES安全的關鍵。

② AES使用16個相同的S盒，DES使用的是8個不同的S盒。

③ AES的S盒有8位輸入，8位輸出，是一種非線性置換；DES的S盒有6位輸入，4位輸出，是一種非線性壓縮。

S盒變換可分為2步：（1）求逆；（2）代入公式計算。

（1）第一步：

把輸入位元組用其GF(2⁸)的逆來代替；

把輸入位元組看成GF(2⁸)上的元素；

求出其在GF(2⁸)上的逆元素；

用該逆元素代替原輸入位元組。

（2）第二步：

對上面的結果做如下仿射變換：

注意：

S盒變換的第一步是把位元組的值用它的乘法逆來代替，是一種非線性變換。
第二步是仿射運算，是線性變換。
由於係數矩陣中每列都有5個1，說明改變輸入任意一位，輸出中5位發生變化。
由於係數矩陣中每行都有5個1，說明輸出的每一位都與輸入的5位相關。

8.1.2 行移位變換 ShiftRow(State)

① 行移位變換對狀態的行進行循環移位；

② 第0行不移位，第1行移C1位元組，第2行移C2位元組，第3行移C3位元組。

Nb	C1	C2	C3
4	1	2	3
6	1	2	3

③ 行移位屬於置換，屬於線性變換。本質在於把數據打亂重排，其擴散作用。

8.1.3 列混合變換 MixColumn(State)

① 列混合變換把狀態的列視為GF(2⁸)上的多項式a(x)乘以一個固定的多項式c(x),並模x⁴+1.

b(x) = a(x)c(x) mod x⁴+1

其中，c(x)= 03x³+01x²+01x+02.

② 列混合變換屬於線性變換，起擴散作用。

③ c(x)與x⁴+1互素，從而保證c(x)存在逆多項式d(x),而c(x)d(x)=1 mod x⁴+1，只有逆多項式存在，才能進行解密。

寫成矩陣的形式：

8.1.4 輪密鑰加變換 AddRoundKey(State,RoundKey)

① 把輪密鑰與狀態進行模2相加

② 輪密鑰根據密鑰產生演算法產生

③ 輪密鑰長度等於數據塊長度

8.2 輪密鑰的產生

① 加密迭代中每一輪需要一個輪密鑰參與加密

② 輪密鑰根據密鑰產生演算法通過用戶密鑰得到

③ 密鑰產生分兩步進行：

（1）密鑰擴展

（2）輪密鑰選擇

④ 密鑰擴展將用戶密鑰擴展為一個擴展密鑰

⑤ 密鑰選擇從擴展密鑰中選出輪密鑰

密鑰擴展的原理圖如下圖所示，圖片來源：密碼演算法詳解——AES。

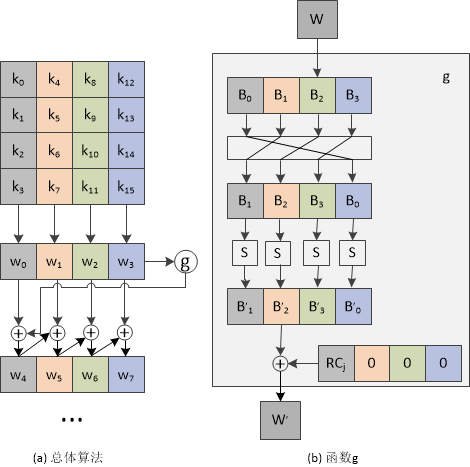
8.2.1 密鑰擴展

① 密鑰擴展產生擴展密鑰。

② 用一個字元素的一維數組W[Nb*(Nr+1)]表示擴展密鑰。

③ 用戶密鑰放在該數組最開始的Nk個字中。

④ 其它的字由它前面的字經過處理後得到。

⑤ 分Nk≤6和Nk＞6兩種密鑰擴展演算法。

（1）Nk ≤ 6的密鑰擴展

① 最前面的Nk個字是由用戶密鑰填充的

② 之後的每一個字W[j]等於前面的字W[j-1]與Nk個位置之前的字W[j-Nk]的異或

③ 而且對於Nk的整數倍的位置處的字，在異或之前，對W[j-1]進行Rotl變換和ByteSub變換，之後再異或一個常數Rcon.

當j不是Nk的整數倍：W_j=W_j-Nk⊕W_j-1

當j是Nk的整數倍：W_j=W_j-Nk⊕ByteSub(Rotl(W_j-1)⊕Rcon[j/Nk]

說明：

Rotl是一個字里的位元組循環左移函數：

設 W=(A,B,C,D) 則 Rotl(W)=(B,C,D,A)

輪常數Rcon與Nk無關，且定義為：

Rcon[i] = (RC[i],’00’,’00’,’00’)

RC[0] = ’01’

RC[i] = xtime(RC[i-1])

（2）Nk ＞ 6的密鑰擴展

說明：

Nk＞6的密鑰擴展與 Nk≤6的密鑰擴展基本相同，不同之處在於：如果j被Nk除的餘數=4，則在異或之前，對W[j-1]進行ByteSub變換。

增加ByteSub變換是因為當Nk＞6時密鑰很長，僅僅對Nk的整數倍的位置處的字進行ByteSub變換，就顯得ByteSub變換的密度比較稀，安全程度不夠強。

8.2.2 輪密鑰的選擇

根據分組大小，依次從擴展密鑰中取出輪密鑰。

前面的Nb個字作為輪密鑰0，接下來的Nb個字作為輪密鑰1…

8.3 AES的基本逆變換

AES的加密演算法不是對合運算，所以解密演算法和加密演算法不同。

AES的巧妙之處：雖然解密演算法和加密演算法不同，但解密演算法與加密演算法的結構相同。

把加密演算法的基本變換換成逆變換，便得到解密演算法。

AES的基本變換都是可逆的：

① 輪密鑰加的逆就是其本身：(AddRoundKey)^-1 = AddRoundKey

② 行移位變換的逆就是狀態的後三行分別移位Nb-C1、Nb-C2、Nb-C3個位元組。

③ 列混合的逆

狀態的每列都乘以c(x)的逆多項式d(x)：

d(x) = (c(x))^-1 mod x⁴+1

c(x) = 03x³+01x²+01x+02

d(x) = 0Bx³+0Dx²+09x+0E

④ S盒變換的逆

第一步：首先進行逆仿射變換；

第二步：再把每個位元組用其在GF(2⁸)上的逆來代替。

（1）把輸入位元組看成GF(2⁸)上的元素

（2）求出其在GF(2⁸)上的逆元素

（3）用該逆元素代替原輸入位元組

註：S盒的逆仿射變換：

⑤ 解密的密鑰擴展

解密的密鑰擴展與加密的密鑰擴展不同，解密的密鑰擴展定義如下：

（1）加密演算法的密鑰擴展

（2）把InvMixColumn（逆列混合）應用到除第一和最後一輪外的所有輪密鑰上。

⑥ 逆輪變換

（1）標準擬輪變換

1  Inv_Round(State,RoundKey)
2  {
3      Inv_ByteSub(State);             // S盒變換的逆
4      Inv_ShiftRow(State);            // 逆行移位變換
5      Inv_MixColumn(State);           // 逆列混合變換
6      AddRoundKey(State,RoundKey);    // 輪密鑰加變換
7  }

（2）最後一輪，非標準逆輪函數

1  Inv_FinalRound(State,RoundKey)
2  {
3      Inv_ByteSub(State);             // S盒變換的逆
4      Inv_ShiftRow(State);            // 逆行移位變換
5      AddRoundKey(State,RoundKey);    // 輪密鑰加變換
6  }

8.4 AES的實現

實現方法：軟體、硬體

軟體方法：

① 基於演算法的描述 —— 效率不夠高

② 基於查表 —— 時空折換，提高效率

基於查表：

① S盒，本質上是8進8出，但要S盒和逆S盒2個表。

② 列混合變換

GF(2⁸)的非零元素構成循環群，可通過加法和查表實現乘法。逆列混合約理。

8.5 AES的安全性

能夠抵抗目前所有的已知攻擊。①窮舉攻擊 ②差分攻擊 ③線性攻擊 ④Square攻擊 ⑤側信道攻擊

目前已有低於窮舉複雜度的攻擊方法，但都還不能對AES構成本質的威脅。

8.6 AES的體現

AES體現了香農的密碼設計理論。

體現了公開設計的原則。

實踐是檢驗AES密碼安全性的唯一標準。

8.7 AES的優點

① 運算速度快

② 對記憶體的需求非常低，適合於受限環境

③ 分組長度和密鑰長度設計靈活

④ AES的密鑰長度比DES的密鑰長度要長，用窮舉法破譯較難

⑤ 很好的抵抗差分密碼分析和線性密碼分析的能力

Tags: 密碼學複習