CS:APP Chapter 6 存儲器層次系統-讀書筆記
存儲器層次系統
筆記,應該不是一個大而全的文件,筆記應該是提綱挈領,是對思想的匯總濃縮,如果追求詳實的內容反而是丟了初心。
電腦是抽象的,它的設計者努力讓電腦變得簡單,在設計上高度抽象,而電腦的存儲系統就是這樣一個對用戶透明的部分,程式設計師布恩那個直接操作記憶體的控制,但是可以通過理解記憶體的組織結構,運行特點編寫對記憶體友好的程式,編寫具有較好時間局部性,空間局部性的程式。
存儲器是多樣的,從高速快取 Cache 到主存,再到磁碟,機械硬碟,固態硬碟,他們是各有特色,一般來說,越接近 CPU 的存儲設備,價格約昂貴,成本越高,其容量也越小,而越靠近磁碟的存儲設備,價格越低,容量越大,一般而言,我們可以把k層的設備看作是k+1層設備的快取,例如 Cache 是主存到 CPU 之間的快取,而主存是磁碟的快取。
形成這種存儲結構的原因是電腦軟體程式具有局部性,它往往會在短時間之內訪問同一塊區域的數據,也就是說相對而言較少跳躍著使用數據,因此,使用一個較小容量的快取就能覆蓋一大片可能出現下一時刻要用的數據,進一步提高處理器獲取需要數據的效率。
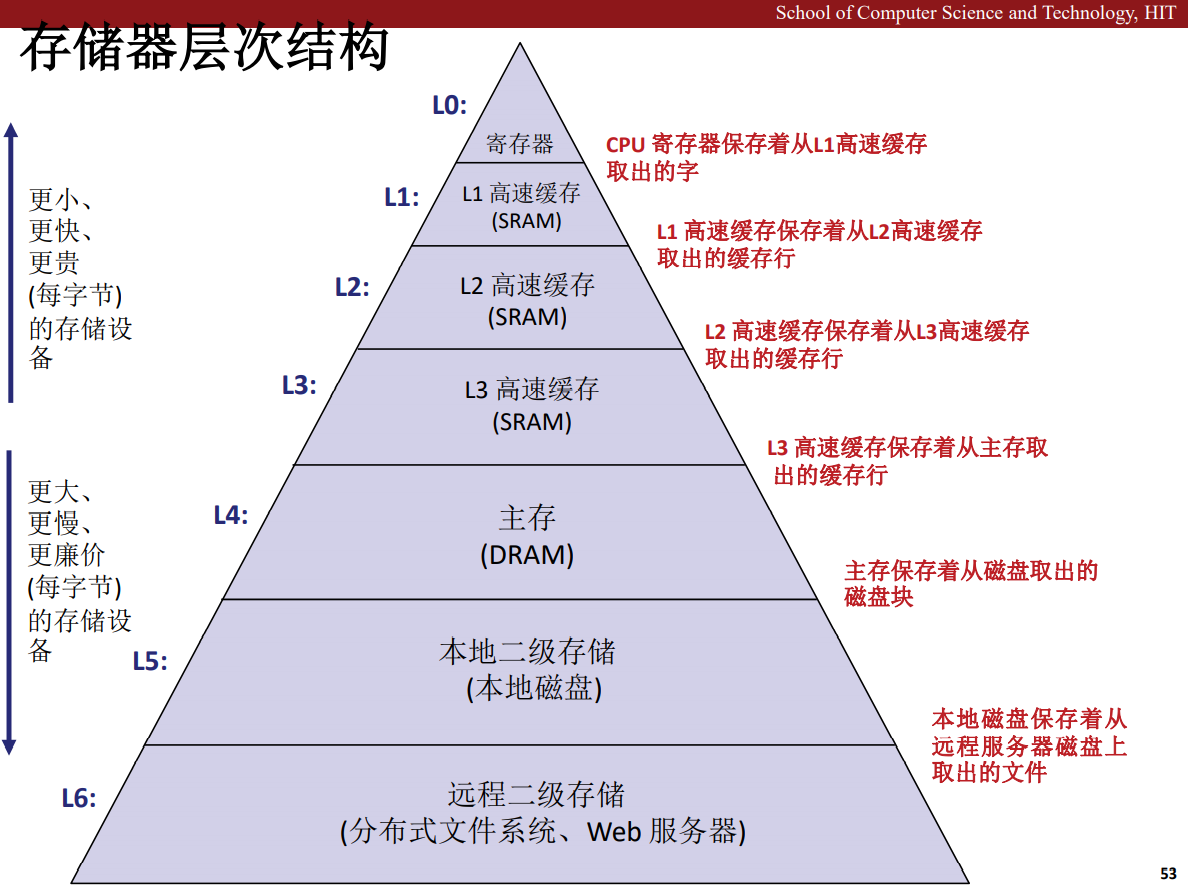
一般而言,所有的存儲設備的單位都是位元組,也就是 Byte 縮寫成 B,大寫。
機械硬碟
計算磁碟容量
容量 = (位元組數 / 扇區) * (平均扇區數 / 磁軌) * (磁軌數 / 面) * (面數 / 碟片) * (碟片數 / 磁碟)

這個計算比較簡單,只要把單位一個個約掉就行了。
從小到大分別是:位元組,扇區,磁軌,面,碟片,磁碟。
磁碟讀取

平均時間
$ 訪問時間 = 尋道時間 + 平均旋轉延遲(旋轉時間)+ 數據傳輸時間 $
尋道時間 (Seek time)
-
讀 / 寫頭移動到目標柱面所用時間,這個時間有可能是題目中直接給出的,我們無法計算尋道時間。
-
通常尋道時間為:3—9 ms
旋轉延遲 (Rotational latency)
-
旋轉盤面使讀 / 寫頭到達目標扇區上方所用時間
-
平均旋轉延遲 = 1/2 x 1/RPMs x 60 sec/1 min (RPM:轉 / 分鐘)
-
通常 平均旋轉延遲 = 7,200 RPMs
數據傳輸時間 (Transfer time)
-
讀目標扇區所用時間
-
數據傳輸時間 = 1/RPM x 1/(平均扇區數 / 磁軌) x 60 secs/1 min

每次讀取的是一個扇區,所以只需要計算讀取每個扇區的平均時間就行了,讀取的時間是遠遠小於磁頭的旋轉時間的。而且其中 \(\frac {60}{7200}(秒 / 磁軌)
\),注意這裡的單位,一個磁軌就是一個面的一整圈
設計使用高速快取
那麼,我們應該如何來設計一個高速快取系統呢?
-
了解電腦程式可利用的存儲特性:局部性。
-
使用不同的高速快取 – 主存映射方式來組織數據。
-
如何利用存儲器系統為我們準備好的局部性優化特點編寫快取友好的程式碼。
局部性
-
時間局部性(Temporal ):最近被訪問過的(指令或數據)可能會再次被訪問(比如循環,局部變數)
-
空間局部性(Spatial ):被訪問的存儲單元附近的內容可能很快也會被訪問(比如數組,順序訪問記憶體,順序讀取指令等)
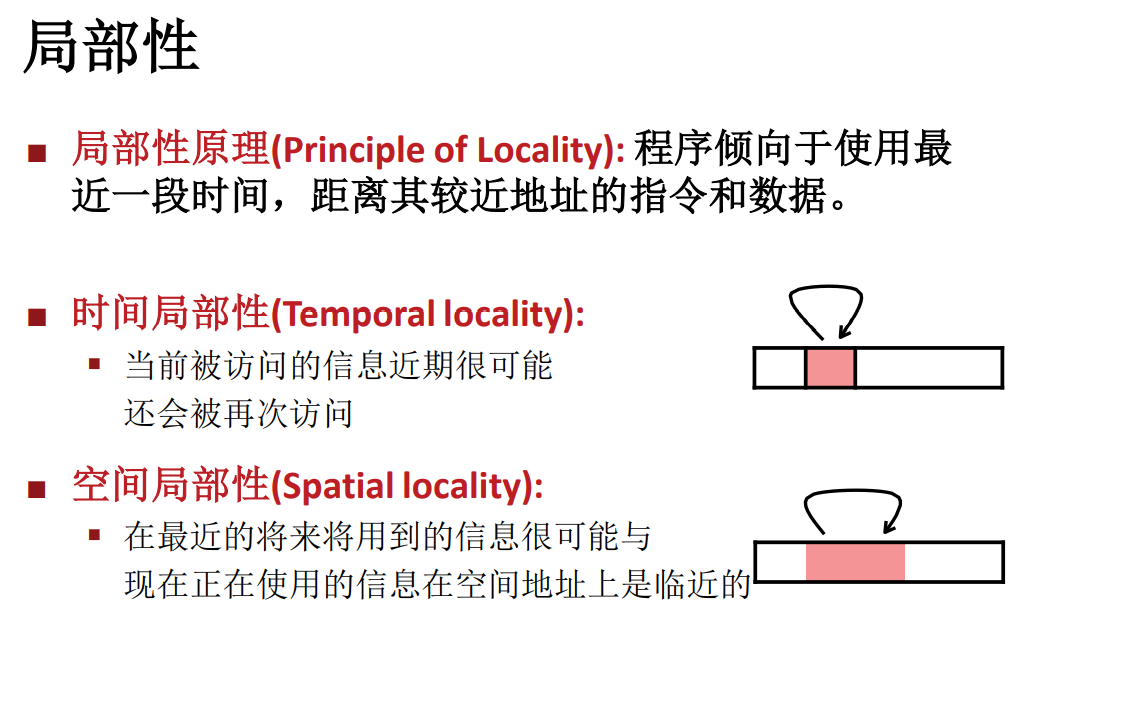
局部性說明,一段時間內,電腦往往傾向於訪問使用讀寫某一小塊的記憶體 / 數據,這塊數據以及這塊數據附近的數據都有比其他區域更高的使用概率,因此當我們快取這部分的時候就能讓效率得到更顯著的提升。
int sum_array_rows(int a[M][N])
{
int i, j, sum = 0;
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
sum += a[i][j];
return sum;
}
這段程式碼具有較好的空間局部性與時間局部性,因為這裡使用了一個局部變數來暫存加法的結果,並且其訪問數組的方式也是遵循數組在記憶體中存儲的特點,這讓快取能夠更加高效的命中。
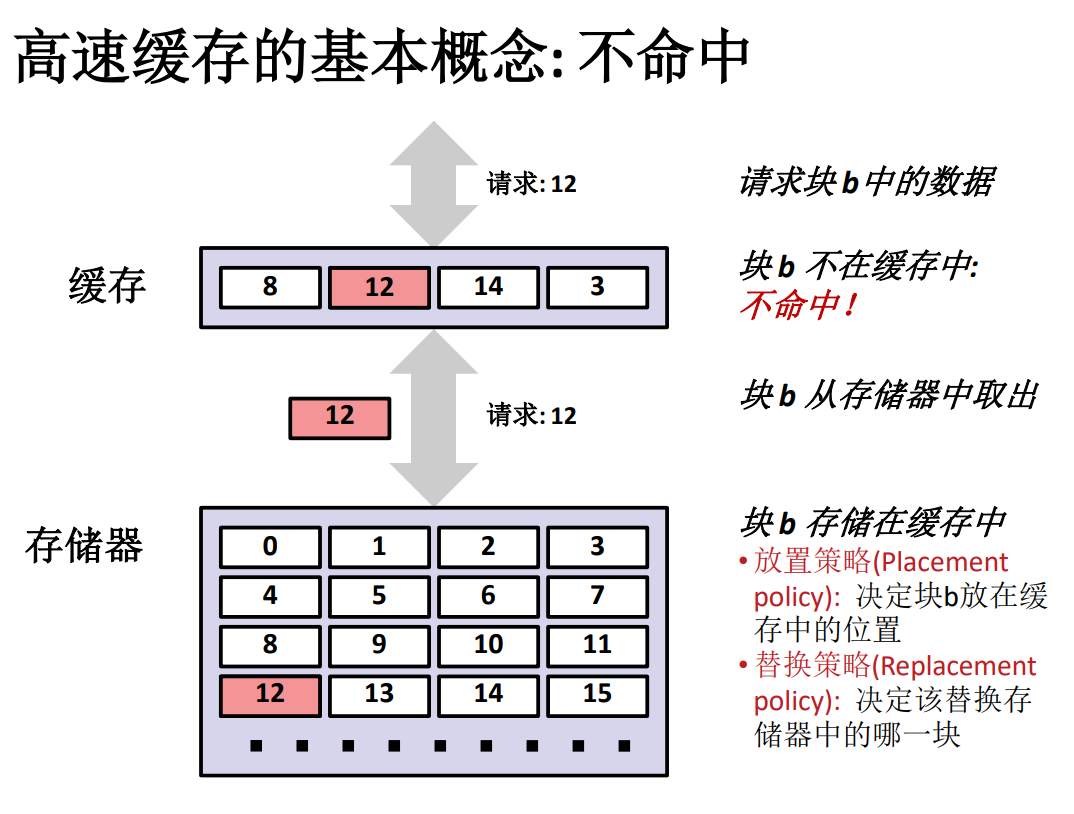
而事實上,總會出現快取不命中的情況,並且導致快取不命中的原因也有很多種。
快取不命中
-
冷不命中。當快取為空的時候,所有數據請求都不能在快取中找到對應的快取好的數據,一般來說這是在電腦剛剛啟動的時候才會發生這樣的情形。這種類型被稱為冷不命中。
-
衝突不命中。因為快取大小有限,而主存要比快取要大得多得多,因此不可能實現快取不重複地映射到所有主存單元,因此就會出現不同的主存單元映射到相同的快取塊中。例如某種快取映射策略為:第 k+1 層的塊 i 必須放置在第 k 層的塊 (i mod 4) 中,當快取足夠大,但是被引用的對象都映射到同一個快取塊中時候就是衝突不命中。衝突的例子:程式請求塊 0, 8, 0, 8, 0, 8, …. 這時每次請求都不命中。
-
容量不命中。處理器要處理的工作集的大小遠遠大於快取的大小時,計算把全部的工作集內容讀取到快取中來,也有可能發生不命中,此時被稱為容量不命中。
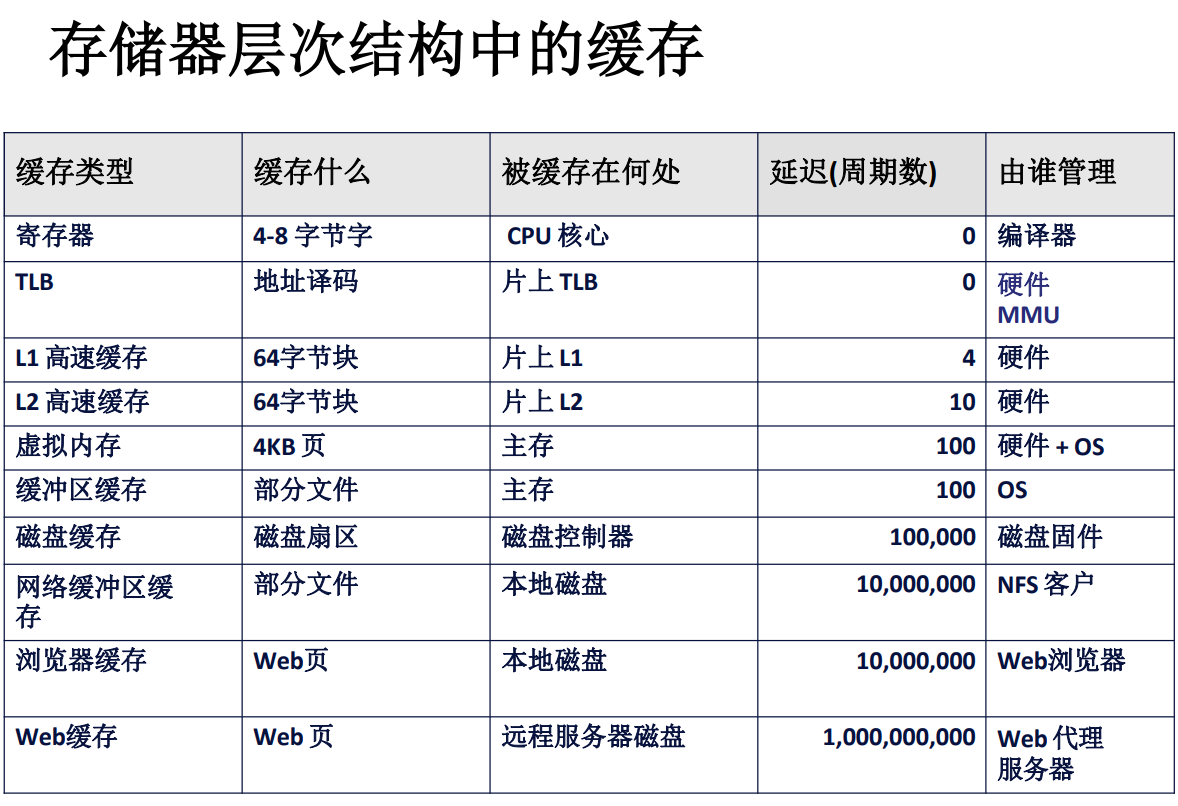
如果說第一部分的主要內容是磁碟,高速快取的概念的話,那第二部分就主要是高速快取的組織結構,以及如何利用高速快取針對性地編寫程式碼。

暫存器是最靠近計算單元的存儲設備,因此,它的讀取寫入速度也是所有設備中最快的,高速快取的速度稍慢,介於暫存器與記憶體之間,高速快取通過匯流排介面與外部的存儲設備溝通,經由系統匯流排、I/O橋、記憶體匯流排與主存相連接。
CPU 其實也並不需要了解快取到底是怎樣運作的,它只管給出自己當前需要的數據的主存地址,也就是說 CPU 只知道數據應該在記憶體里,而這個主存地址在傳輸過程中會經過高速快取,高速快取會自動判斷這個地址所代表的數據是否在快取中,一般來說是通過計算主存地址中的資訊,利用高速快取的映射策略來得到該地址在快取中對應的位置,並將主存地址中的 tag 與快取中那個位置的 tag 進行比較,如果一致就說明是對的。
但是並不是所有的主存內容都恰好在快取中,只有極少數的一部分(快取比主存要小的多的多)會存放在主存中。因此總會有沒命中的情況,在這種情況下就需要從主存中讀取需要的數據。
讀取完成之後有兩步並行操作,1️⃣ 是把 CPU 需要的數據趕緊送到 CPU 那裡去,2️⃣ 是把剛送過來的數據存放在快取中,因為電腦程式具有時間局部性,在不遠的未來有比較大的可能接著訪問這個記憶體單元,因此快取起來可以應對未來的讀取需求。

上面是高速快取系統的一個理想流程圖,要實現整個過程需要很多的細節方面的考量。
-
主存如何分塊,Cache 如何分塊或分區分行
-
主存塊與快取之間如何映射
-
如果快取放滿了的話如何淘汰快取中的塊
-
寫入主存的請求如何正確處理以保證快取與主存之間的一致性
-
如何根據主存地址計算快取中的數據位置並比對
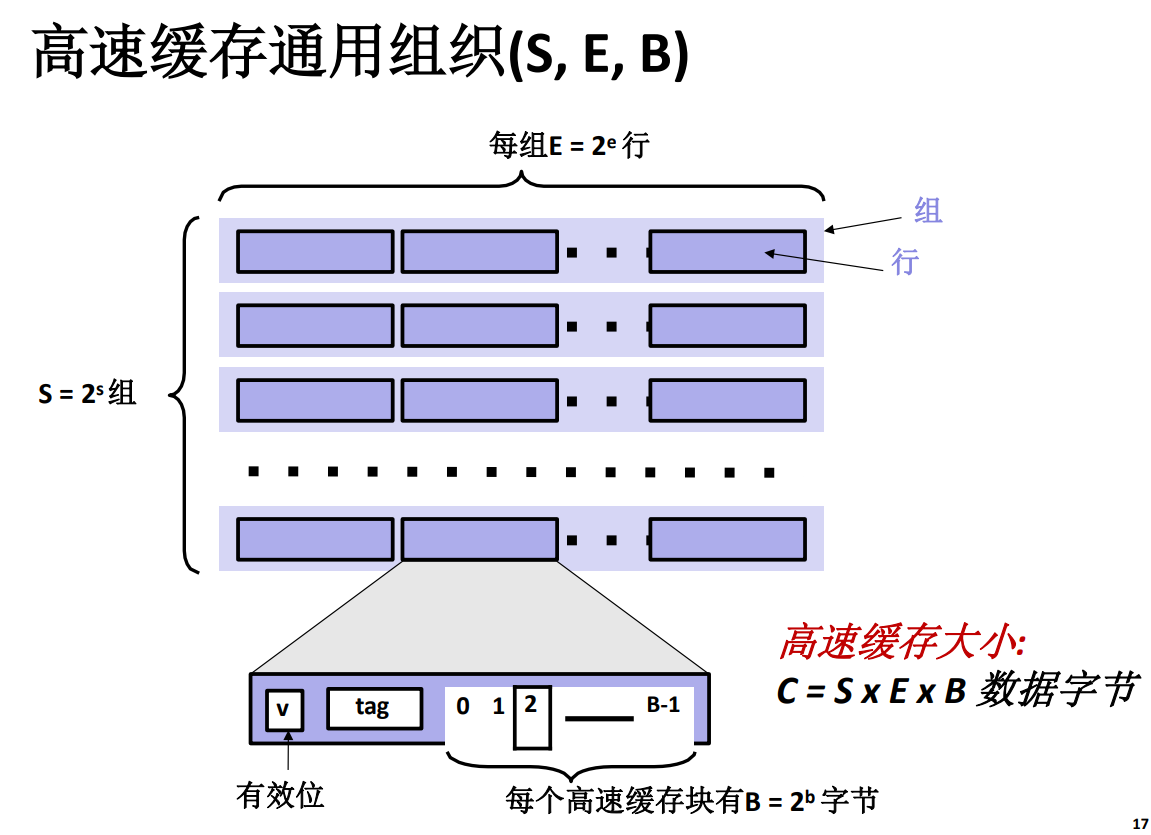
高速快取通用組織
-
S 代表 Cache Set,也就是快取組
-
E 代表 Cache Line,也就是快取行
-
B 代表組成每一行的數據塊的位元組數目 \(B=2^b\)。
要注意,高速快取中最大的分組就是 Cache Set,而主存地址中的 s 也就是組索引,而最小的數據包裹單位是數據行,包含真正數據的是數據塊,數據塊中沒有有效位,標記位之類的資訊,裡面只有數據!
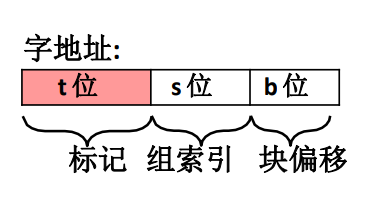
不管快取的映射策略是什麼樣的,CPU 發出的主存地址格式一定是一致的不會因為快取的映射策略而出現不同格式的主存地址,一般來說主存地址是由 3 部分組成。
-
\(t\) 代表標記
-
\(s\) 代表組索引
-
\(b\) 代表塊偏移量
當然這些不同部分在不同策略中的含義也是不一樣的。不過大體上都是這幾塊。
直接映射高速快取
這種映射策略的最主要特點是它每一個快取組中只有一個高速快取行,也就是 \(E=1\),代表每一個主存塊僅僅會映射到其中一個 Cache 的固定一行。
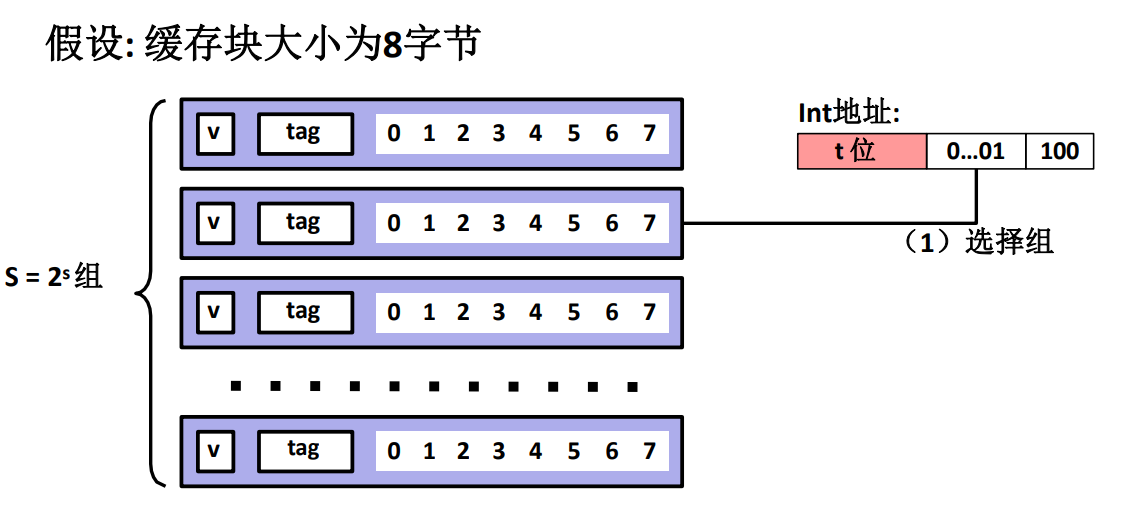
而每一行並不是每個位都是數據,而是也分成了很多部分。
-
\(v\) 代表有效位 \(valid\)。
-
\(tag\) 代表標記
-
之後的數字代表剩下的數據,所有數據代表了一個快取塊,它有 \(B\) 個位元組,而 CPU 需要的數據在哪個位元組由主存地址中的數據偏移量指出!
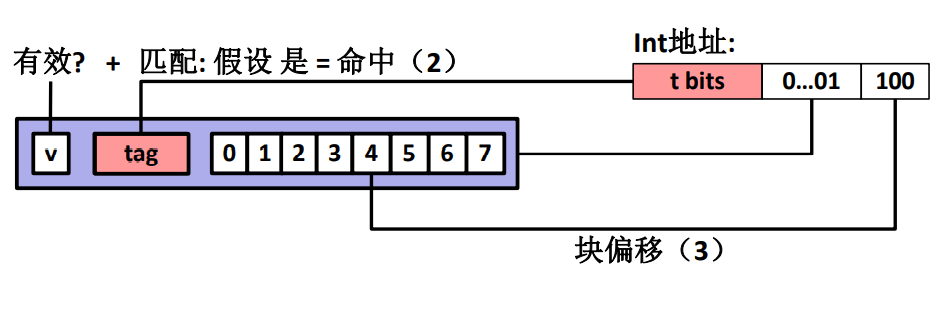
同時要注意,並不是只取出其中那一個位元組,100 代表的是 4,這個數字是要取出的數據的起始位置,然後根據數據類型計算剩下的數據長度,然後再把全部數據完整的拿出來。

-
有效的標記位
-
正確匹配的 tag
-
根據偏移量與數據類型長度取出數據
這樣三部分走完才算是完成了直接映射快取器的讀取過程。
如果沒有找到匹配的行,就從主存中讀取然後直接驅逐替換,不用考慮是否什麼優先順序的關係,反正只有一行。
E – 路組相聯高速快取
此處簡單取 \(E=2\) ,也就是每組有兩個數據行。
當使用 E – 路組相聯高速快取時,每個主存塊都映射到 Cache固定組的任意一行,有點像直接映射快取的鏈表,也就是每一個組裡面是一個鏈表!然後數據寫入的時候是先到先寫入,因此位置是不固定的。
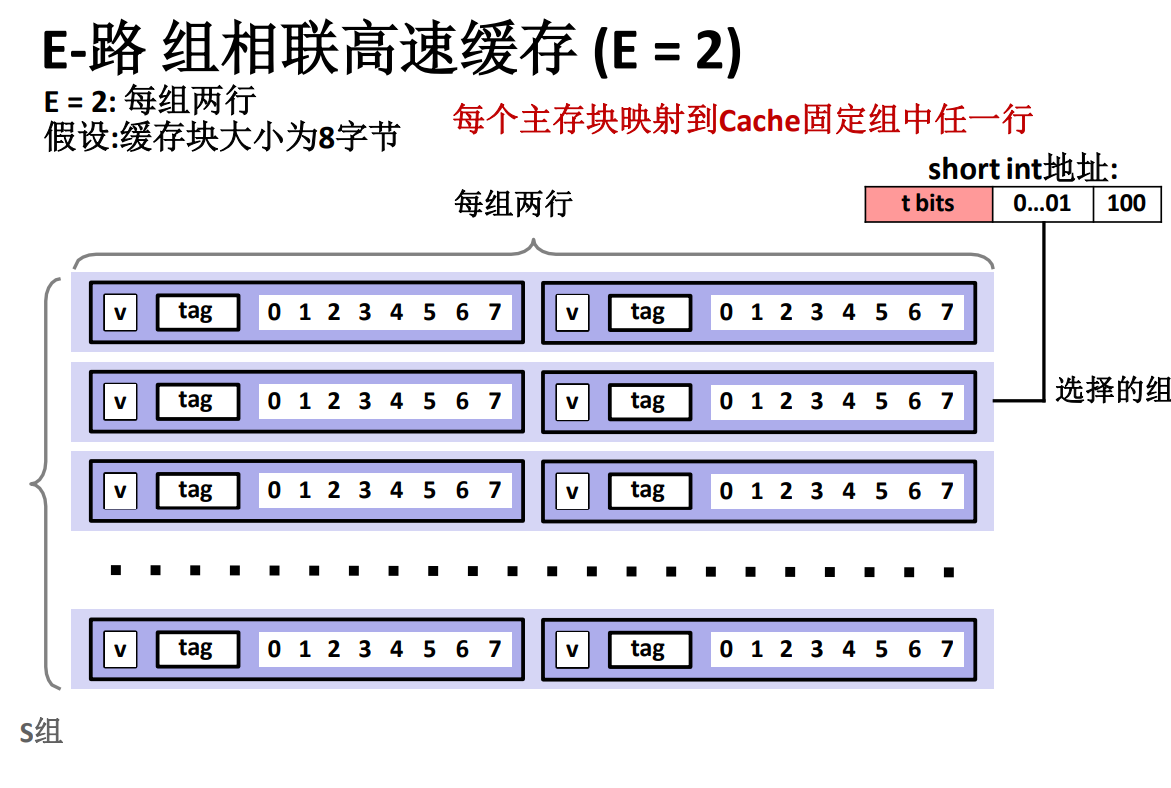
而 E – 路組相聯高速快取的查找過程跟直接組相聯也比較類似,不過它並不能保證 \(O (1)\) 的時間複雜度,因為對應的數據塊的位置並不是固定的,所以不會一下子直接找到,通過主存地址中的組索引 \(s\) 部分可以定位到這個主存塊對應的組,然後對這個組中所有的行進行遍歷,找到 tag 和主存地址中的 tag 一致的行,然後使用同樣的辦法讀取需要的數據。


當不匹配的時候,需要在主存地址給出的組中找到一行用來存放主存地址對應的那段數據,由於一個組中有多個行,所以要考慮驅逐替換哪一行!
替換策略:
-
隨即替換
-
替換最近最少使用的那行
高速快取的寫入問題
-
存在多個數據副本:
- L1, L2, L3, 主存,磁碟
-
在寫命中時要做什麼?
-
直寫 (立即寫入存儲器)
-
寫回 (推遲寫入記憶體直到行要替換)
- 需要一個修改位 (和記憶體相同或不同的行)
-
-
寫不命中時要做什麼?
-
寫分配 (載入到快取,更新這個快取行)
- 好處是更多的寫遵循局部性
-
非寫分配 (直接寫到主存中,不載入到快取中)
-
-
典型的
-
直寫 + 非寫分配
-
寫回 + 寫分配
-
高速快取實例
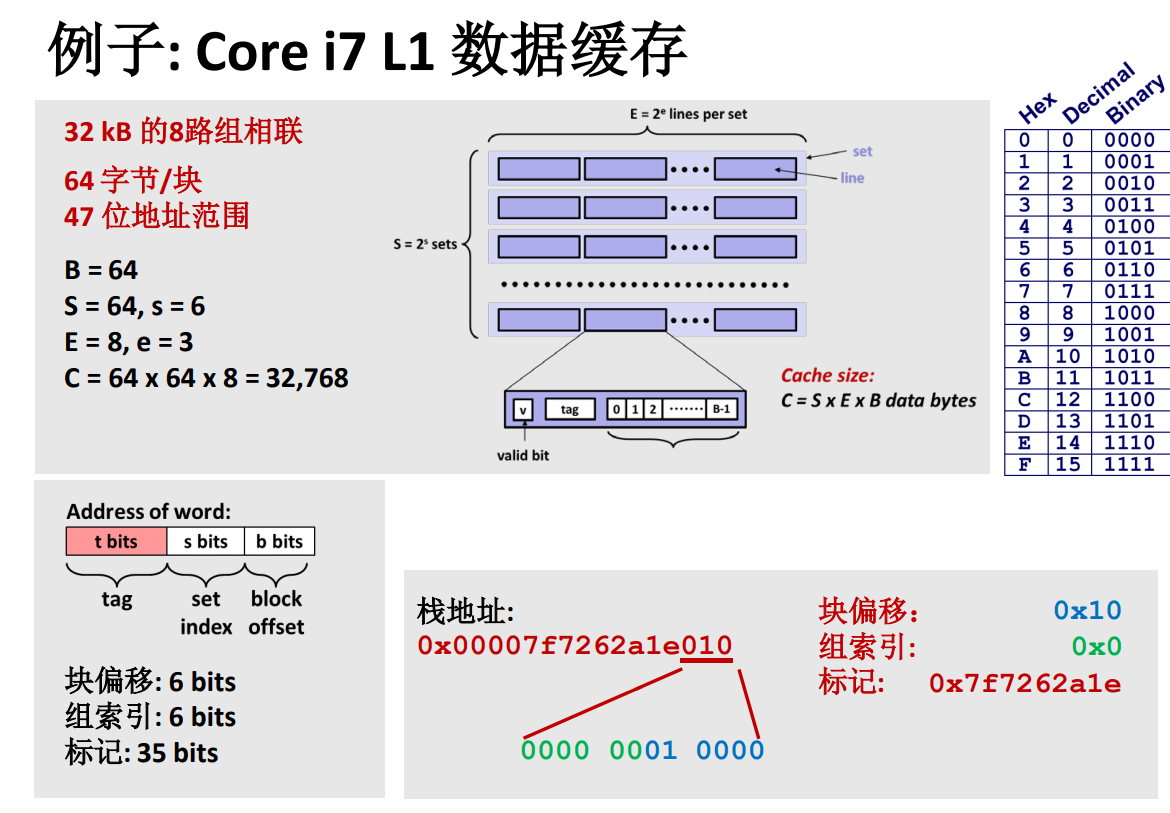
注意地址範圍只用了 47 位!
性能指標
高速快取中有許多指標用來衡量高速快取是否高效運行,我們可以使用這些標準來衡量我們寫的程式是否足夠高效!


吞吐量
每秒鐘從存儲系統中讀取 / 寫入的位元組數,單位是 \(MB/s\)。
存儲器山
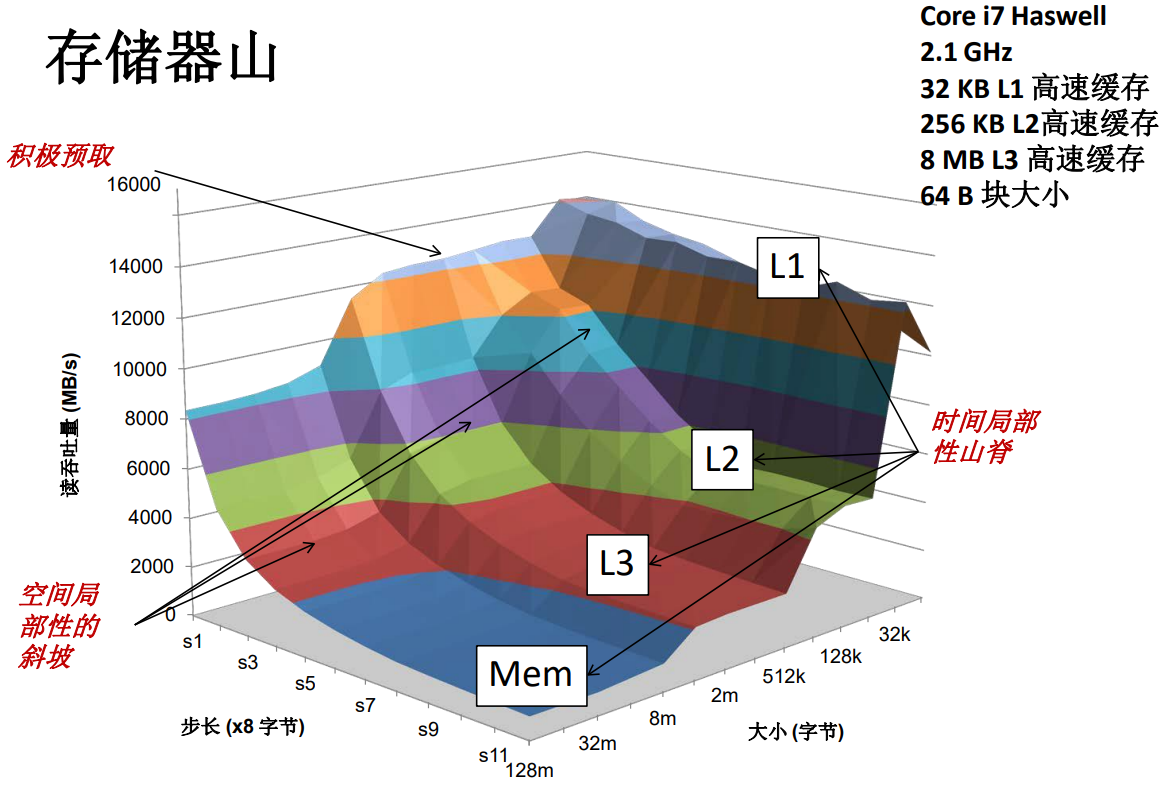
我們希望藉助一個簡單的程式來檢驗這個存儲器山的特性。
存儲器山測試函數
long data[MAXELEMS];
int test(int elems, int stride) {
long i, sx2=stride*2, sx3=stride*3, sx4=stride*4;
long acc0 = 0, acc1 = 0, acc2 = 0, acc3 = 0;
long length = elems, limit = length - sx4;
/* Combine 4 elements at a time */
for (i = 0; i < limit; i += sx4) {
acc0 = acc0 + data[i];
acc1 = acc1 + data[i+stride];
acc2 = acc2 + data[i+sx2];
acc3 = acc3 + data[i+sx3];
}
for(; i<length; i++) {
acc0 = acc0 + data[i];
}
return ((acc0 + acc1) + (acc2 + acc3));
}
矩陣乘法的例子

這個例子使用的演算法就是最樸素的矩陣乘法,左矩陣的行乘以右矩陣的列,然後將所有乘法的結果相加,得到 c 矩陣的一個元素。
矩陣不命中率分析
假設
- 塊大小為 32 個位元組 32Byte
- 矩陣的維數比較大
- 高速快取的一個塊不足以快取矩陣的一整行元素
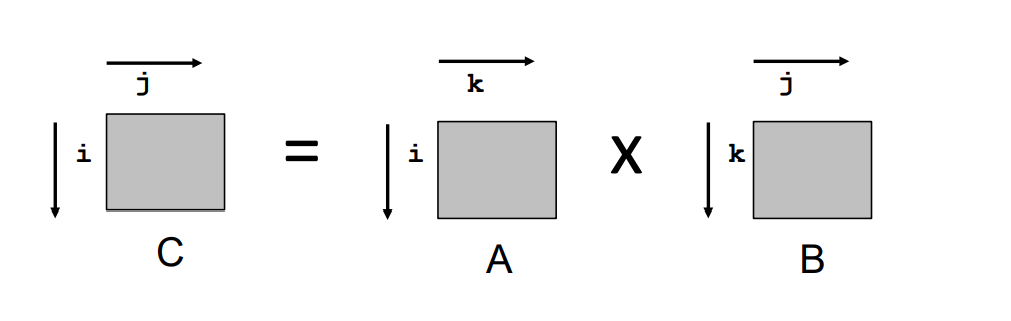
對於不同的記憶體訪問方式,有著不一樣的訪問命中率,首先要明確的是記憶體對數組是按照行進行存儲的,所以在行方向上存在命中的可能。

很顯然,每一行的總大小遠遠大於高速快取中一個快取塊的大小,因此快取塊一般來說是村放不下完整的一行的,因此按行掃描的時候命中率只有 \(1-(sizeof (a_{ij})/B)\),因此不命中率就是 \(sizeof (a_{ij})/B\),也就是說如果元素大小佔了整個存儲塊的一半,那麼它的不命中率就高大 \(50%\),因此可以看出當元素占的存儲空間越小,高速快取的命中率越高。
而按列掃描就不太可能命中,除了行很小,快取塊很大的情況。
矩陣乘法
此處的 \(ijk\) 代表了遍歷順序,也就是三個循環的順序,最外層是 \(i\),次外層是 \(j\),最內層是 \(k\)。
ijk
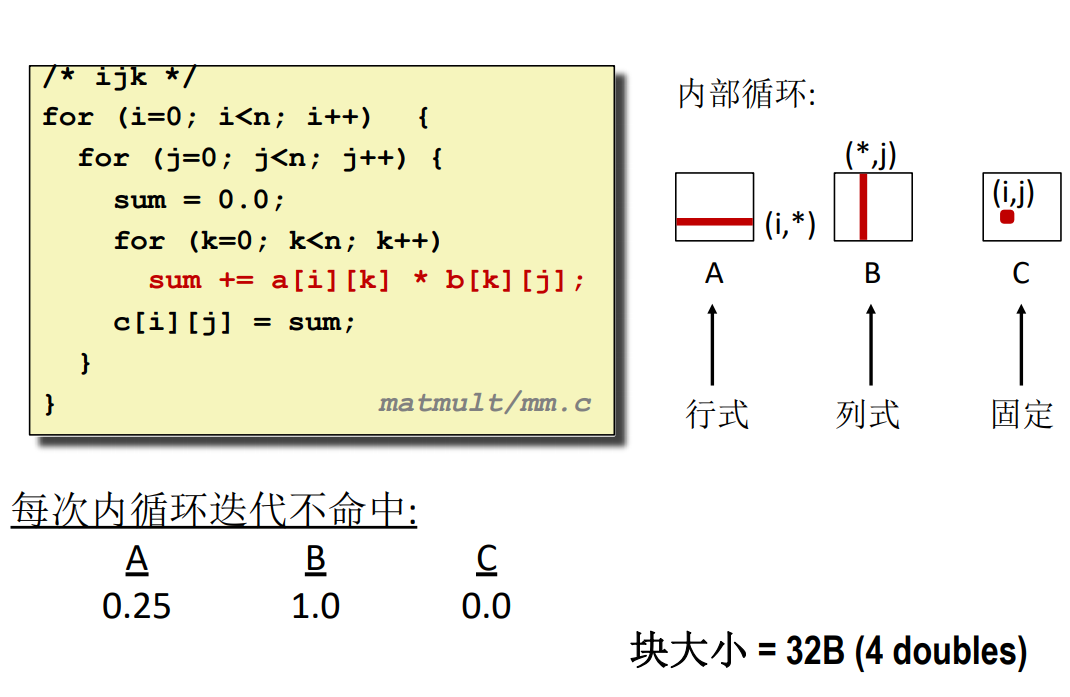
jik
這種做法跟 ijk 的完全一致,對於 B 的訪問都是按列訪問,所以不命中率都是 \(1.0\)。
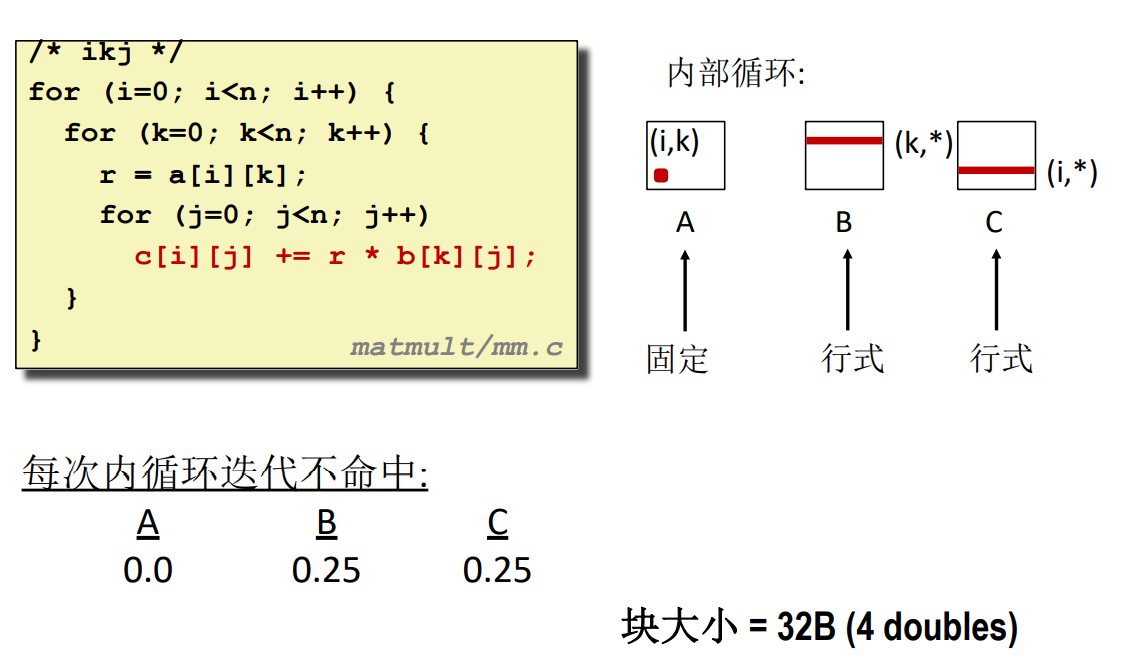
kij

這裡的演算法就完全是換了一個思路,並不直接使用矩陣乘法的定義,因為定義的演算法中肯定會存在按列遍歷,所以會有不命中率為 1 的情況,而這裡把乘法結果矩陣的每一個元素拆成多個元素相加(雖然本來就是這樣的,但這裡的相加不是一次性加完,而是一行一行的加)
例如一個二階方陣,它的左上角元素的表達式為 \(C[0][0]=A[0][0]*B[0][0]+A[0][1]*B[1][0]\),當使用上圖的演算法時,並不是一步算出來,而是通過兩次 \(k\) 的循環,第一次讓 \(C [0][0]=A[0][0]*B[0][0]\),第二次讓 \(C[0][0]+A[0][1]*B[1][0]\),注意 \(k\) 的每次循環中,都有與 \(C [0][0]\) 相關的表達式,也就是說最外層的循環每經歷一次,就會給 C 矩陣的所有位置加上一個數,而一共有 \(k\) 個乘法表達式,所以循環結束就是答案。
這裡有一個共通之處是,所有的訪問表達式都是:
\]
因此可以作為一個記憶點。
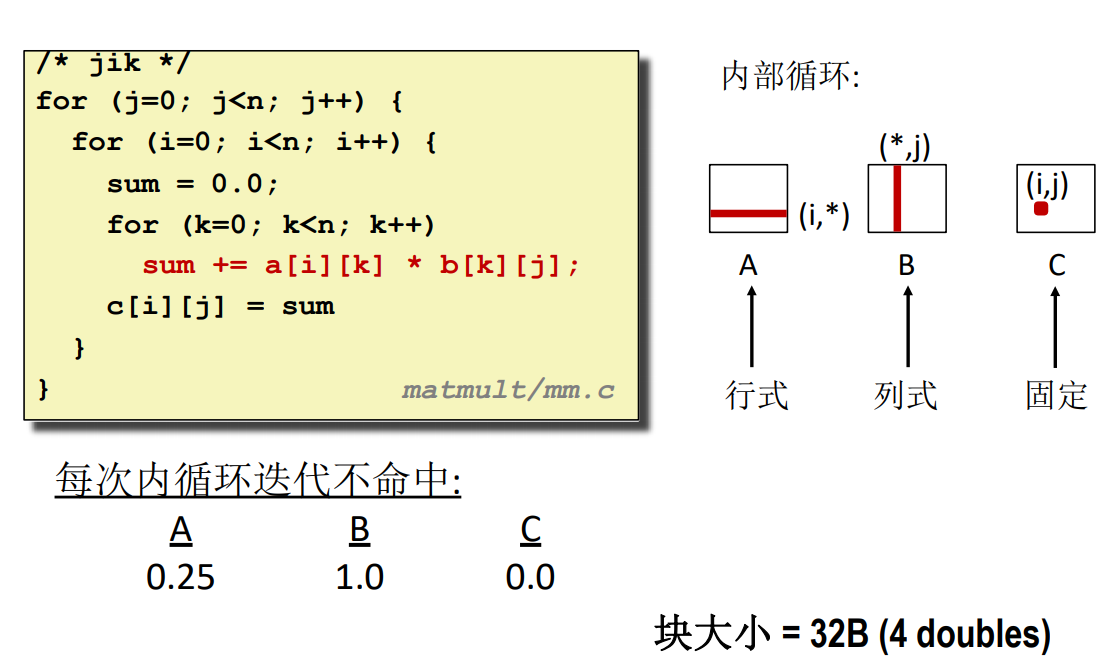
ikj
jki
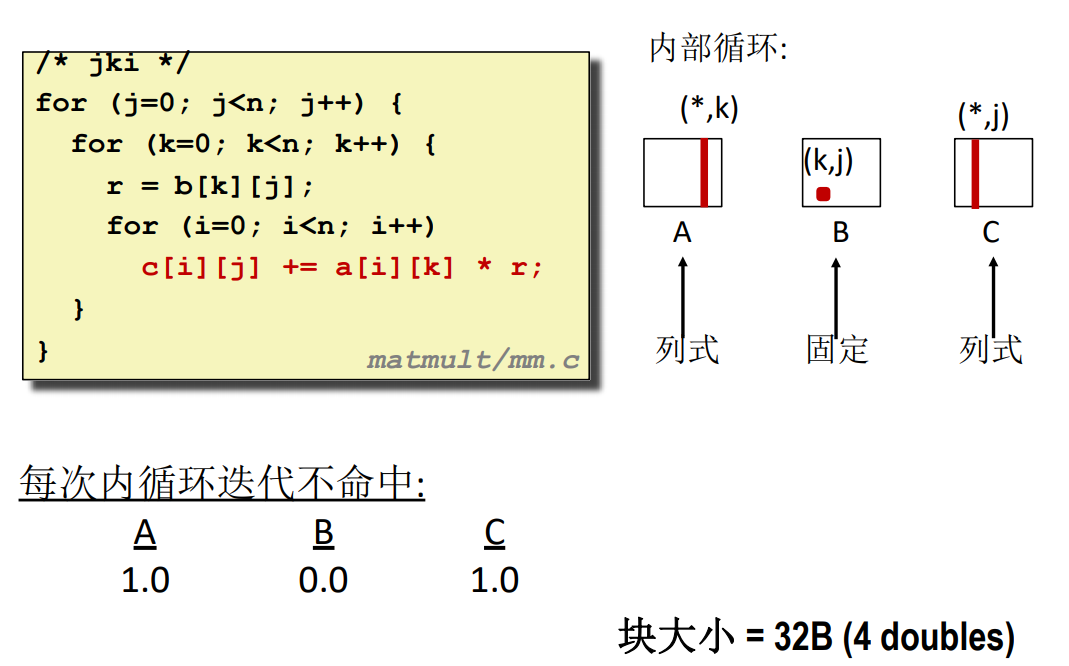
kji
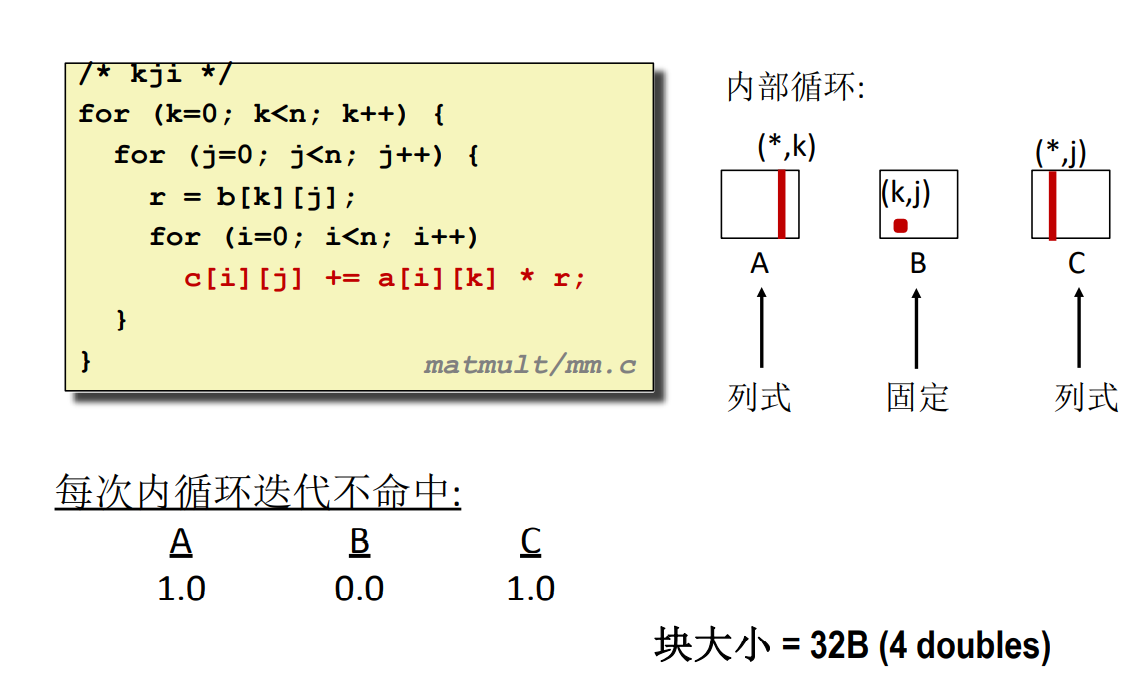
要看兩個數相乘的結果是哪個元素的一部分可以通過 \((i,k) 和 (k,j)\) 的組合,將中間的 k 消去,得到的就是對應的元素位置 \((i,j)\)。只要滿足這個表達式,不管怎麼乘,什麼時候加都是可以的。不同演算法實際上就是調整位置而已。
矩陣乘法總結

性能差異
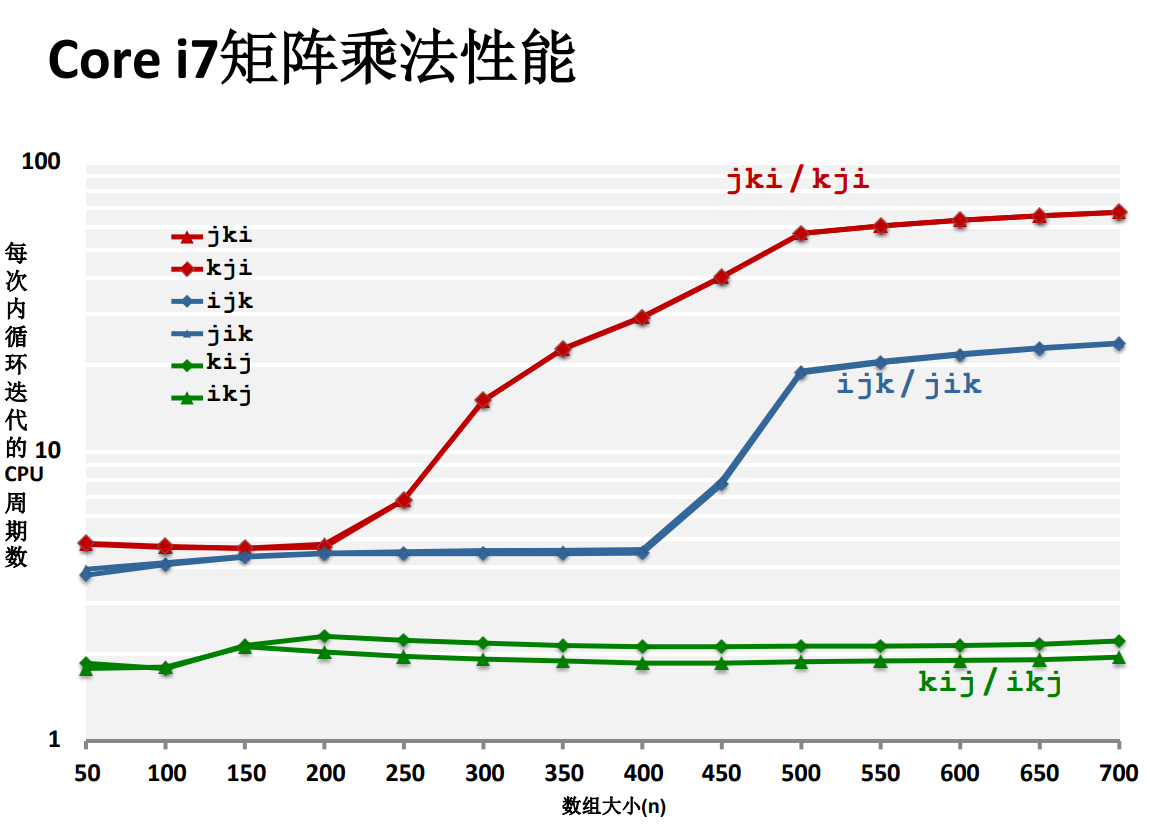
不命中率的理論分析
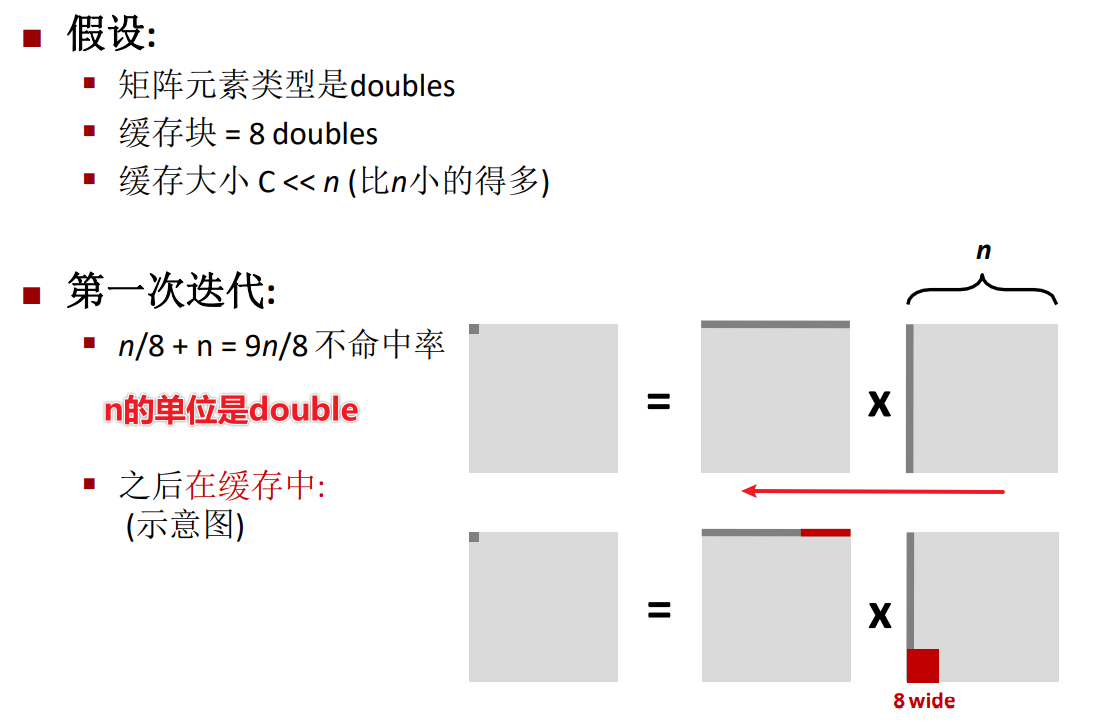
這裡等式兩邊交換了位置,\(\frac{n}{8}\)就是矩陣行的長度除以快取塊的長度,這裡我的一個猜測是,每個元素的大小是1個double,那麼一行有n個元素,而一個double元素的不命中率為\(\frac{1}{8}\),所以總的行不命中率就是\(\frac{n}{8}\)。
同樣的,第二次迭代的不命中率也是\(\frac{9n}{8}\),因此最後總的不命中率為\(\frac{9n^3}{8}\)。
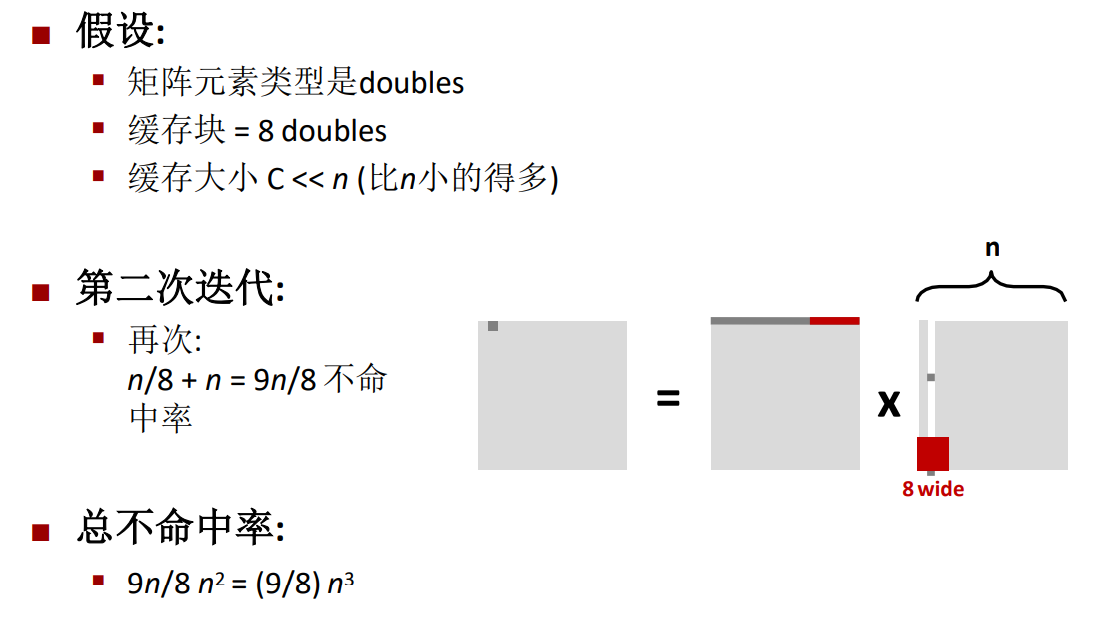
分塊矩陣
c = (double *) calloc(sizeof(double), n*n);
/* Multiply n x n matrices a and b*/
void mmm(double *a, double *b, double *c, int n)
{
int i, j, k;
for (i = 0; i < n; i+=B)
for (j = 0; j < n; j+=B)
for (k = 0; k < n; k+=B) /* B x B mini matrix multiplications */
for (i1 = i; i1 < i+B; i++)
for (j1 = j; j1 < j+B; j++)
for (k1 = k; k1 < k+B; k++)
c[i1*n+j1] += a[i1*n + k1]*b[k1*n + j1];
j1 c =i1 a * Block size B x B b + c;
}
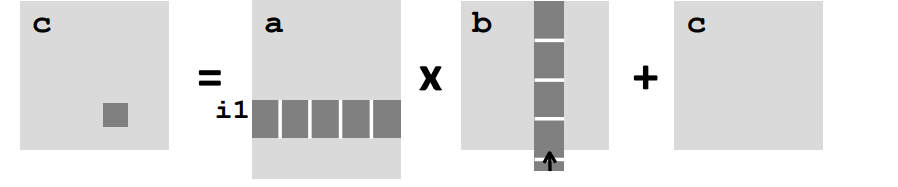
對此做出一定的假設,假設快取塊的大小是8 double,並且快取的總大小遠遠小於矩陣的行數,但是滿足約束條件\(3B^2<C\),也就是說最少可以放入三個分塊矩陣。
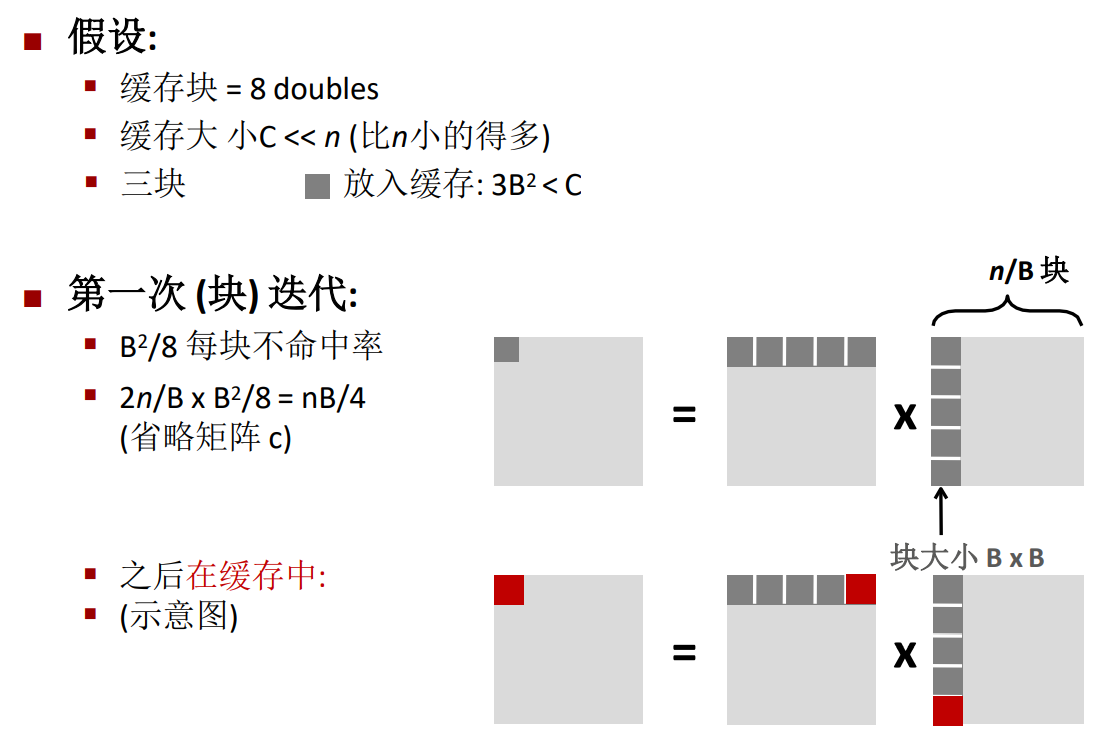
其中的\(\frac{2n}{B}\)代表每次運算的時候有這麼多的分塊矩陣參與運算,矩陣數量乘以每塊矩陣的不命中率,得到的就是第一次迭代的總的不命中率。
第二次迭代也是一樣。
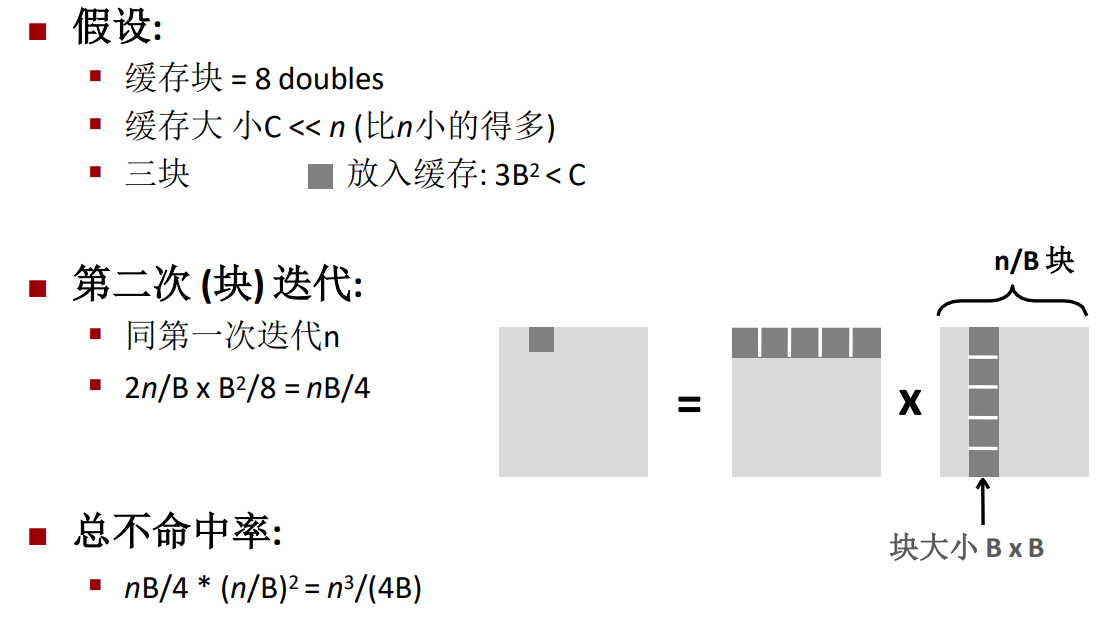
最後可以得到
-
不分塊的情況下,不命中率是\(\frac{9n^3}{8}\)。
-
分塊的情況下是\(\frac{n^3}{4B}\)。

