數據結構與演算法(十二)——演算法-動態規劃
一、青蛙跳台階&斐波那契數列
1、問題
一隻青蛙跳台階,每次可以跳 1 層或 2 層。青蛙跳到 n 層一共有多少種跳法?
2、思想
先把問題規模縮小,考慮 n = 1時,n = 2的解。那麼,顯然有:
(1)邊界條件:dp[1] = 1、dp[2] = 2
(2)再考慮 n = 3時,逆向思維一下,要跳 3 層,是不是只能是從第 2 階跳 1 層到或者是從第 1 階跳 2 層到。所以dp[3] = dp[2] + dp[1]。
(3)同理n = 4時,是不是也是只能是從第 3 階跳 1 層到或者是從第 3 階跳 2 層到。所以dp[4] = dp[3] + dp[2]。
(3)……
(4)同理可得,狀態轉移方程:dp[n] = dp[n – 1] + dp[n – 2]。

3、程式碼示例
1 // 遞歸.時間複雜度:O(2^n).空間複雜度:O(1) 2 public int jumpFloor(int target) { 3 if (target == 1) { 4 return 1; 5 } 6 if (target == 2) { 7 return 2; 8 } 9 10 return jumpFloor(target - 1) + jumpFloor(target - 2); 11 } 12 13 // 循環(dp數組).時間複雜度:O(n).空間複雜度:O(n) 14 public int jumpFloor2(int target) { 15 if (target == 1) { 16 return 1; 17 } 18 19 int[] dp = new int[target + 1]; 20 dp[1] = 1; 21 dp[2] = 2; 22 for (int i = 3; i <= target; i++) { 23 dp[i] = dp[i - 1] + dp[i - 2]; 24 } 25 return dp[target]; 26 } 27 28 // 滾動數組.時間複雜度:O(n).空間複雜度:O(1) 29 public int jumpFloor3(int target) { 30 if (target == 1) { 31 return 1; 32 } 33 int num1 = 1, num2 = 2, temp = num2; 34 35 for (int i = 3; i <= target; i++) { 36 temp = num1 + num2; 37 num1 = num2; 38 num2 = temp; 39 } 40 41 return temp; 42 }
二、網格路徑
1、問題
有一個 m*n 的網格,從 [1, 1] 出發,每次只能向右或向下,抵達 [m, n] 一共有多少種方案?如圖:

2、思想
先把問題規模縮小,考慮從 [1, 1]到 [1, 2],到 [1, 3],到 [1, 4]……和從 [1, 1]到[2, 1],到 [3, 1]……,是不是只能一直向右和向下,那麼,顯然有:
(1)邊界條件:dp[1][n] = 1、dp[m][1] = 1
(2)再考慮到 [2, 2] ,是不是只有 [1, 2] 向下或者 [2, 1] 向右。所以dp[2][2] = dp[1][2] + dp[2][1]。
(3)同理可得,狀態轉移方程:dp[m][n] = dp[m – 1][n] + dp[m][n – 1]。
3、程式碼示例
1 // 3*6. m=3,n=6 2 public static int gridPath(int m, int n) { 3 int[][] dp = new int[m + 1][n + 1]; 4 for (int i = 1; i <= n; i++) { 5 dp[1][i] = 1; 6 } 7 8 for (int i = 1; i <= m; i++) { 9 dp[i][1] = 1; 10 } 11 12 // 遍歷二維數組 13 for (int i = 2; i <= m; i++) { 14 for (int j = 2; j <= n; j++) { 15 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; 16 } 17 } 18 19 return dp[m][n]; 20 }
三、最長遞增子序列
1、問題
問題很好理解。例如:[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列,但它不是遞增的。
nums = [10,9,2,5,3,7,101,18] –> 4 [2,3,7,101] 或者 [2,3,7,18]
nums = [0,1,0,3,2,3] –> 4 [0,1,2,3]
nums = [7,7,7,7,7,7,7] –> 1 [7]
2、思想
定義:dp[i] 表示以 nums[i] 這個數結尾的最長遞增子序列的長度。為了理解這個定義,比如:dp[3] 就是以 nums[3] = 4 結尾的最長遞增子序列(1,3,4)的長度,也就是3。
根據這個定義,最終結果(子序列的最大長度)應該是 dp 數組中的最大值。

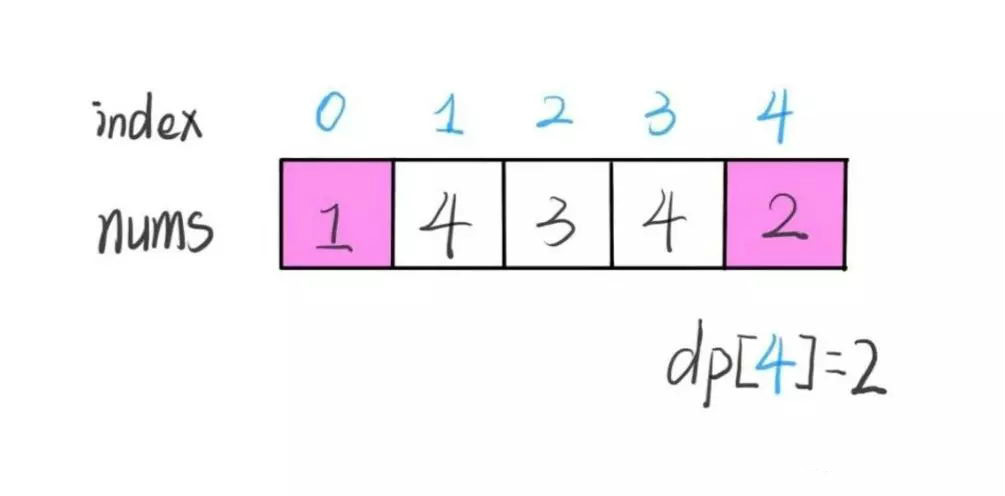
過程動圖

那麼,顯然有:
(1)邊界條件:dp[*] = 1
(2)動態轉移方程:dp[i] = nums[i] > nums[j] && max(dp[i], dp[j] + 1)
3、程式碼示例
1 // 時間複雜度 O(N^2) 2 public int lis(int[] nums) { 3 int[] dp = new int[nums.length]; 4 // dp數組全部初始化為 1 5 Arrays.fill(dp, 1); 6 7 for (int i = 0; i < nums.length; i++) { 8 for (int j = 0; j < i; j++) { 9 if (nums[i] > nums[j]) { 10 dp[i] = Math.max(dp[i], dp[j] + 1); 11 } 12 } 13 } 14 15 int res = 0; 16 for (int i : dp) { 17 res = Math.max(res, i); 18 } 19 20 return res; 21 }
四、最長迴文子串
1、問題
給定一個字元串 s,長度為 n,找到 s 中最長的迴文子串。
s = “abbac” –> “abba”
s = “cbbd” –> “bb”
s = “babad” –> “aba”
2、思想
定義:dp[i][j]表示 s 中 i 到 j 的字元串是否是迴文串。那麼,顯然有:
(1)邊界條件:dp[i][i] = true;dp[i][j] = true 當 s[i] = s[j] && j – i = 1
(2)狀態轉移方程:dp[i][j] = ( s[i] = s[j] && dp[i + 1][j – 1] )
3、程式碼示例
1 public int getLongestPalindrome(String s, int n) { 2 boolean[][] dp = new boolean[n][n]; 3 int max = 1; 4 5 // 字元串首尾字母長度差 (len = j - i) 0~n-1 6 for (int len = 0; len < n; len++) { 7 8 for (int i = 0; i < n - len; i++) { 9 int j = i + len; 10 11 // 如果字元串 i 到 j 的首尾相等,再根據字元串 i+1 到 j-1 來確定,即得到遞推公式 12 if (s.charAt(i) == s.charAt(j)) { 13 // 邊界條件 14 if (len == 0 || len == 1) { 15 dp[i][j] = true; 16 } else { 17 // 狀態轉移方程 18 dp[i][j] = dp[i + 1][j - 1]; 19 } 20 21 if (dp[i][j]) { 22 // 更新最大長度 23 max = Math.max(max, len + 1); 24 } 25 } 26 } 27 } 28 return max; 29 }
五、兌換硬幣
1、問題
給定一個正整數數組 coins,表示不同面值的硬幣,整數 amount 代表總金額。求可以湊成總金額所需的最少硬幣個數,不能組成總金額,返回 -1。硬幣數量無限。
coins = [1,3,5], amout = 11 -> 3(11 = 5 + 5 + 1)
coins = [2,5], amout = 3 -> -1
2、思想
用dp[i] = j 表示湊夠 i 元最少需要 j 個硬幣。先把問題規模縮小,考慮,如果有面值為1元、3元和5元的硬幣若干枚,如何用最少的硬幣湊夠11元?答案很簡單是 3(5+5+1)。則:
i = 0,表示湊夠0元最少需要的硬幣數。當然就是不選硬幣,需要0個硬幣。
dp[0] = 0
i = 1,只有1元可用,選擇 1 元硬幣,金額變為 i – 1 = 0,接下來只需要湊夠 0 元即可。
dp[1] = dp[i – 1] + 1 = dp[0] + 1 = 0 + 1 = 1
i = 2,只有1元可用,選擇 1 元硬幣,金額變為 i – 1 = 1,接下來只需要湊夠 1 元即可。
dp[2] = dp[i – 1] + 1 = dp[1] + 1 = 1 + 1 = 2
i = 3,可選硬幣有 1 和 3,則分兩種情況
①選擇 1 元硬幣,金額變為 i – 1 = 2,接下來只需要湊夠 2 元即可。
dp[3] = dp[i – 1] + 1 = dp[2] + 1 = 3 (3個1元的)
②選擇 3 元硬幣,金額變為 i – 3 = 0,接下來只需要湊夠 0 元即可。
dp[3] = dp[i – 3] + 1 = dp[0] + 1 = 1 (1個3元的)
顯然,上述情況取小:
dp[3] = min{dp[i – 1] + 1, dp[i – 3] + 1} = 1
i = 4~amount,同理可得。
歸納一下:在已知dp[0]、dp[1]、dp[2]、……dp[i – 1]求 dp[i] 時,在可取的硬幣面值(i >= coins[j],coins[j]表示第 j 個硬幣的面值),都取一次,則問題就可降級為 dp[i – coins[j]],而這個值是已知,最後取小即可。
案例說明:

不妨:coins = [1,3,5,20],求dp[11].
目的是湊成11,那麼,從可選的硬幣里選擇一枚,所有情況如下:
選擇coins[0]=1,則還需要湊11-1=10,即,在arr中湊10,所以dp[11]=dp[10] + 1。
選擇coins[1]=3,則還需要湊11-3=8,即,在arr中湊8,所以dp[11]=dp[11-3] + 1。
選擇coins[2]=5,則還需要湊11-5=6,即,在arr中湊6,所以dp[11]=dp[11-5] + 1。
注意:coins[3]=20 > 11,是不可選的。所以可選條件是 i >= coins[j]。
最後,在上述情況取小即可。
那麼,有:
(1)邊界條件:dp[0] = 0
(2)狀態轉移方程:dp[i] = min(dp[i], dp[i – coins[j]] + 1)。i – coins[j] >= 0
3、程式碼示例
1 // 兌換硬幣 2 public int minMoney(int[] coins, int amount) { 3 // 數組下標從 0 開始 4 int[] dp = new int[amount + 1]; 5 6 // 若最小硬幣是 1,那麼兌換 amount 最多用 amount 個硬幣。則 dp[amount] 最大等於 amount 7 // 由於下面要取小,所以給一個越界值 8 Arrays.fill(dp, amount + 1); 9 10 // 邊界條件 11 dp[0] = 0; 12 // 依次求dp[1]、dp[2]……dp[amount] 13 for (int i = 1; i < amount + 1; i++) { 14 15 // 遍歷硬幣的面值 16 for (int coin : coins) { 17 // 該硬幣面值可取 18 if (i - coin >= 0) { 19 dp[i] = Math.min(dp[i], dp[i - coin] + 1); 20 } 21 } 22 } 23 24 // 要是流程走下來 dp 值是非法值.說明換不出來 25 return dp[amount] == amount + 1 ? -1 : dp[amount]; 26 }
註:貪心不正確
coins = [1,4,5,7], amout=17
貪心結果:7+7+1+1+1 -> 5
實際:7+5+4+1 ->4
六、0-1背包問題
1、問題
一共有N件物品,第i(i從1開始)件物品的重量為w[i],價值為v[i]。在總重量不超過背包容量C的情況下,能夠裝入背包的最大價值是多少?
通俗的說,就是你有一個麻袋,你去超市順便拿東西,在不超出麻袋容量的情況下,儘可能的拿的物品價值和最大。
要求:①裝入背包的總價值最大,且重量不超出。②物品要麼拿,要麼不拿,不可重複拿。
2、思想
舉一個案例,有一個背包,容量為4kg,現有物品:
|
物品
|
重量
|
價值
|
|
吉他(G)
|
1kg
|
1500
|
|
音響(S)
|
4kg
|
3000
|
|
電腦(L)
|
3kg
|
2000
|
顯然:可取方案有G+L,價值3500;或S,價值3000。最佳方案:G+L,3500。
定義:dp[i][j]表示在前 i 個物品中選擇,能夠裝入容量為 j 的背包中的最大價值。即:
|
物品\重量
|
0kg
|
1kg
|
2kg
|
3kg
|
4kg
|
|
0
|
0
|
0
|
0
|
0
|
|
|
吉他(G)
|
0
|
||||
|
音響(S)
|
0
|
||||
|
電腦(L)
|
0
|
先把問題規模縮小,按一行一行(必須),背包容量為0、1、2、……C=4的順序,填寫上表。
表示物品只有吉他,有:
|
物品\重量
|
0kg
|
1kg
|
2kg
|
3kg
|
4kg
|
|
0
|
0
|
0
|
0
|
0
|
|
|
吉他(G)
|
0
|
1500
|
1500
|
1500
|
1500
|
|
音響(S)
|
0
|
||||
|
電腦(L)
|
0
|
表示物品有吉他、音響,有:
|
物品\重量
|
0kg
|
1kg
|
2kg
|
3kg
|
4kg
|
|
0
|
0
|
0
|
0
|
0
|
|
|
吉他(G)
|
0
|
1500
|
1500
|
1500
|
1500
|
|
音響(S)
|
0
|
1500
|
1500
|
1500
|
3000
|
|
電腦(L)
|
0
|
表示物品有吉他、音響、電腦,有:
|
物品\重量
|
0kg
|
1kg
|
2kg
|
3kg
|
4kg
|
|
0
|
0
|
0
|
0
|
0
|
|
|
吉他(G)
|
0
|
1500
|
1500
|
1500
|
1500
|
|
音響(S)
|
0
|
1500
|
1500
|
1500
|
3000
|
|
電腦(L)
|
0
|
1500
|
1500
|
2000
|
3500
|
那麼,有:
(1)邊界條件:dp[i][0] = dp[0][j] = 0。上表格第一列、第一行為0
(2)狀態轉移方程:dp[i][j] = max(dp[i – 1][j], v[i] + dp[i – 1][j – w[i]])
3、程式碼示例


1 public class Knapsack { 2 private Goods[] goods; 3 // 背包的容量 4 private int c; 5 // dp[i][j]:表示在前i個物品中選擇,能夠裝入容量為j的背包中的最大價值 6 private int[][] dp; 7 private int[][] path; 8 9 public Knapsack(Goods[] goods, int c) { 10 if (goods == null || goods.length == 0 || c <= 0) { 11 return; 12 } 13 this.goods = goods; 14 this.c = c; 15 16 this.dp = new int[goods.length][c + 1]; 17 this.path = new int[goods.length][c + 1]; 18 19 // 初始化第一列、第一行為0.可不寫,默認就是0 20 // for (int i = 0; i < dp.length; i++) { 21 // dp[i][0] = 0; 22 // } 23 // for (int i = 0; i < dp[0].length; i++) { 24 // dp[0][i] = 0; 25 // } 26 } 27 28 // 動態規劃 29 public void dp() { 30 for (int i = 1; i < dp.length; i++) { 31 for (int j = 1; j < dp[0].length; j++) { 32 // 表明當前物品放不了背包 33 if (goods[i].weight > j) { 34 dp[i][j] = dp[i - 1][j]; 35 } else { 36 dp[i][j] = Math.max(dp[i - 1][j], goods[i].value + dp[i - 1][j - goods[i].weight]); 37 38 // 用於記錄物品選擇策略 39 if (dp[i - 1][j] < goods[i].value + dp[i - 1][j - goods[i].weight]) { 40 path[i][j] = 1; 41 } 42 } 43 } 44 } 45 46 } 47 48 // 獲取物品的選擇策略 49 public List<Goods> getPlan() { 50 // 1.查看 dp 填寫情況 51 for (int i = 0; i < dp.length; i++) { 52 for (int j = 0; j < dp[i].length; j++) { 53 System.out.print(dp[i][j] + " "); 54 } 55 System.out.println(); 56 } 57 58 // 2.物品選擇策略 59 List<Goods> result = new ArrayList<>(); 60 int i = path.length - 1; 61 int j = path[0].length - 1; 62 // 從path的最後一個開始找 63 while (i > 0 && j > 0) { 64 if (path[i][j] == 1) { 65 result.add(goods[i]); 66 67 j = j - goods[i].weight; 68 } 69 i--; 70 } 71 return result; 72 } 73 } 74 75 // 物品 76 class Goods { 77 public String name; 78 // 物品重量 79 public int weight; 80 // 物品價值 81 public int value; 82 83 public Goods(String name, int weight, int value) { 84 this.name = name; 85 this.weight = weight; 86 this.value = value; 87 } 88 89 @Override 90 public String toString() { 91 return "Goods{" + 92 "name='" + name + '\'' + 93 ", weight=" + weight + 94 ", value=" + value + 95 '}'; 96 } 97 }
0-1背包


1 public class Main { 2 public static void main(String[] args) { 3 Goods[] goods = new Goods[4]; 4 5 // 為了使得 goods[1] 是第1個物品 6 goods[0] = null; 7 goods[1] = new Goods("吉他", 1, 1500); 8 goods[2] = new Goods("音響", 4, 3000); 9 goods[3] = new Goods("電腦", 3, 2000); 10 11 // 背包容量 12 final int C = 4; 13 Knapsack knapsack = new Knapsack(goods, C); 14 System.out.println("動態規劃dp:"); 15 knapsack.dp(); 16 17 final List<Goods> plan = knapsack.getPlan(); 18 System.out.println("物品選擇策略:"); 19 System.out.println(plan); 20 } 21 } 22 23 // 結果 24 動態規劃dp: 25 0 0 0 0 0 26 0 1500 1500 1500 1500 27 0 1500 1500 1500 3000 28 0 1500 1500 2000 3500 29 物品選擇策略: 30 [Goods{name='電腦', weight=3, value=2000}, Goods{name='吉他', weight=1, value=1500}]
測試類
4、說明
0-1背包問題不太好理解。下面用一些圖文幫助讀者理解。
首先,我們深刻理解一下0-1背包的問題,如圖:
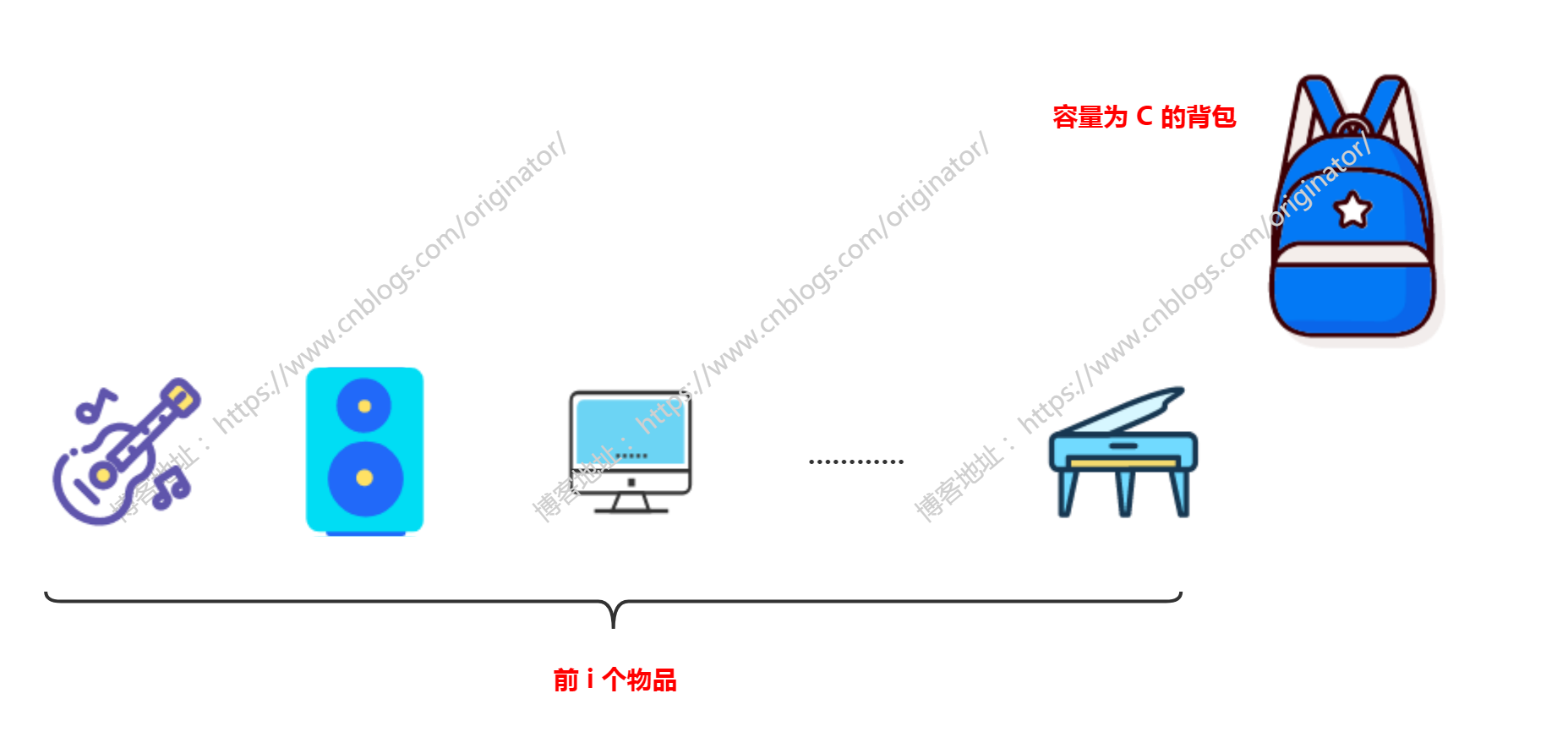
不妨假設,在這前 i 個物品中,選取總重量不超過背包容量 C 的物品,且使得物品總價值最大。選擇策略叫方案A,此時的最大總價值設為 maxValue。這裡理解一下前 i 個物品,由於動態規劃問題是規模逐漸增大的,所以,要姑且把物品看成是”有序的”。
那麼,我們思考一個問題,如果此時來了第 i + 1個物品(價值:V,重量:W),會怎麼樣呢?如圖:

主要分為兩種情況談論:
1、W > C :第 i + 1 個物品(鑽石)不可取。那麼,此時(總體物品是 i + 1個,但是)是不是就相當於沒有第 i + 1 這個物品(因為在i + 1個物品中選擇,不會取到第 i + 1這個物品),問題的解,是不是就等價於圖一(在 i 個物品中選擇,背包容量為C),所以,就是方案A,最大總價值就是 maxValue。
2、W <= C :第 i + 1個物品(鑽石)可取。又分為兩種情況:即拿或不拿。(註:這是0-1背包,一個物品要麼不選擇,要麼只選擇一次)
2.1:不拿。同樣,此時(這種情況下)問題的解,與上述(W > C)相同,即方案A,最大總價值就是 maxValue
2.2:拿。那麼,第 i + 1 個物品(鑽石)已經被選擇了,此時背包容量還有(C – W)。由於第 i + 1個物品已經被選擇了,此時問題規模,就是在前 i 個物品中,選取總重量不超過背包容量 C – W 的物品。價值就是dp[i][c – w]。
由於2.1和2.2屬於一種情況。所以整個問題的解就是 max( maxValue, V + dp[i][c – w] )。
下面,再對上面填表的過程,以及程式碼做一些解釋:


