統計學習：線性可分支援向量機(SVM)

• 2021 年 8 月 28 日
• 筆記
• 凸優化, 推導, 數學, 機器學習, 統計學習

模型

超平面

我們稱下面形式的集合為超平面

其中\(\bm{a} \in \mathbb{R}^n\)且\(\bm{a} \ne \bm{0} , \bm{x}\in \mathbb{R}^n, b \in \mathbb{R}\)。解析地看，超平面是關於\(\bm{x}\)的非平凡線性方程的解空間（因此是一個仿射集，仿射集和凸集的概念參考Stephen Boyd的《凸優化》）從幾何上看，它的的法向量為\(\bm{a}\)，而常數\(b\in \mathbb{R}\)決定了這個超平面從原點的偏移。這如何得到的呢？這是因為，若我們由法向量\(\bm{a}\)和超平面上一點\(\bm{x}_{0}\)確定超平面，則對超平面上任意一點\(\bm{x}\)，我們可以得到\(\bm{x} – \bm{x}_0\)一定垂直於\(\bm{a}\)，則超平面的集合便可以表示為

\(\mathbb{R}^2\)中的幾何化的解釋如下圖所示，其中深色箭頭表示\(\bm{x} – \bm{x}_0\)：
　

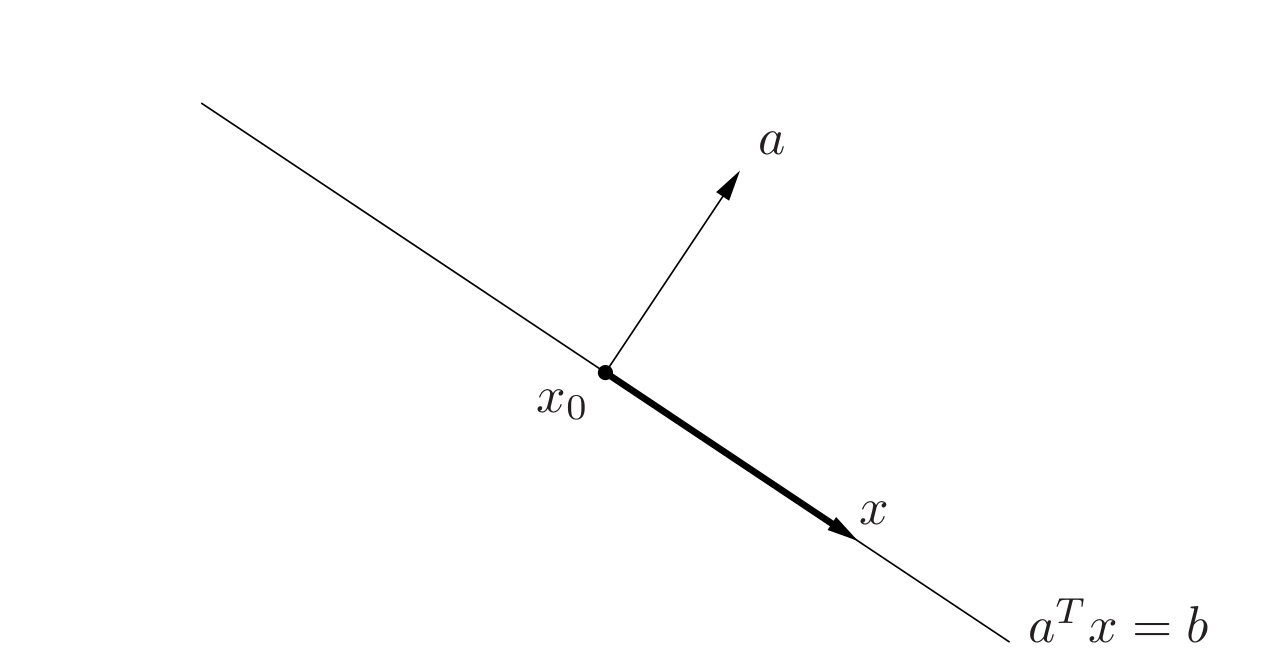
一個超平面將\(\mathbb{R}^n\)劃分為兩個半空間，（閉的）半空間是具有下列形式的集合：

即（非平凡）的線性不等式的解空間，其中\(a\ne 0\)。半空間是凸的，但不是仿射的。集合\(\{\bm{x} | \bm{a}^T \bm{x} -b < b\}\)是半空間\(\{\bm{x} | \bm{a}^T \bm{x} -b \leqslant 0\}\)的內部，稱為開半空間。

線性可分支援向量機

我們定義樣本空間為\(\mathcal{X} \subseteq \mathbb{R}^n\)，輸出空間為\(\mathcal{Y} = \{+1, -1\}\)。\(\bm{X}\)為輸入空間上的隨機向量，其取值為\(\bm{x}\)，滿足\(\bm{x} \in \mathcal{X}\)；\(Y\)為輸出空間上的隨機變數，設其取值為\(y\)，滿足\(y \in \mathcal{Y}\)。我們將容量為\(m\)的訓練樣本表示為:

當\(y^{(i)} = +1\)時，我們稱\(\bm{x}^{(i)}\)為正例；當\(y^{(i)} = -1\)時，稱\(\bm{x}^{i}\)為負例。\((\bm{x}^{(i)}, y^{(i)})\)稱為樣本點。
如果我們假設訓練數據集是線性可分的，則我們可以在特徵空間中找到一個分離超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0 \}\)，將特徵空間劃分為\(\{ \bm{x} | \bm{w}^T \bm{x} + b > 0 \}\)和\(\{ \bm{x} | \bm{w}^T \bm{x} + b < 0 \}\)兩個開半空間(顯然法向量\(\bm{w}\)指
向的一側為正，另一側為負)，且為正的一側對應負類，為負的一側對應負類。

如果訓練集線性可分，則我們存在無窮多個分離超平面將兩類樣本分開。如果我們採用感知機的誤分類最小的訓練策略(也就是僅僅保證分類的正確性)，那麼我們將求得無窮多個解。我們接下來定義的線性可分支援向量機將利用「間隔最大化」求解最優分離超平面（即能將兩組數據正確劃分且間隔最大的超平面，我們在「學習策略」板塊中將詳述這一概念），這時解是唯一的。

形式化地說，給定線性可分的數據集，通過間隔最大化策略學習得到的分離超平面為

稱為線性可分支援向量機。

學習策略

我們前面提到最好的超平面需要能將兩組數據正確劃分且間隔最大，那麼間隔最大如何形式化地定義呢？我們先來看函數間隔和幾何間隔的概念。

函數間隔和幾何間隔

直觀地看，一個點距離超平面的遠近可以表示則我們對它進行分類的確信程度。一個點距離超平面越遠，則我們對它的分類則越有把握。我們給定超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)和一個實例點\(\bm{x}^{(i)}\)，可以發現\(|\bm{w}^T \bm{x}^{(i)} + b|\)可以相對地表示點\(\bm{x}^{(i)}\)舉例超平面的遠近，而\(\bm{w}^T \bm{x}^{(i)} + b\)的符號與類標記\(y^{(i)}\)是否一致可以反映分類是否正確。據此，我們用\(y^{(i)} (\bm{w} \cdot \bm{x}^{(i)} + b)\)來對分類的確信度和正確性進行綜合表示。\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)為正數，表示分類器能夠正確完成分類功能，且\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)越大，則分類器越好；\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)為負數，就表示分類器連正確分類功能都不能完成了，負得越多，表示錯的越離譜(HaHa，應該可以這麼理解叭)。 於是，我們給出下列函數間隔的定義。

函數間隔 對於給定的數據集\(D\)和超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)，定義該超平面關於數據集中樣本點\((\bm{x}^{(i)}, y^{(i)})\)的函數間隔為

定義該超平面關於訓練集\(D\)的函數間隔為該超平面關於\(D\)中所有樣本點函數間隔的最小值，即

如果單單根據函數間隔的大小來選頂最佳超平面，那還不夠準確。因為我們知道，令超平面的法向量\(\bm{w}\)經過縮放變換為\(\lambda \bm{w}\)，超平面的截距項縮放變換為\(\lambda b\)，超平面是本身並沒有改變的，但函數間隔\(\hat{\gamma}^{(i)}\)卻變為\(\lambda \hat{\gamma}^{(i)}\)，這顯然與事實不符。因此，我們需要對超平面的法向量加一些約束，如規範化，令\(|| \bm{w} ||=1\)，使得間隔是確定的。這時的函數間隔就是我們後面所提到的幾何間隔的一種特殊情況。

我們定義實例\((\bm{x}^{(i)}, y^{(i)})\)到超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)的帶符號距離為\(\frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||}\)（在法向量那一側則為正），我們用這個做為來做為分類的確信度。類似地，我們我們用\(y^{(i)} \frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||}\)來對分類的確信度和正確性進行綜合表示。於是，我們給出下列幾何間隔的定義。

幾何間隔 對於給定的數據集\(D\)和超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)，定義該超平面關於數據集中樣本點\((\bm{x}^{(i)}, y^{(i)})\)的幾何間隔為

定義該超平面關於訓練集\(D\)的函數間隔為該超平面關於\(D\)中所有樣本點函數間隔的最小值，即

對比一下式\((7)、(8)\)和式\((9)、(10)\)我們知道，函數間隔和集合間隔存在下列關係\(\gamma^{(i)} = \frac{\hat{\gamma}^{(i)}}{||\bm{w}||}\)，\(\gamma = \frac{\hat{\gamma}}{||\bm{w}||}\)。可以看到，若\(||\bm{w}||=1\)，則函數間隔等於幾何間隔，如果\(\bm{w}\)和\(b\)都進行大小為\(\lambda\)的縮放變換，函數間隔也會縮放\(\lambda\)，但幾何間隔不變。

間隔最大化

要想使分離超平面更可靠，我們只需要保證該超平面關於\(D\)中所有樣本點幾何間隔的最小值\(\gamma\)盡量大即可（這樣自然就能保證所有點的幾何間隔盡量大)，我們稱此為間隔最大化策略（或稱為硬間隔最大化，和後面訓練集近似線性可分的軟間隔最大化相對應）。

可以知道，滿足間隔最大化的超平面是唯一的，它能夠對所有訓練數據有足夠大的確信度分類，也就是說不僅能夠對實例點進行分類，而且對於所有實例點能夠有足夠大的確信度分類，這樣的超平面的未知的測試實例有很好的分類預測能力。我們將該問題表述為以下帶約束優化問題：

根據\(\gamma = \frac{\hat{\gamma}}{||\bm{w}||}\)，我們可以將優化問題\((11)\)寫作：

我們將\(\bm{w}\)和\(b\)縮放變換為\(\lambda \bm{w}\)和\(\lambda b\)，則函數間隔\(\hat{\gamma}\)變為\(\lambda \hat{\gamma}\)。我們法線函數間隔的這一改變對\((11)\)中最優化問題的約束目標函數和不等式約束都沒有影響,也就是說它產生了一個等價的最優化問題。

這樣，就可以取\(\hat{\gamma}=1\)。將\(\hat{\gamma}=1\)代入上面的最優化問題，相當於最大化\(\frac{1}{||\bm{w}||}\)。不過這樣目標函數非凸，一般較難求解，為了將其轉換為凸優化問題，我們將原本的優化目標函數等價轉換為最小化\(\frac{1}{2}||\bm{w}||^2\)，這樣我們就將線性可分支援向量機的學習策略轉換為了一個(凸)二次規劃問題:

該形式稱為線性可分支援向量機的標準型。

附： 這裡提一下凸優化問題和二次規劃問題的概念。凸優化問題定義如下

其中目標函數\(f_0(\bm{x})\)和約束函數\(f_i(\bm{x})\)都為凸函數，且等式約束函數\(h_i(\bm{x})\)為仿射函數(也就是說，\(h_i(\bm{x})\)可以寫成\(h_i(\bm{x})= \bm{a}^T\bm{x} + b\)的形式。

特別地，當凸優化問題的目標函數\(f_0(\bm{x})\)是（凸）二次型並且約束函數\(f_i(\bm{x})\)為仿射時，該問題稱為二次規劃(QP)。二次規劃可以表述為：

其中\(\textbf{P}\)是對稱正定矩陣(在式\((13)\)中，\(\textbf{P}\)即是單位陣\(\textbf{I}\))，約束函數\(f_i(\bm{x})\)和等式約束函數\(h_i(\bm{x})\)都是仿射函數。

接下來我們會介紹該凸二次規劃問題的求解演算法。

演算法

接下來我們推導求解線性可分支援向量機的高效演算法。（真的是萬般皆推導，難的是演算法的推導過程，演算法實現反而很簡單）

直接求解式\((13)\)計算複雜度過高，而凸優化理論中告訴了我們許多可以高效求解\((13)\)問題的理論。我們將問題\((13)\)的形式做為原始問題(primal problem)。應用拉格朗日對偶性。通過求解對偶問題(dual problem)同樣得到原始問題的最優解，而且求解會更加高效。問題求解可分兩步走。
1. 推導原始問題的對偶形式並求得對偶問題的最優解\(\alpha^{*}\)。

我們引入拉格朗日乘子向量\(\bm{\alpha} = ( \alpha_{1}, \alpha_{2},…, \alpha_{m} )^T\)，每個不等式約束對應一個拉格朗日乘子\(\alpha_i \geq 0, i=1,2,…,m\)，我們以此定義拉格朗日函數：

（注意，標準凸優化問題式\((14)\)的約束項是小於等於，我們的式\((13)\)是大於等於，在寫出拉格朗日函數前，需要對原來的約束不等式兩邊同乘\(-1\)）

根據拉格朗日對偶性，原始問題的對偶問題是極大極小問題：

我們將問題拆解為先對\(\bm{w}\)、\(b\)求極小，再求對\(\bm{\alpha}\)求極大。

(1) 首先，我們求\(g(\bm{\alpha}) = \underset{\bm{w},b}{\min}L(\bm{w}, b, \bm{\alpha})\)。由凸函數\(L(\bm{w}, b, \bm{\alpha})\)極值滿足的一階必要條件有

可得：

關於\(\bm{w}\)的等式是一個對\(\bm{w}\)的顯式替換，而第二個等式是對式\(L(\bm{w}, b, \alpha)\)的一個約束，我們先將式\((19)\)中的等式一代入式\((16)\)的\(L(\bm{w}, b, \bm{\alpha})\)中有

雖然式\((19)\)沒有顯式的關於\(b\)的等式可供代入，但我們發現將第二個等式\(\sum_{i=1}^{m}\alpha_iy^{(i)}=0\)帶入後就可以將\(b\)的那項消掉，得到原問題的拉格朗日對偶函數(或對偶函數)為

可以看出，式\((22)\)這個對偶問題只用求解\(\bm{\alpha}\)係數而\(\bm{\alpha}\)係數只有支援向量才非0，其他全為0，這樣的話求解對偶問題的計算就會更加高效。至於求解式\((22)\)演算法的具體實現(一般採用內點法)可以調用凸優化庫Gurobi，在此不再詳述。
解式\((22)\)後我們得到\(\bm{\alpha}\)的解\(\bm{\alpha}^{*} = (\alpha_1^{*}, \alpha_2^{*}, …, \alpha_m^{*})^{T}\)。

2. 由對偶問題的最優解\(\alpha^{*}\)求得原始問題式\((13)\)的最優解\(\bm{w}^{*},b^{*}\)

如果\(\alpha^{*} = (\alpha_1^{*}, \alpha_2^{*}, …, \alpha_{m}^{*})^{T}\)是對偶最優化問題的解，我們將\(\alpha_i>0\)對應的實例點集合被稱為支援向量，我們設\(U = \{\alpha_i | \alpha_i >0 \}\)，我們\(U\)從中隨機采一個\(\alpha_s\)，對應的樣本為\((\bm{x}^{(s)}, y^{(s)})\)，可按下式求得原始最優化問題\((13)\)的解\(\bm{w}^{*}, b^*\)。

附： 式\((23)\)可根據KKT條件推導而得。KKT條件如下：

由式\((24)\)中第一個等式，我們可得：

其中至少有一個\(\alpha_i^{*}>0\)(用反證法，假設\(\alpha_i\)全為0，則\(\bm{w}^{*}\)為0，而易得\(\bm{w}\)為0不是原始問題\((13)\)的最優解，產生矛盾，故假設不符)。

式\((24)\)中第三個等式稱為KKT互補條件，我們設\(U = \{\alpha_i^* | \alpha_i^* >0 \}\)，我們\(U\)從中隨機采一個\(\alpha_s^*\)，對應的樣本為\((\bm{x}^{(s)}, y^{(s)})\)。因為有\(\alpha_s^*>0\)，則必有

我們將式\((25)\)代入式\((26)\)，方程兩邊同乘\(y^{(s)}\)，並注意到\(y^{(s)2}=1\)，我們有

(之所以寫成\(\langle \bm{x}^{(i)}, \bm{x} \rangle\)的內積形式是為了方便我們後面引入核函數)

給定測試樣本\(\bm{x}^*\)，我們就能按照式\((29)\)計算其類別\(f(\bm{x}^*)\)。由式\((23)\)可知，\(\bm{w}^*\)和\(b^*\)只依賴於\(\alpha_i>0\)的樣本點\((\bm{x}^{(i)}, y^{(i)})\)，而其他樣本點對\(\bm{w}^*\)和\(b\)沒有影響。我們將訓練數據中對應於\(a_i^*>0\)的實例點\(\bm{x}^{(i)} \in \mathbb{R}^n\)稱為支援向量。
綜上，按照式\((13)\)的策略求解線性可分支援向量機的演算法如下：　
　
觀察演算法的2、３步可知，我們只需要關注\(\alpha_i>0\)對應的相關的實例(也就是支援向量)，故實際計算複雜度其實很低。