演算法入門 – 基於動態數組的棧和隊列(Java版本)
之前我們學習了動態數組的實現,接下來我們用它來實現兩種數據結構——棧和隊列。首先,我們先來看一下棧。
什麼是棧?
棧是電腦的一種數據結構,它可以臨時存儲數據。那麼它跟數組有何區別呢?
我們知道,在數組中無論添加元素還是刪除元素,都可以根據索引位置或值進行操作,棧是否也支援這樣的操作呢?答案是不行,棧最大的特點就是後進先出(Last In First Out, LIFO):
棧雖然看似簡單,但是在電腦世界中有著非常重要的作用。比如在連續調用時,就利用了棧的特性:
public static void addNum(){
System.out.println("加法運算");
Scanner scanner = new Scanner(System.in);
System.out.print("請輸入整數a:");
int a = scanner.nextInt();
System.out.print("請輸入整數b:");
int b = scanner.nextInt();
System.out.println("a + b = " + (a + b));
}
public static void main(String[] args) {
addNum();
}
這裡,在調用 addNum 方法時,內部又依次調用了兩次 Scanner 實現輸入。所以可以這麼看,先調用了 addNum 方法,但是必須等待兩次 Scanner 調用完成後,addNum 方法才能結束:
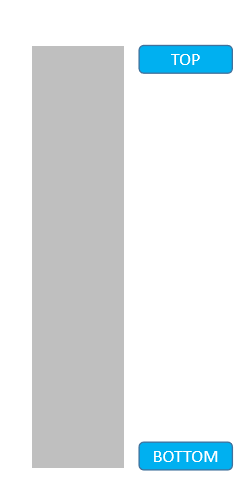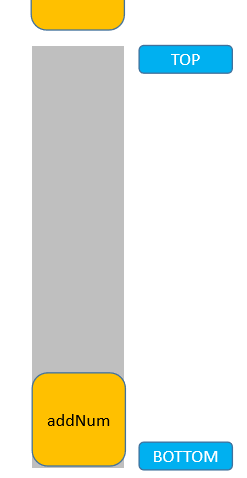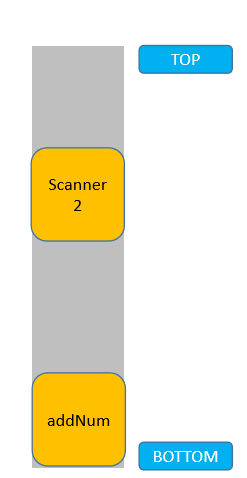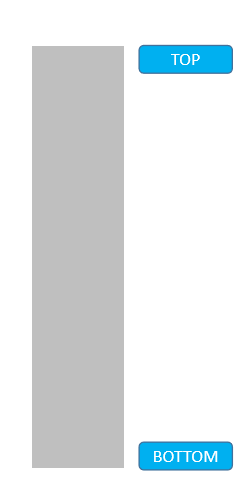
了解了棧後進先出的特點,我們就可以使用動態數組進行模擬了。
使用動態數組模擬棧
模擬的關鍵點在於「後進」和「先出」,也就是說,如果使用數組模擬的話,入棧時需要從數組尾部添加元素(addLast),出棧時也從尾部出棧(removeLast):
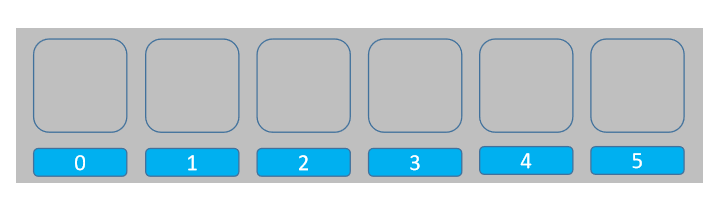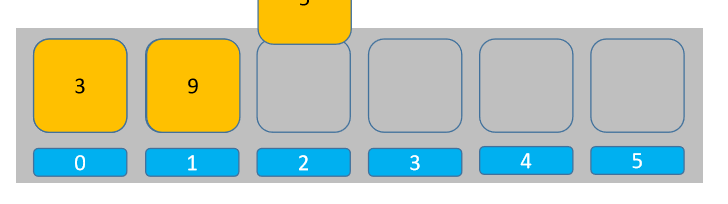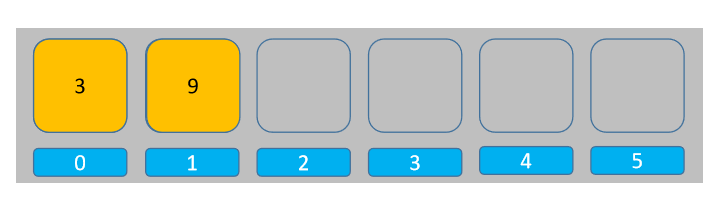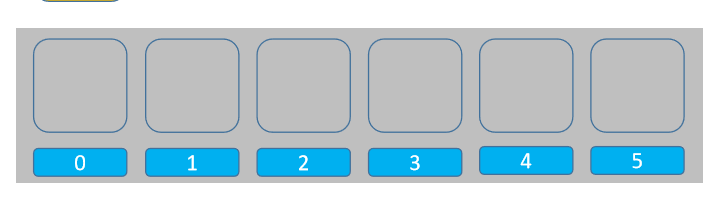
所以這樣一來,數組頭部實際上是棧底,數組尾部是棧頂。
接下來我們就用程式碼實現。
程式碼實現
首先定義棧的介面,規範棧的操作:
package com.algorithm.stack;
public interface Stack <E> {
void push(E element); // 入棧
E pop(); // 出棧
E peek(); // 查看棧頂元素
int getSize(); // 獲取棧長度
boolean isEmpty(); // 判斷棧是否為空
}
按照剛才說的,只要分別使用動態數組的 addLast() 和 removeLast() 方法替代棧的 push() 和 pop() 方法即可:
package com.algorithm.stack;
import com.algorithm.dynamicarrays.Array;
// 使用動態數組實現棧結構
// 棧底: index = 0; 棧頂: index = size - 1 (push: O(1), pop: O(1))
// 如果棧頂設在index=0的位置,push和pop都將面臨較大開銷(O(n))
public class ArrayStack<E> implements Stack<E>{
private Array<E> arr; // 使用之前實現的Array動態數組模擬棧
public ArrayStack(int capacity){
arr = new Array<>(capacity);
}
public ArrayStack(){
arr = new Array<>();
}
// 從棧頂壓入
@Override
public void push(E element){
arr.addLast(element);
}
// 從棧頂彈出
@Override
public E pop(){
return arr.removeLast();
}
// 從棧頂返回
@Override
public E peek(){
return arr.getLast();
}
// 棧長度
@Override
public int getSize(){
return arr.getSize();
}
// 棧容量
public int getCapacity(){
return arr.getCapacity();
}
// 判斷棧是否為空
@Override
public boolean isEmpty(){
return arr.isEmpty();
}
@Override
public String toString(){
StringBuilder str = new StringBuilder();
str.append(String.format("Stack: size = %d, capacity = %d\n[", getSize(), getCapacity()));
for (int i=0; i<getSize(); i++) {
str.append(arr.get(i));
if (i < getSize() - 1) {
str.append(", ");
}
}
str.append("] top"); // 標識出棧頂位置
return str.toString();
}
// main函數測試
public static void main(String[] args) {
ArrayStack<Integer> arrayStack = new ArrayStack<>();
for (int i =0; i<5; i++){
arrayStack.push(i);
System.out.println(arrayStack);
}
// pop
arrayStack.pop();
System.out.println(arrayStack);
}
}
/*
輸出結果:
Stack: size = 1, capacity = 10
[0] top
Stack: size = 2, capacity = 10
[0, 1] top
Stack: size = 3, capacity = 10
[0, 1, 2] top
Stack: size = 4, capacity = 10
[0, 1, 2, 3] top
Stack: size = 5, capacity = 10
[0, 1, 2, 3, 4] top
Stack: size = 4, capacity = 10
[0, 1, 2, 3] top
*/
結果符合預期。
棧的時間複雜度分析
入棧對應的數組操作是 addLast(),我們可以通過查看該方法的具體實現進行分析:
/**
* 在指定位置添加元素
* 指定位置處的元素需要向右側移動一個單位
* @param index 索引
* @param element 要添加的元素
*/
public void add(int index, E element) {
if (index < 0 || index > size) throw new IllegalArgumentException("Illegal index, index must > 0 and <= size!");
// 數組滿員觸發擴容
if (getSize() == getCapacity()) {
resize(2 * getCapacity()); // 擴容為原數組的2倍
}
// 從尾部開始,向右移動元素,直到index
for (int i = getSize() - 1; i >= index; i--) {
data[i + 1] = data[i];
}
// 添加元素
data[index] = element;
size++;
}
// 數組尾部添加元素
public void addLast(E element) {
add(getSize(), element);
}
/**
* 刪除指定位置元素
* 通過向左移動一位,覆蓋指定位置處的元素,實現刪除元素(data[size - 1] = null)
* @param index 索引
*/
public E remove(int index) {
if (index < 0 || index > size) throw new IllegalArgumentException("Illegal index, index must > 0 and < size!");
// 數組長度為0時拋出異常
if (getSize() == 0) throw new IllegalArgumentException("Empty array!");
E removedElement = data[index];
// 向左移動元素
for (int i = index; i < getSize() - 1; i++) {
data[i] = data[i + 1];
}
// 將尾部空閑出的位置置為空,釋放資源
data[getSize() - 1] = null;
size--;
// size過小觸發數組縮減
if (size == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2);
return removedElement;
}
// 刪除尾部元素
public E removeLast() {
return remove(getSize() - 1);
}
可以看出,每次從數組尾部添加元素時,add() 方法的 for 循環都無法滿足條件,等同於直接在 size 處添加元素,所以時間複雜度為 O(1)。如果再考慮數組滿員後觸發的 resize 操作,相當於是進行了 n+1 次 add() 操作後才會觸發 n次操作的 resize(移動n個元素至新數組),所以每次 add() 操作平均耗時為 \(\frac{2n+1}{n+1} \approx 2\),是一個與數組長度 n 無關的數,所以也可以看做是 O(1) 複雜度的。
同理,出棧對應的 removeLast() 的時間複雜度也是 O(1)。
什麼是隊列?
理解了棧後,隊列就更簡單了。實際上,隊列是我們日常生活中幾乎每天都會碰到的。我們去超市買東西結賬時需要排隊,去銀行辦理業務時需要排隊,做核酸、打疫苗就更需要排隊了😂:

所以隊列是一種先進先出的數據結構。
使用動態數組模擬隊列
如果將隊列也轉換成數組,會是這樣:

可以看出,入隊的操作與入棧的實現方式相同,而出隊則是從數組頭部(removeFirst)。
程式碼實現
同樣,我們先定義隊列介面:
package com.algorithm.queue;
public interface Queue<E> {
void enqueue(E element); // 入隊
E dequeue(); // 出隊
E getFront(); // 獲取隊首元素
int getSize(); // 獲取隊列長度
boolean isEmpty(); // 判斷隊列是否為空
}
package com.algorithm.queue;
import com.algorithm.dynamicarrays.Array;
// 使用動態數組實現隊列
public class ArrayQueue<E> implements Queue<E>{
private Array<E> arr; // 使用之前實現的Array動態數組模擬隊列
public ArrayQueue(int capacity){
arr = new Array<>(capacity);
}
public ArrayQueue(){
arr = new Array<>();
}
// 隊首: index = 0; 隊尾: index = size - 1
// 隊尾入隊
@Override
public void enqueue(E element){
arr.addLast(element);
}
//隊首出隊
@Override
public E dequeue(){
return arr.removeFirst();
}
// 隊首返回
@Override
public E getFront(){
return arr.getFirst();
}
// 隊列長度
@Override
public int getSize(){
return arr.getSize();
}
// 判斷隊列是否為空
@Override
public boolean isEmpty(){
return arr.isEmpty();
}
// 隊列容量
public int getCapacity(){
return arr.getCapacity();
}
@Override
public String toString(){
StringBuilder str = new StringBuilder();
str.append(String.format("Queue: size = %d, capacity: %d\ntop [", getSize(), getCapacity()));
for (int i=0; i< getSize(); i++) {
str.append(arr.get(i));
if (i< getSize() - 1) {
str.append(", ");
}
}
str.append("] tail"); // 標識隊尾
return str.toString();
}
// main函數測試
public static void main(String[] args) {
ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
for (int i=0;i<5;i++){
arrayQueue.enqueue(i);
System.out.println(arrayQueue);
if (i % 3 == 2){ // 每隔3個元素進行出隊操作
arrayQueue.dequeue();
System.out.println(arrayQueue);
}
}
}
}
/*
輸出結果:
Queue: size = 1, capacity: 10
top [0] tail
Queue: size = 2, capacity: 10
top [0, 1] tail
Queue: size = 3, capacity: 10
top [0, 1, 2] tail
Queue: size = 2, capacity: 5
top [1, 2] tail
Queue: size = 3, capacity: 5
top [1, 2, 3] tail
Queue: size = 4, capacity: 5
top [1, 2, 3, 4] tail
*/
隊列的時間複雜度分析
入隊的時間複雜度與之前入棧相同,都是 O(1);而出隊由於是從數組頭部出,所以會觸發剩餘元素向左移動,所以時間複雜度為 O(n)。
總結
通過對動態數組的學習,並實現了棧和隊列兩種比較基礎的數據結構,讓我們能夠更深入的了解這些結構背後的原理,為我們今後學習更複雜的數據結構打下基礎。
