樹狀數組基礎
樹狀數組簡介
如果有哪一種數據結構可以支援區間/單點和的更新和查詢,一個顯而易見的答案就是萬能的線段樹。但是線段樹雖然能支援很多的區間問題,但是程式碼量有些長。如果我們只是單純地為了維護區間和其實並不用去專門構建一棵線段樹。樹狀數組作為一種更加簡單的,可以維護區間和的數據結構應運而生。
樹狀數組基本思想
對於數組\(A\)來說,如果我們要求Sum(Ai , Aj)的結果,除了使用直接遍歷或者是線段樹,我們還可以為其定義一個數組\(C\)像下面這樣:
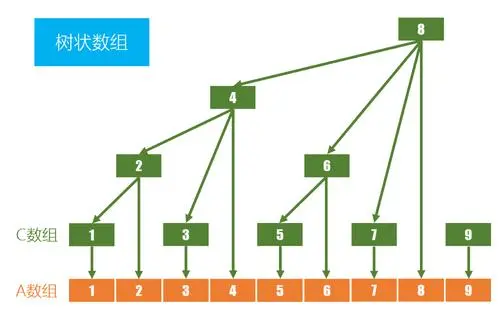
然後我們可以簡單地羅列一個c數組到a數組到映射關係
| A數組 | C數組 |
|---|---|
| A1 | A1 |
| A2 | A1+A2 |
| A3 | A3 |
| A4 | A1+A2+A3+A4 |
| A5 | A5 |
| A6 | A5+A6 |
| A7 | A7 |
| A8 | A1+A2+A3+A4+A5+A6+A7+A8 |
| A9 | A9 |
我們可以把c數組看成一種特殊的前綴和。一般的前綴和的\(s~i~\)都是代表著\(A~i-A~0\) 的值,但是我們的c數組每一位代表著的值是像上面這個表寫著的那樣。
那麼剩下的任務就是找規律了。最先可以看到的是對於\(A~i~\)來說,如果i是奇數的話,那麼有\(C~i~ = A~i~\)。如果i是偶數的話,我們可以發現這樣一條規律:設x為 i 的二進位形式中最低位1所代表的值,有\(C~i~ = Sum(A~x~ , A~1~)\) 。求出x值的函數我們一般稱之為lowbit()函數,寫法如下:
def lowbit(a):
return a&(-a)
這樣我們就可以完成C數組的維護。假設我們要在保持c數組維護著前綴和的性質的前提下更改A[1]的值(A[1]=A[1]+x),可以按照這樣的順序對C數組進行修改:
C[1]=C[1]+x lowbit(1)==1
C[2]=C[2]+x 1+lowbit(1)==2
C[4]=C[4]+x 2+lowbit(2)==4
C[8]=C[8]+x 4+lowbit(4)==8
寫成程式碼就是這樣:
def add(x,pos):
while pos<=n:
C[pos]+=x
pos=pos+lowbit(pos)
區間查詢的思想和單點更新其實差不多(就是單點更新的反向操作),看看程式碼就能理解了:
def query(pos):
ans=0
while(pos>0):
ans+=tree[pos]
pos=pos-lowbit(pos)
return ans
樹狀數組在逆序對上的應用
逆序對問題除了可以通過歸併排序進行合併以外還可以用樹狀數組進行計算
逆序對問題就是求對於數組\(A\)來說,存在一組i,j使得i<j且\(A~i~>A~j~\) 我們稱i,j為一組逆序對。逆序對問題通常是用歸併排序的方式來分治計算,同時也可以用樹狀數組來計算
可以簡單地把逆序對問題看成計算對於每一個數字,它前面有多少個比它大的數字,最後的答案就是對於每個數字的結果的和。首先,我們對輸入數據進行離散化,因為輸入數據大小可能會很大。然後,我們用離散化之後的數據下標構建一個全0樹狀數組。對於一個數,所有比它大的數字都可以通過計算下標數組上在他前面的數字的個數。此時就可以通過樹狀數組來加速計算的過程。
其實用線段樹也可以進行計算,不過從程式碼量上來說還是樹狀數組更優一些。
樹狀數組可以被看作一種用來維護結合律支援的區間操作的一種程式碼量和細節都比較少的數據結構。如果要維護某些不支援結合律(比如說區間眾數)之類的值的時候還是好好地打線段樹吧

