【數據結構與演算法】字元串匹配(後綴數組)
概念
簡介
在電腦科學裡, 後綴數組(英語:suffix array)是一個通過對字元串的所有後綴經過排序後得到的數組。此數據結構被運用於全文索引、數據壓縮演算法、以及生物資訊學。
後綴字元串
- 後綴字元串:從後往前依次遞增截取的字元串。長度為 n 的字元串有 n 個後綴
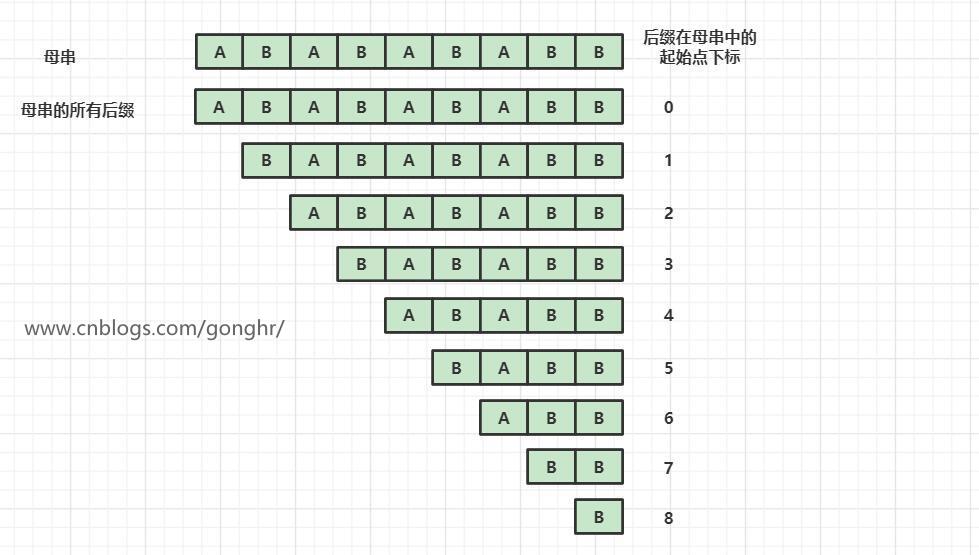
後綴數組和rank數組
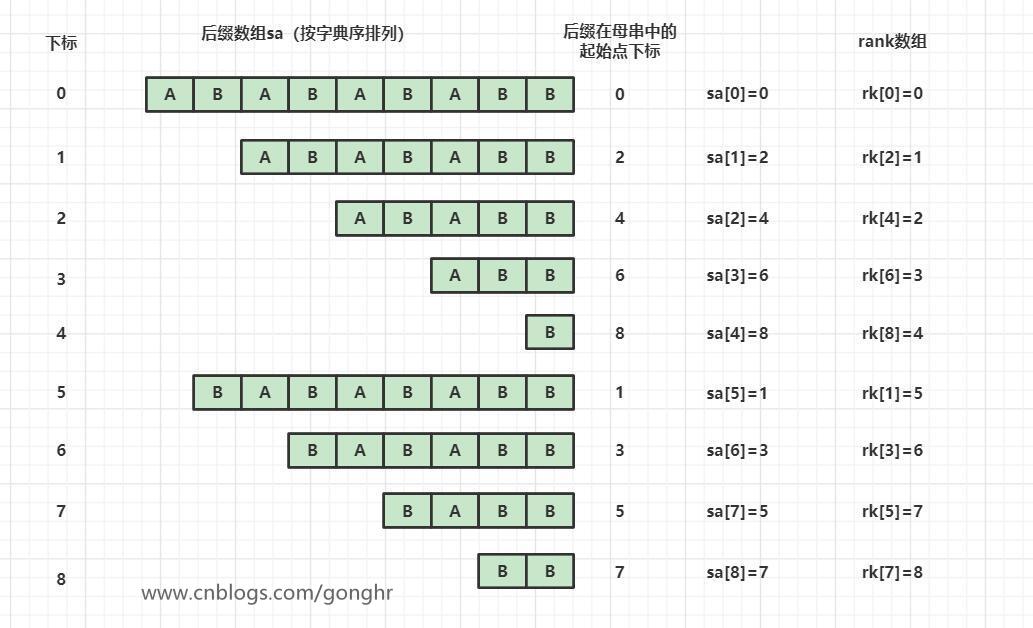
-
後綴數組:排名和原下標的映射。把字元串的n個後綴子串按照字典序從小到大排列,形成的數組,在數組中記錄後綴的起始下標。是排名到下標的映射。
sa[m]=n表示排名是m的後綴字元串在原字元串的起點是n如:sa[0]=5 表示排名是0位的後綴字元串在原字元串的起點是5
-
rank數組:給定後綴的下標,返回其字典序。是下標到排名的映射。
rk[n]=m表示後綴在原字元串起點是n的字元串的排名是m如:rk[5]=0 表示後綴在原字元串起點是5的字元串排名為0位
-
顯然,後綴數組和rank數組是互補的
sa[rk[i]] = rk[sa[i]] = i
思路分析
後綴數組主要用於字元串匹配的查詢。
有一個顯而易見的基本概念:字元串的子串一定是某個後綴的前綴
如果給定一個字元串,想看它是不是母串的子串,那麼我們可以先構造母串的後綴數組,然後使用二分查找,根據字典序查找出與該字元串最匹配的後綴,然後遍歷後綴,如果該字元串是該後綴的前綴,那麼就說明該字元串是母串的子串;否則不是。
如何求後綴數組以及進行字元串匹配
樸素法
獲取所有後綴放入數組,然後使用Arrays.sort() 按照字典序排序。
注意:不僅要獲取後綴,後綴在母串的起點下標也需要獲取,也就是說後綴和其在母串的起點下標是一體,不可分割的,為了解決這個問題,需要把後綴字元串和其起點下標封裝成對象,並且實現Comparable介面。
//求後綴數組
public static Suff[] getSa(String src) {
int strLength = src.length();
/*sa是排名到下標的映射,即sa[i]=k說明排名為i的後綴是從k開始的*/
Suff[] suffixArray = new Suff[strLength];
for (int i = 0; i < strLength; i++) {
String suffI = src.substring(i);//截取後綴
suffixArray[i] = new Suff(i, suffI);
}
Arrays.sort(suffixArray);//依據Suff的比較規則進行排序
return suffixArray;
}
//封裝後綴和起點下標
class Suff implements Comparable<Suff> {
String str; //後綴內容
int index;//後綴的起始下標
public Suff(int index, String str) {
this.index = index;
this.str = str;
}
@Override
public int compareTo(Suff o2) {
return this.str.compareTo(o2.str);
}
@Override
public String toString() {
return "Suff{" +
"str='" + str + '\'' +
", index=" + index +
'}';
}
}
- 時間複雜度:快排
O(nlogn),字元串一一匹配還需乘O(n),所以總的時間複雜度是O(n^2·logn)
倍增法
倍增演算法的主要思路是:用倍增的方法對每個字元開始的長度為2^k的子字元串進行排序,求出排名,即rank值。k 從О開始,每次加1,當2^k大於n以後,每個字元開始的長度為2^k的子字元串便相當於所有的後綴。並且這些子字元串都一定已經比較出大小,即rank值中沒有相同的值,那麼此時的rank值就是最後的結果。每一次排序都利用上次長度為2^(k-1)的字元串的rank值,那麼長度為2^k的字元串就可以用兩個長度為2^(k-1)的字元串的排名作為關鍵字表示,然後進行快速排序,便得出了長度為2^k的字元串的rank值。
這裡和羅穗騫論文里的排序思路略有不同,採用快速排序簡化程式碼幫助理解。

用rank數組記錄sa數組中每個index的排名。
修改一下Suff類:
class Suff implements Comparable<Suff> {
public char c;//後綴內容
private String src;
public int index;//後綴的起始下標
public Suff(char c, int index, String src) {
this.c = c;
this.index = index;
this.src = src;
}
@Override
public int compareTo(Suff o2) {
return this.c - o2.c;
}
@Override
public String toString() {
return "Suff{" +
"char='" + src.substring(index) + '\'' +
", index=" + index +
'}';
}
}
改進的求後綴數組方法:
public static Suff[] getSa(String src) {
int n = src.length();
Suff[] sa = new Suff[n];
for (int i = 0; i < n; i++) {
sa[i] = new Suff(src.charAt(i), i, src);//存單個字元,接下來排序
}
Arrays.sort(sa); //單個字元使用快排
/*rk是下標到排名的映射*/
int[] rk = new int[n]; //rank數組
rk[sa[0].index] = 1; //排名從1開始
for (int i = 1; i < n; i++) {
rk[sa[i].index] = rk[sa[i - 1].index]; //下標所指字元相同則排名相同
if (sa[i].c != sa[i - 1].c) rk[sa[i].index]++; //字元不同,則排名加一
}
//倍增法
for (int k = 2; rk[sa[n - 1].index] < n; k *= 2) { //外層O(logn)
final int kk = k;
Arrays.sort(sa, (o1, o2) -> {
//不是基於字元串比較,而是利用之前的rank
int i = o1.index;
int j = o2.index;
if (rk[i] == rk[j]) {//如果第一關鍵字相同
if (i + kk / 2 >= n || j + kk / 2 >= n)
return -(i - j); //如果某個後綴不具有第二關鍵字,那肯定較小,索引靠後的更小
return rk[i + kk / 2] - rk[j + kk / 2];
} else {
return rk[i] - rk[j];
}
});
/*---排序 end---*/
// 更新rank
rk[sa[0].index] = 1;
for (int i = 1; i < n; i++) {
int i1 = sa[i].index;
int i2 = sa[i - 1].index;
rk[i1] = rk[i2];
try { //兩個字元串不相同,排名加一
if (!src.substring(i1, i1 + kk).equals(src.substring(i2, i2 + kk)))
rk[i1]++;
} catch (Exception e) { //i1+kk越界了,則說明i1字元串比i2字元串短,且原先排名在i2之後,所以排名加一
rk[i1]++;
}
}
}
return sa;
}
- 時間複雜度:快排複雜度
O(nlogn),外層循環logn層,所以總的時間複雜度是O(n(logn)^2)
更好的優化
內部字元串比較的時候使用基數排序O(n)可以時總的時間複雜度降低到O(nlogn)
還有時間複雜度為O(n)級別的DC3和SA-IS方法,可自行查閱資料,已放在文末。
二分法匹配字元串
private static void match(String s, String p) { //s是母串,p是模式串
Suff[] sa = getSa(s); //獲取後綴數組
int l = 0;
int r = s.length() - 1;
//二分查找,nlog(m)
while (r >= l) {
int mid = l + ((r - l) >> 1);
//居中的後綴
Suff midSuff = sa[mid];
String suffStr = s.substring(midSuff.index); //獲取後綴
int compareRes;
//將後綴和模式串比較,O(n)
if (suffStr.length() >= p.length()) //後綴字元串長度大於等於模式串,截取後綴字元串的前綴與模式串比較
compareRes = suffStr.substring(0, p.length()).compareTo(p);
else //後綴字元串長度小於模式串,直接進行比較
compareRes = suffStr.compareTo(p);
//相等了,輸出後綴的起始位置
if (compareRes == 0) {
System.out.println(midSuff.index);
break;
} else if (compareRes < 0) { //後綴小於模式串,左指針右移
l = mid + 1;
} else { //後綴大於模式串,右指針左移
r = mid - 1;
}
}
}
高度數組
概念
-
高度數組:(height)是後綴數組中每兩個相鄰字元串元素的最長公共前綴的長度的集合
-
LCP:(longestCommonSubString)最長公共前綴
-
height[i] = LCP(sa[i],sa[i-1])
思路和實現
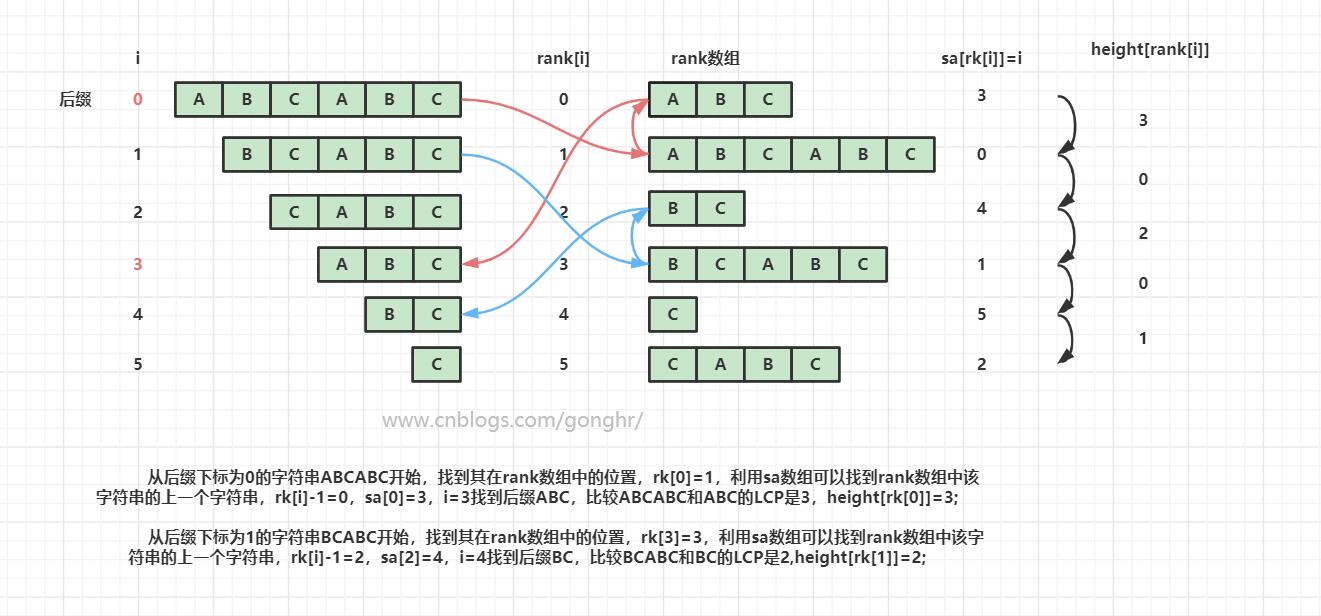
如果已經知道後綴數組中i與i+1的lcp為h,那麼i代表的字元串與i+1代表的字元串去掉首字母后的lcp為h-1.
根據這個我們可以發現,如果知道i與後綴數組中在它後一個的lcp為k,那麼它去掉首字母后的字元串與其在後綴數組中的後一個的lcp大於等於k-1.
即height[rk(i+1)] >= height[rk(i)]-1
例如對於字元串abcefabc,我們知道abcefabc與abc的lcp為3.
那麼bcefabc與bc的lcp大於等於3-1.
利用這一點就可以O(n)求出高度數組。
public static int[] getHeight(String src, Suff[] sa) {
int strLength = src.length();
int[] rk = new int[strLength];
//將rank表示為不重複的排名即0~n-1
for (int i = 0; i < strLength; i++) {
rk[sa[i].index] = i;
}
int[] height = new int[strLength];
int k = 0;
for (int i = 0; i < strLength; i++) {
int rk_i = rk[i]; //i後綴的排名
if (rk_i == 0) {
height[0] = 0;
continue;
}
int rk_i_1 = rk_i - 1;
int j = sa[rk_i_1].index;//j是i串字典序靠前的串的下標
if (k > 0) k--;
for (; j + k < strLength && i + k < strLength; k++) {
if (src.charAt(j + k) != src.charAt(i + k))
break;
}
height[rk_i] = k;
}
return height;
}

