【乾貨】一份小白前端可視化學習指南——附思維導圖

前言

因為群里粉絲一直要求我寫一篇可視化入門指南，今天他來了。其實說起前端可視化，大家所能想到的就是各種圖表，大屏。這種看著賊炫酷，而筆者呢工作也一直從事3D前端開發工作，慢慢對圖形產生了興趣。但是呢一直做的是三維的東西，沒搞過二維的。大概是2月前開始學習2D的一些東西，然後並寫了一些文章，效果還不錯。所以我就寫一些經驗之談，大佬勿噴。 我大概從4個方面去講我是怎麼學習的

  1. 可視化不得不掌握的數學基礎

  2. svg方面的學習

  3. canvas方面的學習

  4. 可視化中不得不掌握的圖形演算法

讀完本篇文章，你可以大概知道我該怎麼去學，需要學什麼？以及我推薦的一些學習資料和學習資源！

數學篇

提起數學很多程式設計師頭疼哇，我寫程式碼還要學可惡的數學，但是我很明確的告訴你——很重要，如果你想學可可視化的話，數學很重要，背後的幾何意義更重要。讀者一開始理解不深，導致很多東西理解不了，吃了很多虧哇！

向量

在二維空間或者三維空間中， 是不是都有點的概念，只不過一個是二維的一個是三維的， 假設，現在這個平面直角坐標繫上有一個向量 v。向量 v 有兩個含義：一是可以表示該坐標系下位於 (x, y) 處的一個點；二是可以表示從原點 (0,0) 到坐標 (x,y) 的一根線段。

向量

我在寫canvas的同時就喜歡用一個Point2d 類就是這個原理， canvas本身就是坐標系。畫布上的點都可以用向量表示， 原點在左上方。

向量加減法

一個向量可以用其他兩個向量去表示，也可以用兩個向量去做減法，我說個實際工作中經常用到的例子： 如何讓一個點在某一個方向延展多少長度呢？

這裡其實就是用到了向量的加法， 首先這個方向肯定是是個單位向量 ， 為什麼是單位向量呢？？ 因為向量是有大小和方向的， 而單位向量 只有方向， 長度 為1 ，然後我們只要開始點 加上 這個方向向量 ✖️ 長度。就可以得到了。 背後不就是向量加法的運用。 我還是畫圖給大家展示下吧。

向量加法

如圖：我要從A-B點 方向是od 然後你可以乘以任何長度 得到 OD 然後相加， 是不是就可以得到B點了。 一圖勝千言！，減法大家可以自己去思考，同樣的道理的

向量的叉乘和點乘

其實很多種實踐，這裡我就舉一個例子哈，帶你了解點乘。其實還有投影

向量點乘可以用來判斷 連個向量是否同一方向， 我還是畫圖給大家講解， 不說太多理論，都是實戰中經常用到的。

叉乘

A向量和B向量之間的夾角是銳角 所以是同向 ， B向量和C量之間的夾角是鈍角所以是反向 ，因為點乘的數學公式就是兩個向量的模長 × cosθ 。

叉乘

叉乘的幾何意義也是非常重要的，可以算多邊形的面積， 計算出另一個向量 垂直於這兩個向量。 還是開始畫圖：

垂直

X向量 和 Y向量去做叉乘 得到的 向量Z 是 xy 平面的normal。

算面積：

面積

叉乘的數學意義： A向量的模長 × B向量的模長 × sinθ 不就是平行四邊形的高 H 所以可以用來算面積。

叉乘還可以用來判斷三個點的方向

Corss 的幾何叉積得到的是一個數值， 只要判斷當前數值是大於0 小於 0就好了， 就知道這個三個點的方式是逆時針 還是順時針就好了。

順時針還是逆時針

圖中可以看到 OAB 和OA1B 的方向是不同，OA向量✖️ OB向量 的值 和 OA1 ✖️OB向量 算出的來的值 是相反的。公式我給大家列舉下：

a.x * b.y – a.y * b.x

其實向量的點乘 和叉乘非常的重要，大家一定要要好理解，後面的圖形演算法，很多也是基於這個去實現的。

矩陣

空間中圖形的大部分變化都是可以通過矩陣去表示的，大概有下面幾種類型：

  1. 平移矩陣
  2. 旋轉矩陣
  3. 縮放矩陣
  4. 鏡像矩陣
  5. 錯切矩陣
  6. 投影矩陣

這裡我給大家推薦的學習資源是B站的：

//www.bilibili.com/video/BV1ib411t7YR?from=search&seid=15308763710996235630

線性代數的本質，看完你就能夠明白了，包括上面的向量之間的變化。

鏡像矩陣我推薦你看我這篇文章， 我是求導了三維空間中任意平面的鏡像矩陣的了，

求空間任意平面的鏡像矩陣

我這裡給大家簡單的講解下最簡單的變化—— 平移矩陣

還是看下圖吧:

平移矩陣

在這樣的三維坐標系中從A點平移到B點 x變化了 2 y變化了0 z 變化了 2 對應矩陣的寫法是什麼呢：
$$
\begin{bmatrix}
1&0&0&2\
0&1&0&0\
0&0&1&2\
0&0&0&1\
\end{bmatrix}
×
\begin{bmatrix}
2\
0\
4\
1\
\end{bmatrix}

=

\begin{bmatrix}
4\
0\
6\
1\
\end{bmatrix}
$$

其實矩陣中每一行都有對應的矩陣， 平移矩陣一般改變的第四列的前三個數字

曲線

無論是2d還是3d都需要曲線的表達，最簡單的圓弧、橢圓弧、然後連續曲線可以用貝塞爾曲線去表達，還有B樣條曲線，nurbs曲線。掌握曲線最終的還是數學哇。

圓的方程： x ^2 + y ^ 2 = r ^ 2

橢圓的方程： x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1

n階貝塞爾曲線的方程： 𝐵(𝑡)=∑𝑖=0𝑛𝑃𝑖(1−𝑡)𝑛−𝑖𝑡𝑖,𝑡𝜖[0,1]

b樣條曲線和nurbs曲線我還沒接觸過，但是我們組的小夥伴正在做自由曲面，可能涉及到了。這裡我只是簡單表示了直線方程，有了方程你可以你去進行高度模擬，比如我在做3D文字的時候，我們底層演算法庫還沒有支援貝塞爾， 不過沒關係我們不是有方程嘛， 可以通過方程將貝塞爾曲線離散成多個點，然後用直線去表達。因為我們人眼去看螢幕上的東西，離散的很多的話，肉眼是完全看不出來的。 我這裡給大家看一張圖吧：

弧線

圗這個部分的弧線我就是用我貝塞爾曲線 離散成直線去表達的， 還有國中的點其實也是貝塞爾曲線離散成直線去做的。從視覺上來看是能夠近似模擬的。3D文字中的 更多技術，我後面會專門寫一篇文章去詳細介紹， 順便自己去梳理下。如果你感興趣，那你可得關注我，不然就找不到我了。

坐標系的轉換

為什麼要有這個東西呢，canvas和svg的坐標系都是左上方是原點，這一點你不覺得有點反人類？ 好不舒服，我在畫折線圖的時候就發現了，從原點向上，坐標軸是遞減的。其實這個問題怎麼解決呢，其實很簡單就是我們進行坐標系的轉換，我將原先畫布的原點， 通過變化到左下角， 這樣我們在計算點的坐標的時候，就沒有心智負擔了，該怎樣就是怎樣。 說完2d我再和你聊聊3D， 就拿Three.js 舉例子吧有個局部坐標系，觀察坐標系（相機）、 世界坐標系、裁剪坐標系、螢幕坐標系。

這是空間中某個物體到最終螢幕所做的一系列操作。

  1. 首先物體的自身有個坐標系我們叫做局部坐標系，他也有個原點，但是他在世界坐標系下也有對應的位置，所以他們之間有一個矩陣變化——模型矩陣

  2. 世界坐標系——到觀察坐標系也有矩陣變化， 這叫視圖矩陣

  3. 觀察空間——裁剪空間 叫做 投影矩陣因為3維空間的東西我們是用相機去模擬人眼，在視椎體內的東西才能被看到。所有就有了投影矩陣， 有透視投影和正交投影， 一個近大遠小，一個遠近都是一樣的

  4. 標準設備坐標-螢幕坐標。 這裡就涉及到坐標系的原點的問題。

    坐標系

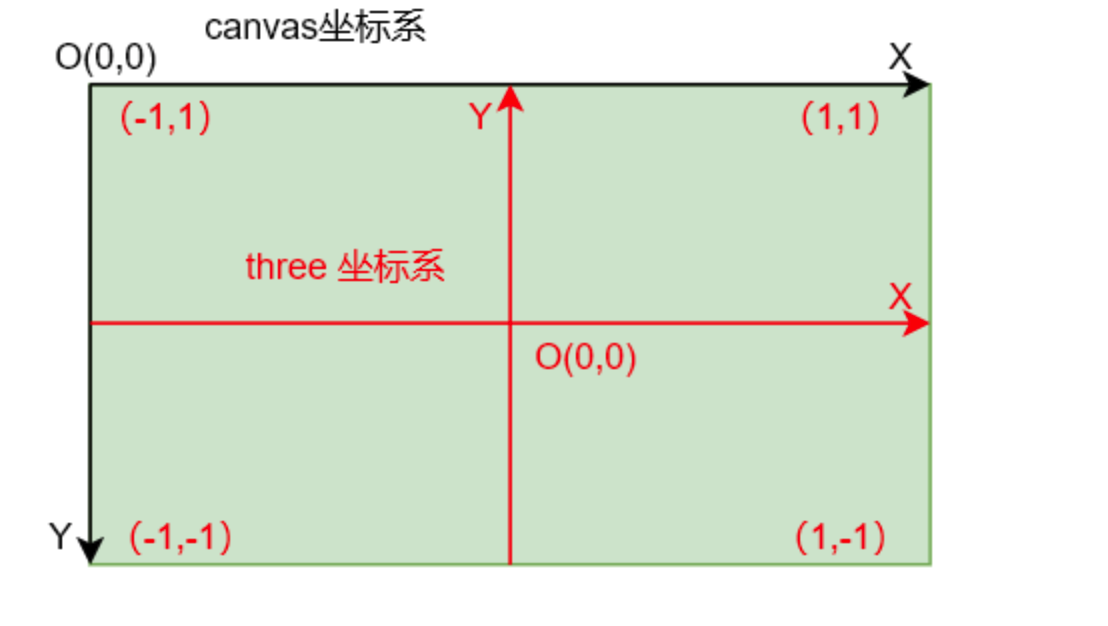
歸一化的坐標是相對於畫布中心的， 但是canvas默認的坐標系是左上角的。 我們分析下坐標系的變化，首先Y軸是相反的所以 第一個變化就是 X不變，然後Y都✖️ -1這下方向對了，差的就是偏移量。 x軸和Y軸差的偏移量都是畫布的一半寬度和高度。 這樣就實現了，到螢幕坐標的轉換了。

svg和canvas

SVG和canvas的學習我還是推薦Mdn, 大家去認真從頭擼一遍，然後再談進階，再去如何優化， 你連基本的api都不熟悉和談進階對吧。

  1. svg教程 //developer.mozilla.org/zh-CN/docs/Web/SVG/Tutorial

  2. canvas教程 //developer.mozilla.org/zh-CN/docs/Web/API/Canvas_API/Tutorial

    跟著後面學一遍，手敲一遍，自然就明白其中的奧秘。 下面👇是我用了這麼久的小經驗，和小tips

  3. svg中的path 中大寫字母和小寫字母的 區別主要是相對定位和絕對定位的關係。

  4. svg的defs標籤 不會出現在畫布上，是為了下面的組合使用的

  5. svg的g 和 symbols 都可以實現組合 ，但是symbols 有viewbox 也就是視口的概念

  6. use 復用標籤 對應上文定義的id

  7. canvas clearRect（） 清除畫布 由於canvas 每一幀都要進行重繪

  8. restore() save() 保存當前canvas 的狀態 確保不影響 其他繪圖元素

  9. isPointinPath（） 可以用來點是不是在最後一個繪製的path 中(有坑) ， 判斷點是不是在圖形內部最後用演算法去解決。

  10. beginPath() 和 closePath() 的使用

  11. 像素級別的處理 imageData 的使用

當你熟悉了這些可以進階了， 推薦學習

進階學習

深入理解canvas

//joshondesign.com/p/books/canvasdeepdive/title.html

Canvas 最佳實踐（性能優化）

//www.cnblogs.com/mopagunda/p/5622911.html

canvas 離屏渲染

//devnook.github.io/OffscreenCanvasDemo/keep-ui-responsive.html

canvas影片學習

//www.bilibili.com/video/av26151775/

推薦書籍

《HTML5 Canvas核心技術：圖形、動畫與遊戲開發》

《HTML5 2D遊戲編程核心技術》

webgl

1.學習圖形學基礎

一定一定一定要看閆令琪老師的GAMES101現代電腦圖形學。建議1.5倍速，大概一個月內可以掌握。跟著課程，把光柵渲染器和光線追蹤的作業都做掉，學了這門課，差不多圖形學基礎就打牢了。對圖形學、遊戲、3D引擎、OpenGL、Unity、UE差不多也有了基本的認識。我自己還沒有看完，還在學習中。

//www.bilibili.com/video/BV1X7411F744?from=search&seid=7915905348717479996

2.webgl 網站學習，這是我覺得品質非常不錯同時又有點深度的學習網站

//webglfundamentals.org/webgl/lessons/zh_cn/webgl-fundamentals.html

  1. 著色器和glsl
  2. 光照和顏色
  3. 如何載入外部模型
  4. 點線面如何三角化
  5. 貼圖

書籍推薦：

webgl 編程指南

3D遊戲與電腦圖形學中的數學方法

Fundamentals of Computer Graphics (4th Edition)

directx 9.0 3d遊戲開發編程基礎 這本書強力推薦 雖然是用c++寫的 ，但是他把整個渲染流程講解的很清楚，我反正看了收穫很大。這也是我們老大推薦的一本書。

框架層面

three.js

image-20210808004031389

Three.js 是最知名的 WebGL 項目，Contributions 人數高達 1313，和 React 是一個量級的，儘管它自身的定位只是渲染引擎，但社區硬是把不少遊戲引擎的功能都加上了，比如物理引擎、貼花、動畫等，在源碼中有大量例子，很適合學習，但不少重要功能，比如 gltf 載入器，都是放在 examples 目錄里，讓人感覺很不正式。

由於知名度最高，Three.js 最大的優勢就是社區強大，搜索問題能找到很多答案，也有非常多開源和商業項目使用

但 Three.js 在版本管理方面很不專業，到現在都還沒採用 semver 版本命名規範，每次發布都是一個叫 rXXX 的版本，我見過不少基於 Three.js 的項目都是固定在某個版本不敢升級了

babylonjs

image-20210808000356624

最後壓軸的是 Babylon，它也是 Sugar 最終採用的 WebGL 引擎，不僅功能強大，程式碼品質也很高，TypeScript 類型完善，幾乎每個函數都有注釋。

Babylon 在材質方面功能豐富，除了基礎的 PBR，還提供了用於皮膚的次表面渲染 SubSurface、用於車漆的 ClearCoat、用於布料的 Sheen，以及用於光碟之類的各向異性材質 Anisotropy 等等。

Babylon 最後一個亮點是正在開發 WebGPU 版本，而其他引擎都沒開始做，所以等 WebGPU 發布後，Babylon 應該是首批支援的，將得到更多關注。

AntV

image-20210808000608074

在AntV中，有好幾個不同的可視化引擎，事實上，它們是相互隔絕的，彼此獨立的。學習的時候需要單獨的去學習。ChartCube圖表魔方支援在線的生成圖表。地圖則使用L7地理空間數據可視化。

echarts

image-20210808000817240

ECharts最初是”Enterprise Charts”（企業圖表）的簡稱，來自百度EFE數據可視化團隊，是用JavaScript實現的開源可視化庫。ECharts的功能非常強大，對移動端進行了細緻的優化，適配微信小程式，支援多種渲染方式和千萬數據的前端展現，甚至實現了無障礙訪問。底層是用的z-render 這個庫去進行封裝的。還是很值的學習對的，有點類似於組件的概念，進行可配置的去展示圖表。

d3

image-20210808001245616

D3是指數據驅動文檔(Data-Driven Documents)。D3.js是一個JavaScript庫，它可以通過數據來操作文檔。D3可以通過使用HTML、SVG和CSS把數據鮮活形象地展現出來。D3嚴格遵循Web標準，因而可以讓你的程式輕鬆兼容現代主流瀏覽器並避免對特定框架的依賴。同時，它提供了強大的可視化組件，可以讓使用者以數據驅動的方式去操作DOM。被稱為可視化版的jquery。

圖形演算法

最後講一下不得不掌握的圖形演算法， 比如很簡答的例子。 判斷點是不是在任意多邊形內部對吧這就是 涉及到演算法。

我大概列舉下

  1. 判斷點是不是在任意閉合polygon中 用射線檢測法， 有內部的點，像任意方向發出一天射線計算出交點的個數， 奇數就是內部 偶數就是外部
  2. 判斷連續多邊形的方向 是順時針還是逆時針 **求面積的正負 ** 求平面的noraml (慎用) 對於凹多邊形是不準的
  3. 二維圖形下， 任意圖形的相交 推薦兩個庫 clipper 和turf 洞和外輪廓的概念，自己可以百度了解
  4. 判斷一個點 在某個向量的哪一面 上面的三點求方向逆時針還是順時針
  5. 線段求線段求相交 直線方程求焦點
  6. 求任意兩個區域的包含關係 內部 外部 相交
  7. 碰撞檢測 boundingbox 求交集

這裡我大概列了一下我工作中用到的一些演算法。

推薦一些文章：

談”求線段交點”的幾種演算法(js實現,完整版)

//www.cnblogs.com/i-gps/archive/2012/06/19/2554992.html

計算幾何與圖形學有關的幾種常用演算法

//blog.csdn.net/wilson1068/article/details/44133303

點在多邊形內演算法——判斷一個點是否在一個複雜多邊形的內部

//blog.csdn.net/hjh2005/article/details/9246967

實現多邊形的交並差還有偏移

//turfjs.org/

Clipper庫中文文檔詳解

//www.cnblogs.com/zhigu/p/11943118.html

總結

本篇文章大概就是我的個人理解哈，水平有限，能表達的就這麼多。如果有更好的歡迎補充學習和交流，文章有錯誤的歡迎指正。最後送給大家一張思維導圖，對照學習哈。我是熱愛圖形的Fly，我們下次再見👋啦。

思維導圖

資源獲得

關注公眾號【前端圖形】，回復 思維導圖 二字 可以免費獲得高清思維導圖 ，以及可視化學習影片 加文中部分書籍📚pdf版本

Tags:

VirMach 便宜 VPS

QNews

QNews