字元串匹配演算法(三)-KMP演算法
今天我們來聊一下字元串匹配演算法里最著名的演算法-KMP演算法,KMP演算法的全稱是 Knuth Morris Pratt 演算法,是根據三位作者(D.E.Knuth,J.H.Morris 和 V.R.Pratt)的名字來命名的。KMP演算法和BM的演算法思想類似,如果對BM演算法不熟悉的同學可以看這篇文章BM演算法詳解。
KMP演算法原理
KMP的演算法核心思想是,當模式串b和主串a在進行匹配的時候,如果遇到不匹配的字元,我們希望找到一種規律,可以使得模式串b多向後滑動幾位,跳過那些肯定不匹配的情況。
首先我們先明確二個定義:在模式串和主串匹配的過程中,我們把不能匹配的字元叫做壞字元,把已經匹配的那段字元叫做好前綴。在模式串和主串匹配的過程中,當遇到壞字元後,對於已經比對過的好前綴,能否找到一種規律,將模式串可以滑動多位呢。
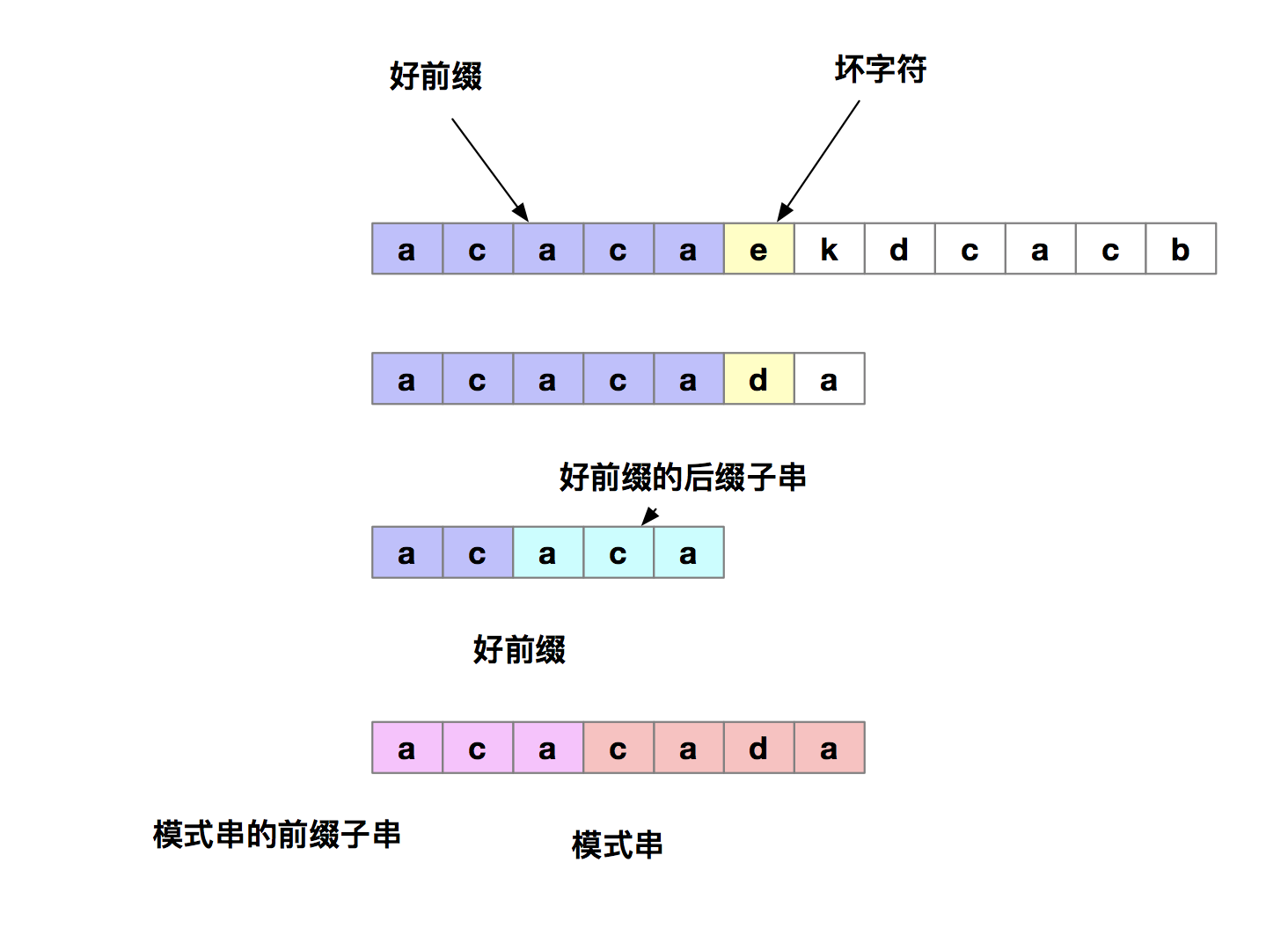
其實我們只需要拿好前綴本身,在他的後綴子串中,查找最長的那個可以跟好前綴的前綴子串匹配的。假設最長可匹配的那部分前綴子串是{u},長度是k。我們可以把模式串一次性先後滑動j-k位,即當匹配到壞字元時,我們把j更新為k,然後i不變,然後再繼續匹配。
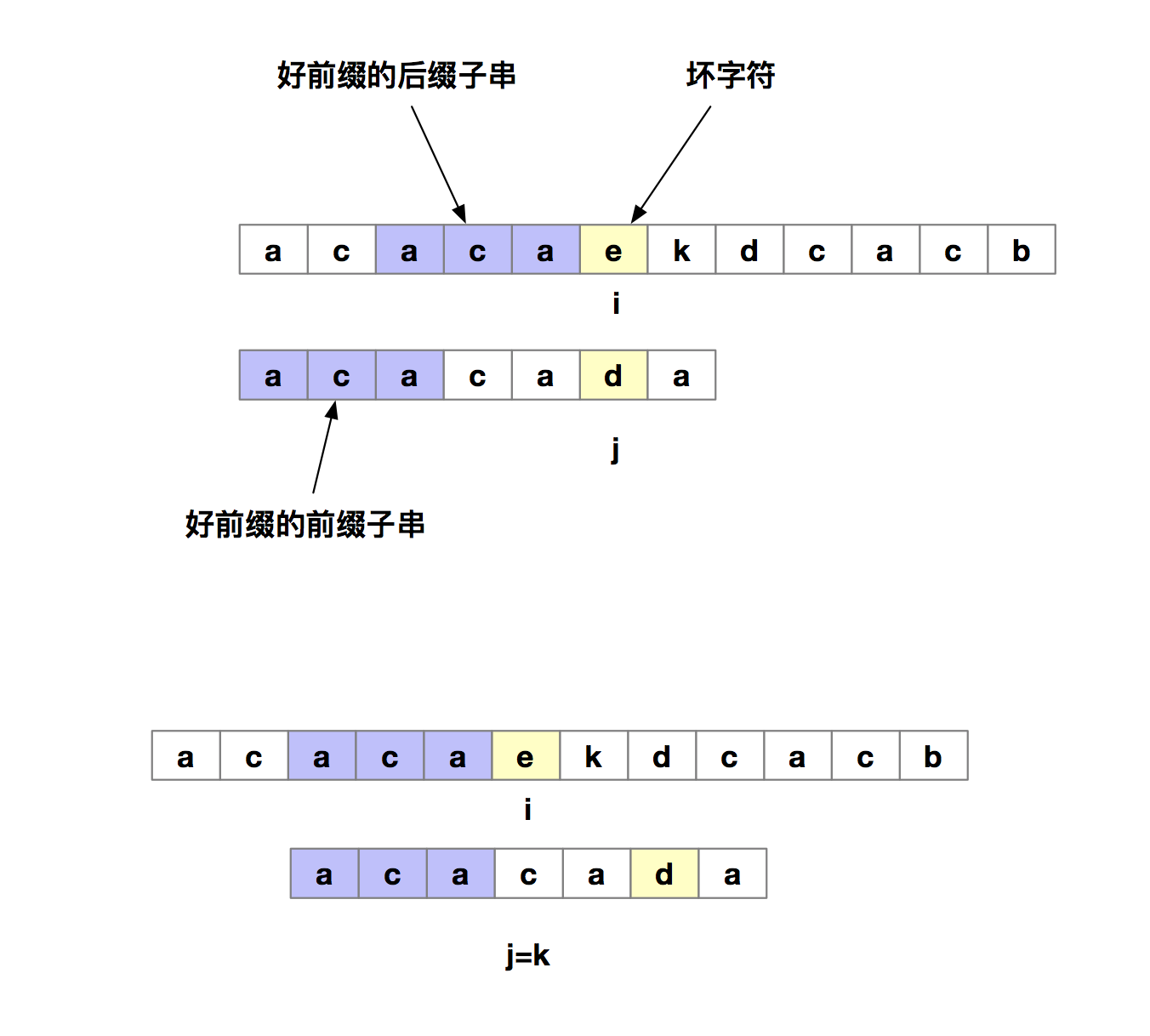
下面我們再明確兩個定義,我們把好前綴的所有後綴子串中,最長的可以匹配前綴子串的那個後綴稱為最長可匹配後綴子串,對應的前綴子串叫做最長可匹配前綴子串。那如何來求好前綴的最長可匹配前綴和後綴子串呢?
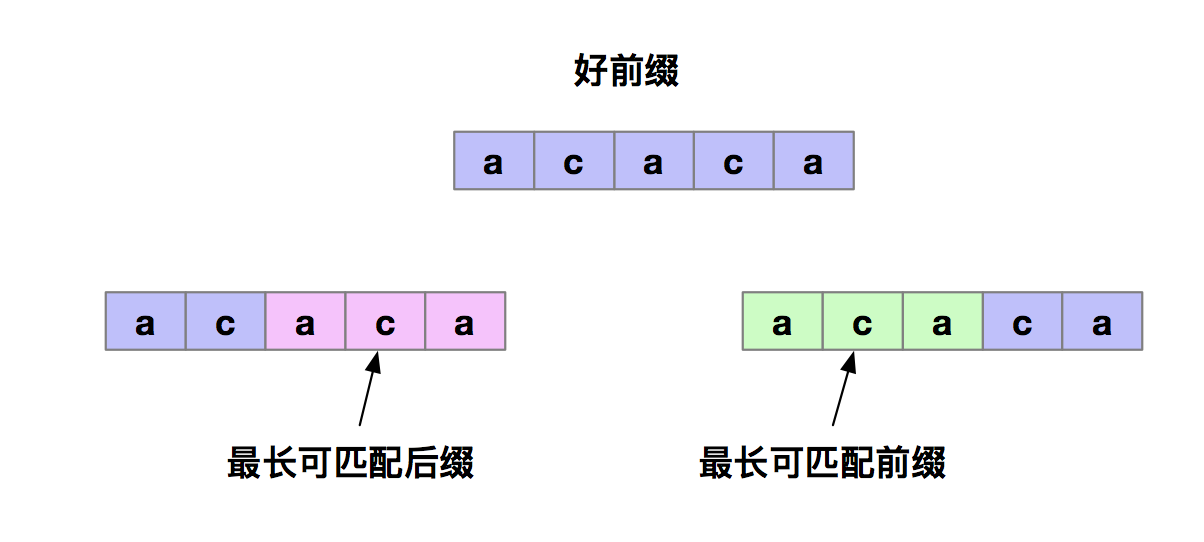
KMP演算法是通過構建了一個數組來求的。該數組的下標是每個前綴結尾字元下標,該數組的值是這個前綴的最長可以匹配前綴子串的結尾字元下標。我們把這個數組定義為 next 數組,同時也可以稱為是失效函數。如下圖所示。

next數組的計算方法
我們來思考這麼一個問題。如果next[i-1]=k-1,也就是說子串b[0, k-1]是b[0, i-1]的最長可匹配前綴子串。如果子串 b[0, k-1]的下一個字元 b[k],與 b[0, i-1]的下一個字元 b[i]匹配,那麼子串 b[0, k]就是 b[0, i]的最長可匹配前綴子串。所以,next[i]等於 k。如果 b[0, k-1]的下一字元 b[k]跟 b[0, i-1]的下一個字元 b[i]不相等呢?那我們這個時候就不能簡單地通過 next[i-1]得到 next[i]了。這個時候該怎麼辦呢?我們假設 b[0, i]的最長可匹配後綴子串是 b[r, i]。如果我們把最後一個字元去掉,那 b[r, i-1]肯定是 b[0, i-1]的可匹配後綴子串,但不一定是最長可匹配後綴子串。所以,既然 b[0, i-1]最長可匹配後綴子串對應的模式串的前綴子串的下一個字元並不等於 b[i],那麼我們就可以考察 b[0, i-1]的次長可匹配後綴子串 b[x, i-1]對應的可匹配前綴子串 b[0, i-1-x]的下一個字元 b[i-x]是否等於 b[i]。如果等於,那 b[x, i]就是 b[0, i]的最長可匹配後綴子串。可是,如何求得 b[0, i-1]的次長可匹配後綴子串呢?次長可匹配後綴子串肯定被包含在最長可匹配後綴子串中,而最長可匹配後綴子串又對應最長可匹配前綴子串 b[0, y]。於是,查找 b[0, i-1]的次長可匹配後綴子串,這個問題就變成,查找 b[0, y]的最長匹配後綴子串的問題了。按照這個思路,我們可以考察完所有的 b[0, i-1]的可匹配後綴子串 b[y, i-1],直到找到一個可匹配的後綴子串,它對應的前綴子串的下一個字元等於 b[i],那這個 b[y, i]就是 b[0, i]的最長可匹配後綴子串。這塊比較繞,可以先看程式碼,然後反過來多讀幾遍。
#b表示模式串
#m表示模式串的長度
def getNext(b,m):
next=[-1]*m
k=-1
for i in range(1,m):
while k!=-1 and b[k+1]!=b[i]:
k=next[k]
if b[k+1]==b[i]:
k=k+1
next[i]=k
return next
我們有了next數組後,就可以動手來實現kmp演算法了。
#b表示模式串
#m表示模式串的長度
def getNext(b,m):
next=[-1]*m
k=-1
for i in range(1,m):
while k!=-1 and b[k+1]!=b[i]:
k=next[k]
if b[k+1]==b[i]:
k=k+1
next[i]=k
return next
def kmp(a,n,b,m):
next=getNext(b,m)
print(next)
j=0
for i in range(n):
while j>0 and a[i]!=b[j]:
j=next[j-1]+1
if(a[i]==b[j]):
j=j+1
#找到匹配模式串的了
if(j==m):
return i-m+1
return -1
到此為止,我們的kmp演算法就學完了。更多硬核知識,請關注公眾號。


