為了讓她學畫畫——熬夜用canvas實現了一個畫板
前言
大家好,我是Fly, canvas真是個強大的東西,每天沉迷這個無法自拔, 可以做遊戲,可以對圖片處理,後面會給大家分享一篇,canvas實現兩張圖片找不同的功能, 聽著是不是挺有意思的, 有點像遊戲 找你妹,但是這都不是本篇文章想要表達的重點,讀完今天這篇文章,你可以學到什麼呢
- Canvas 實現一個簡單的畫版小工具
- Canvas 畫出平滑的曲線, 這是本篇文章的重點
這時候有人問我她??, 我的心裡沒有她的,只有你們coder, 下面一起學習吧,預計閱讀10分鐘。
canvas實現一個畫版小工具
因為也比較簡單,我大概說下思路:
- 首先我對canvas 畫布堅監聽3個事件, 分別是mouseMove,mouseDown,mouseUp 三個事件, 同時創建了isDown 這個變數, 用來標記當前畫圖是不是開啟
- 當我們按下滑鼠 也就是mouseDown 事件, 表示開始畫筆,有一個初始的點, 並把isDown 設置為true, 然後緊著呢開始移動, 可以確定直線的端點, 然後再把直線的端點設置為下一條直線的起始點, 不斷地重複這個過程, mousueUp 將isDown 這個變數設置為false, 同時清空開始點和結束點
- 通過mouseMove事件不斷採集滑鼠經過的坐標點,當且僅當isDown 為true(即處於書寫狀態)時將當前的點通過canvas的LineTo方法與前面的點進行連接、繪製;
程式碼如下:
class board {
constructor() {
this.canvas = document.getElementById('canvas')
this.canvas.addEventListener('mousemove', this.move.bind(this))
this.canvas.addEventListener('mousedown', this.down.bind(this))
this.canvas.addEventListener('mouseup', this.up.bind(this))
this.ctx = this.canvas.getContext('2d')
this.startP = null
this.endP = null
this.isDown = false
this.setLineStyle()
}
setLineStyle() {
this.ctx.strokeStyle = 'red'
this.ctx.lineWidth = 1
this.ctx.lineJoin = 'round'
this.ctx.lineCap = 'round'
}
move(e) {
if (!this.isDown) {
return
}
this.endP = this.getPot(e)
this.drawLine()
this.startP = this.endP
}
down(e) {
this.isDown = true
this.startP = this.getPot(e)
}
getPot(e) {
return new Point2d(e.offsetX, e.offsetY)
}
drawLine() {
if (!this.startP || !this.endP) {
return
}
this.ctx.beginPath()
this.ctx.moveTo(this.startP.x, this.startP.y)
this.ctx.lineTo(this.endP.x, this.endP.y)
this.ctx.stroke()
this.ctx.closePath()
}
up(e) {
this.startP = null
this.endP = null
this.isDown = false
}
}
new board()
point2d是我自己寫的一個2d點的一個類,不清楚的同學可以看我前幾篇文章, 這裡就不重複闡述了。我們看下gif:

細心的同學可能發現,畫的線折線感比較強,出現這個本質的原因—— 就是我們畫出的線其實是一個多段線polyline, 連接兩個點之間的線是直線
如何畫出平滑的曲線
想起曲線,就不得不提到貝塞爾曲線了,我之前的文章有系統的介紹過貝塞爾曲線,以及貝塞爾曲線方程的推導過程—— 傳送門
canvas 肯定是支援貝塞爾曲線的quadraticCurveTo(cp1x, cp1y, x, y) , 主要是一個起始點, 一個終點,一個控制點。 其實這裡可以用一個巧妙的演算法去解決這樣的問題。
獲取二階貝塞爾曲線資訊的演算法
假設我們在滑鼠移動的過程中有A、B、C、D、E、F、G、這6個點。如何畫出平滑的曲線呢, 我們取B點和C點的中點B1 作為第一條貝塞爾曲線的終點,B點作為控制點。如圖:
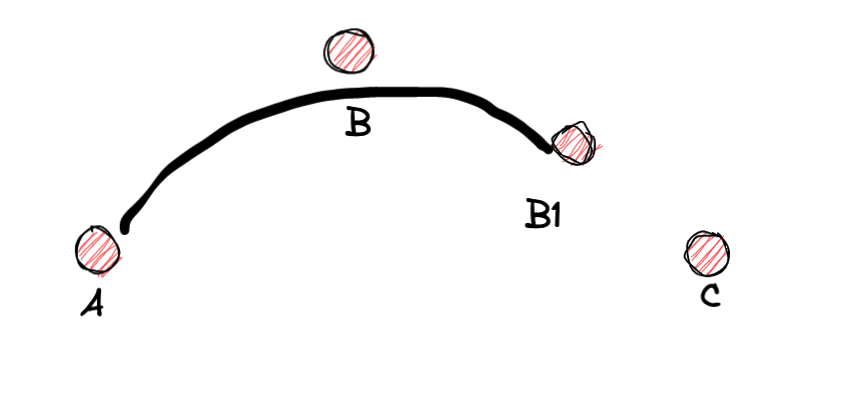
接下來呢 算出 cd 的中點 c1 以 B1 為起點, c點為控制點, c1為終點畫出下面圖形:
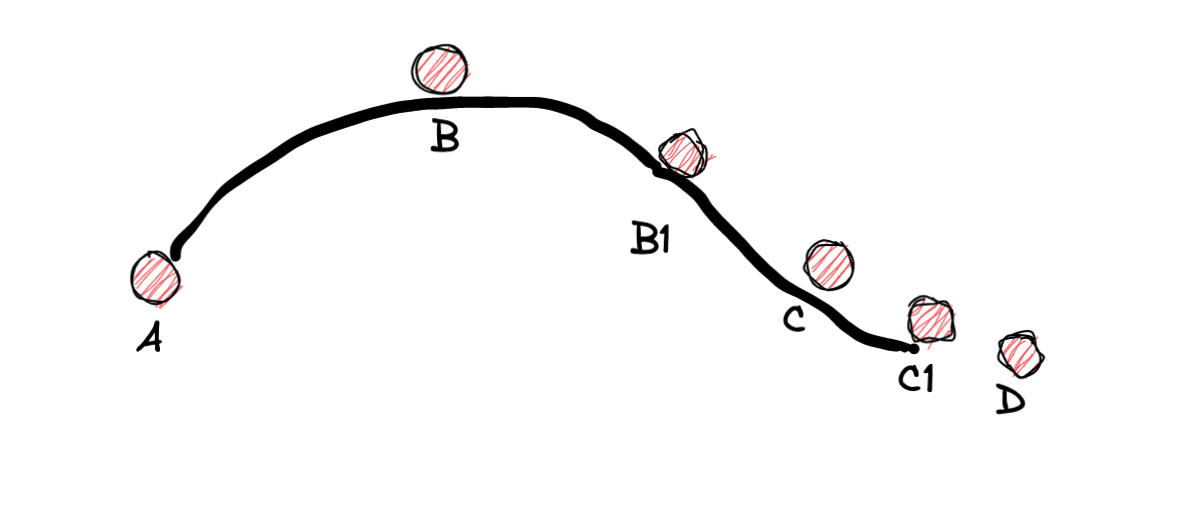
然後後面按照這樣的步驟不斷畫下去,就可以獲得平滑的曲線了。 理論基礎我們明白了, 我們改造上面的畫線的方法:
實現畫出平滑的曲線
上面涉及到求兩個點的中間坐標:其實兩個坐標的x 和y 分別除以2: 程式碼如下:
getMid(p1, p2) {
const x = (p1.x + p2.x) / 2
const y = (p1.y + p2.y) / 2
return new Point2d(x, y)
}
我們畫出二階貝塞爾曲線至少所示需要3個點, 所以我們需要數組去存放移動過程中所有的點的資訊。
我先實現畫貝塞爾曲線的方法:
drawCurve(controlP, endP) {
this.ctx.beginPath()
this.ctx.moveTo(this.startP.x, this.startP.y)
this.ctx.quadraticCurveTo(controlP.x, controlP.y, endP.x, endP.y)
this.ctx.stroke()
this.ctx.closePath()
}
然後在修改move 中的事件
move(e) {
if (!this.isDown) {
return
}
this.endP = this.getPot(e)
this.points.push(this.endP)
if (this.points.length >= 3) {
const [controlP, endP] = this.points.slice(-2)
const middle = this.getMid(controlP, endP)
this.drawCurve(controlP, middle)
this.startP = middle
}
}
這裡實現永遠取倒數後兩個點,然後畫完貝塞爾曲線後再將 這個貝塞爾的終點設置為開始點方便下次畫。這樣是能保證畫出連續的貝塞爾曲線的。
我們看下gif 圖:
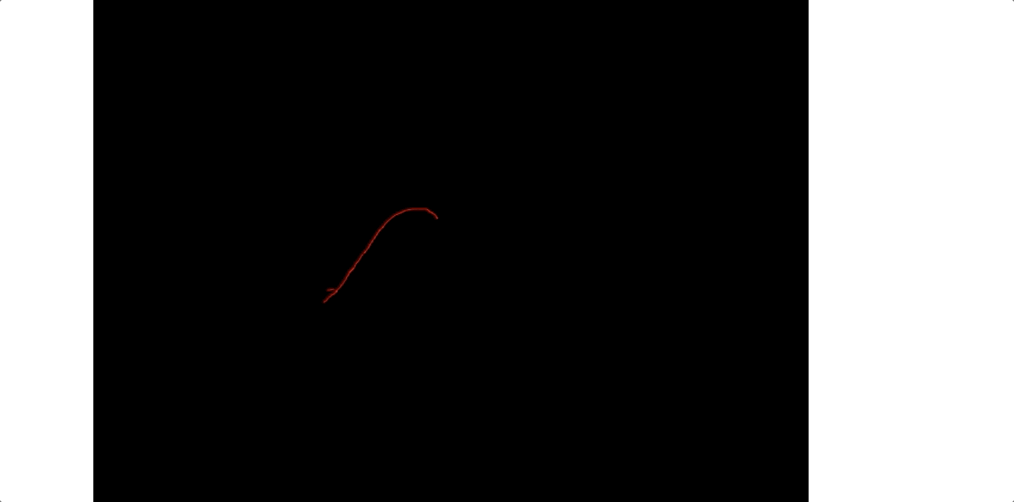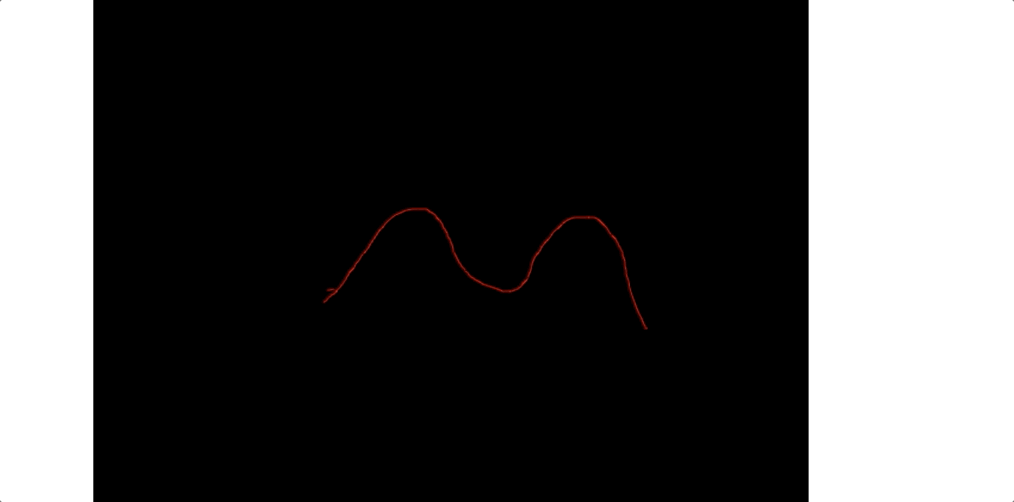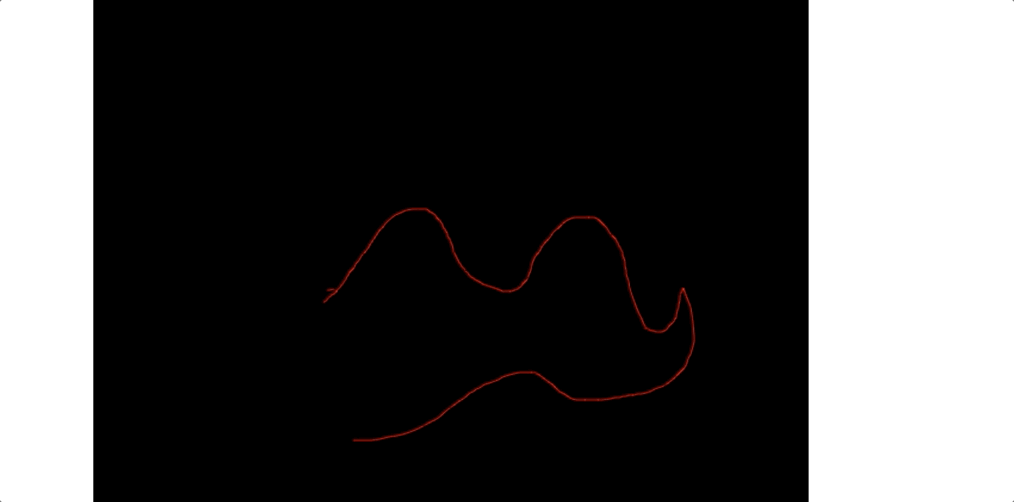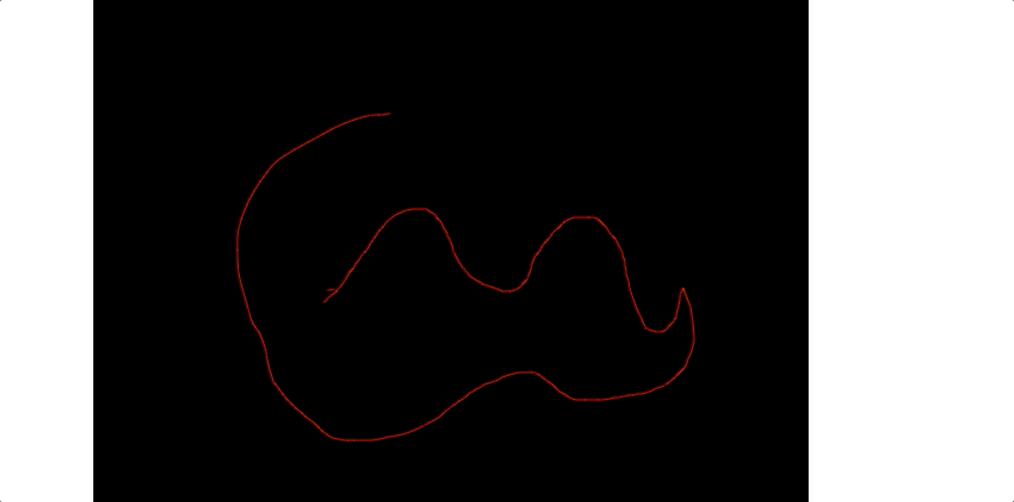
總結
至此本篇文章也算是寫完了, 如果你有更好的思路歡迎和我交流,我這只是粗略的表示。canvas畫連續平滑的曲線重點——還是怎麼去找控制點這一點非常的重要哈!下一篇文章預告: canvas的離屏渲染和webworker的使用。
學習交流
本篇文章所有程式碼都在我的github上歡迎fork和stark。對可視化感興趣的可以關注我的公眾號【前端圖形】,加群 一起學習交流吧!


