canvas實現任意正多邊形的移動(點、線、面)
我在上一篇文章簡單實現了在canvas中移動矩形(點線面),不清楚的小夥伴請看我這篇文章:
-
判斷點與點之間的距離
-
判斷點與直線的關係(叉乘的使用)
-
canvas中如何畫出正n邊形。(旋轉)
其實我上面說了這麼多,其實就是為了在2d圖形做一個效果就是 snap ——吸附,判斷當前點與當前畫布上多邊形的關係。
吸附——實現點
讀者你可以思考下,如果要你去做你會怎麼去做呢? 假設畫布上有很多多邊形,還有很多點。有人說了,哪一個靠近它不就是哪一個。ok 你答對了,其實就是去判斷當前點和畫布上所有的點去比對,哪一個離的近,就是選中的哪一個點,這裡會涉及到一個查詢性能問題? 有同學就會問如果畫布中有很多點呢?我們難道就要一個個去遍歷比較大小嘛,當然不是這裡給大家科普一下一個空間幾何索引演算法Rbush
RBush是一個高性能JavaScript庫,用於點和矩形的二維空間索引。它基於優化的R樹數據結構,支援批量插入。
我後面有時間會帶大家擼一遍Rbush的,這裡我給出
const current = 0;
const map = new Map();
constructor(x,y) {
this.x = x || 0;
this.y = y || 0;
this.id = ++current;
map.set(this.id,[x,y]);
}
// 增加到Map上
add2Map() {
pointMap.push(this)
return this
}
//用來隨機生成一個點
random(width,height){
this.x = Math.random() * width;
this.y = Math.random() * height;
return this;
}
// 取絕對值
abs() {
return [Math.abs(this.x), Math.abs(this.y)]
}
//計算兩個點之間的距離
distance(p) {
const [x,y] = this.clone().sub(p).abs();
return Math.sqrt(x*x + y * y);
}
我又重新寫了一個畫多邊形的方法程式碼如下:
// 畫多邊形
function drawAnyPolygon(points) {
if(!Array.isArray(points)) {
return;
}
ctx.strokeStyle = 'black'
ctx.setLineDash([]);
ctx.beginPath();
const start = points[0];
ctx.moveTo(start.x,start.y)
points.slice(1).forEach(item => {
ctx.lineTo(item.x,item.y)
})
ctx.closePath()
ctx.stroke()
}
這個沒什麼最重要的是什麼呢,我們如何根據一個點去生成正多邊形的點集合
CANVAS中如何畫正多邊形?
這裡我們看下多邊形的定義:
正多邊形是指二維平面內各邊相等,各角也相等的多邊形,也叫正多角形。
去比較滑鼠的點和畫布中的點的距離了。我們先看第一部分根據類型生成點:
// 根據移動的類型重新生成點
function generatePointsByType(mousePoint,type = 'point',width = 200, height = 200) {
const results = [];
const { x, y } = mousePoint;
const moveVec = end.clone().sub(start);
const p1 = new Point2d(x- width /2, y - height/2).add2Map();
const p2 = new Point2d(x+ width / 2, y - height/2).add2Map();
const p3 = new Point2d(x+ width / 2, y + height/2).add2Map();
const p4 = new Point2d(x - width / 2, y + height/2).add2Map();
return [p1,p2,p3,p4]
}
這裡有一點要注意的是就是p1,p2,p3,p4 滿足的是順時針,因為我們canvas畫圖是從左上—–>左下的。 這一點大家在自己調試的要十分注意!!add2Map, 就是把點加入到Map中。我在上面補充上。我給出下一部分程式碼:比較滑鼠的點和畫布中的點之間的大小。
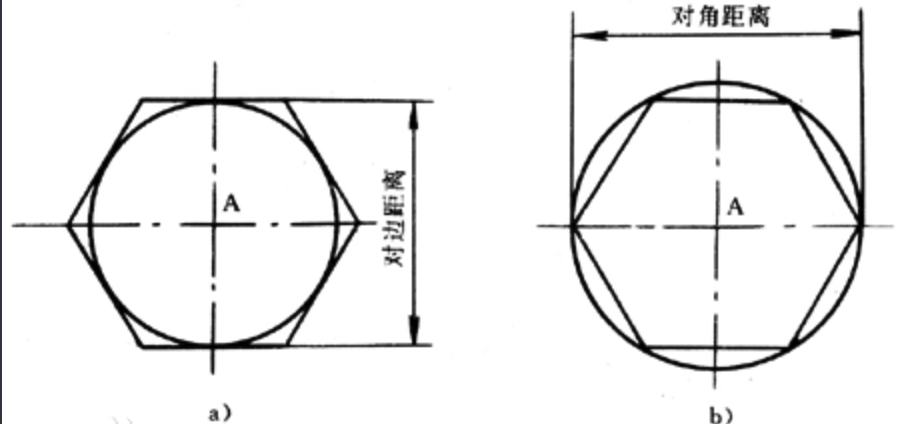
從圖中我們可以得到: 正多形的形成 無非就是兩種
-
以當前點為圓心、畫出一個外接圓、然後呢 根據邊數進行等分
-
以當前點為圓心、畫出一個內接圓、然後呢 根據邊數進行等分
原理我們知道了,應用到我們canvas怎麼去實現呢? 其實也很簡單,我們以圓心和圓上的一點,作為起始的向量。然後不斷地旋轉 2π/n 的角度 就可以得到所有的點了。 有了點我們就可以畫出正多邊形了。 這裡是外接圓算多邊形的思路,至於內接圓怎麼去算, 給大家一個課後思考題🤔自己去想一下。 我給出以下程式碼實現:
第一部分點的繞著某一個中心點旋轉的:
rotate(center, angle) {
const c = Math.cos( angle ), s = Math.sin( angle );
const x = this.x - center.x;
const y = this.y - center.y;
this.x = x * c - y * s + center.x;
this.y = x * s + y * c + center.y;
return this;
}
這裡的大概思路向量的旋轉然後在加上中心點的位置。 如果看不懂的話, 我給大家找一個推導過程:
第二部分就是如果生成多邊形的頂點了:
function getAnyPolygonPoints(start, end, n = 3) {
const angle = (Math.PI * 2) / n
const points = [end]
for (let i = 1; i < n; i++) {
points.push(
end
.clone()
.rotate(start.clone(), angle * i)
.add2Map()
)
}
return points
}
接下我就給大家看下 n = 5|10 |20 |50 的 這些正多邊形。然後你會發現隨著邊數的增加,我們畫的多邊形越越像個圓了。
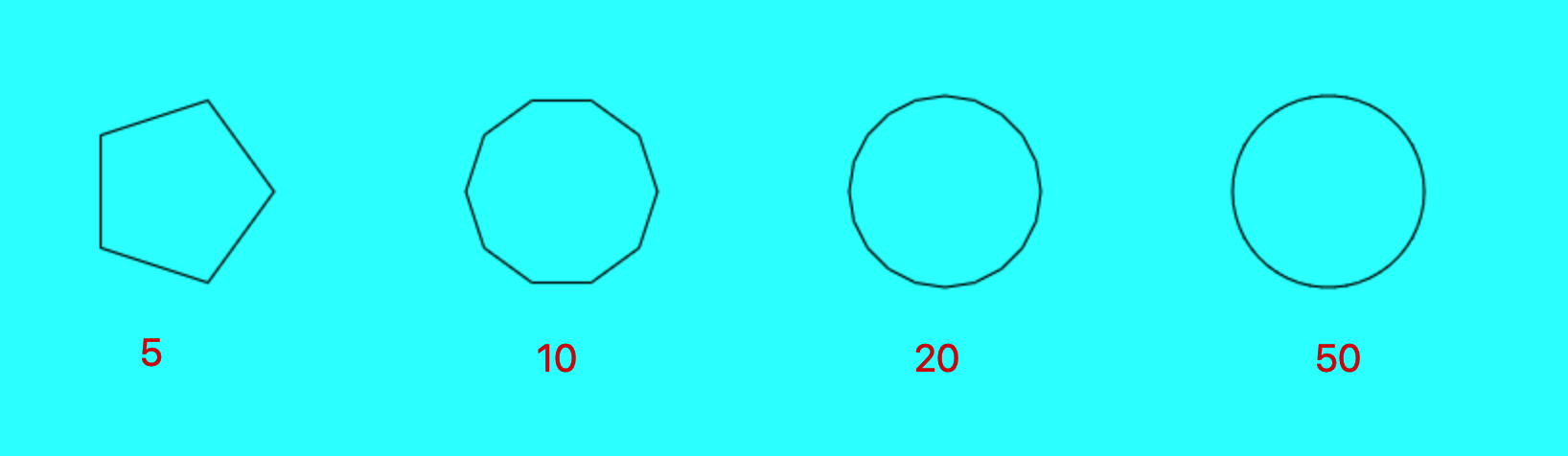
有沒有解鎖你們的新世界?各位讀者們。看到這裡如果覺得對你有幫助的話。點個贊繼續往下看吧。 👇還有一些數學方法的介紹。
實現任意正多邊形點的移動
我們設想滑鼠不停地在畫布上移動,我肯定哪一個點離我近,我就去選擇哪一個點。 所以也就是不停的比較滑鼠移動的點和已經存在的點的距離做判斷。ok思路有了,我給出以下程式碼:
function calcClosestPoint() {
const minMap = []
for (let value of pointMap) {
const dis = value.distance(start.clone())
minMap.push({
這段程式碼肯可能要講的就是兩點之間求距離? 這個就很簡單了,就是兩個坐標相減求絕對值,然後開方。一般人肯定會這麼想對吧,一開始我也是這麼想的。 這麼想沒問題, 但是其實我不不需要開方,我們要比較的是距離。這裡會有一個性能小優化。因為你要開方,然後cpu又去計算,如果畫布中點的數量過多呢,並且數字很大的情況下。程式碼如下:
distance(p) {
const [x, y] = this.clone().sub(p).abs()
return x * x + y * y
}
distanceSq(p) {
const [x, y] = this.clone().sub(p).abs()
return Math.sqrt(x * x + y * y)
}
找到最小的點,我們就可以重複上一篇文章實現移動了。這裡就不做過多講解了,不清楚的小夥伴,可以去看過上一篇文章。 給出以下程式碼:
//畫出任意多邊形 滿足順時針方向
function drawAnyPolygon(points) {
if (!Array.isArray(points)) {
return
}
ctx.strokeStyle = 'black'
ctx.setLineDash([])
ctx.beginPath()
// 存在移動的點
if (movePoint.length > 0) {
const moveVec = end.clone().sub(start)
points = points.map((item) => {
if (item.equal(movePoint[0])) {
return item.clone().add(moveVec)
}
return item
})
}
ctx.moveTo(points[0].x, points[0].y)
points.slice(1).forEach((item) => {
ctx.lineTo(item.x, item.y)
})
ctx.closePath()
ctx.stroke()
}
canvas.addEventListener('click', (e) => {
if (e.altKey) {
isMove = false
return
}
isMove = !isMove
const x = e.clientX
const y = e.clientY
start = new Point2d(x, y)
movePoint.length = 0
movePoint.push(calcClosestPoint())
isSelect = true
})
這裡我點擊滑鼠的以下就確定移動的點 和移動向量的起點,movePoint 其實是所有要移動的點。直接看效果圖吧。

實現任意正多邊形線的移動
點的移動我們實現了,我們滑鼠的點的那一刻,我們該如何確定點擊的是線呢,這也歸咎到一個數學問題? 就是比較點到直線的距離, 點到直線的距離,第一種解法就是直線方程去求解。 直線的直線方程是什麼?
求點到直線的距離方法1
設直線 L 的
同理可知,當P(x0,y0),直線L的解析式為y=kx+b時,則點P到直線L的距離為
考慮點(x0,y0,z0)與空間直線x-x1/l=y-y1/m=z-z1/n,有d=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)
也就是兩個點算出斜率和截距,但是要考慮直線與Y軸的特殊情況,也就是斜率無窮大的時刻。 這時候的距離就是x坐標相減。這樣我們可以計算點到直線的距離,然後比較找出距離最小的線,接著找出移動的點就可以了。但這不是最優解,
求點到直線的距離方法2
首先我問一個問題哈? 向量的叉乘的幾何意義是什麼, 就是兩個向量圍成的平行四邊形的面積。 我們計算點到直線的距離不就是計算,平行四邊形的高嘛, 所以只要算出面積再除以底邊就可以算出點到直線的距離了。 哈哈哈哈,是不是再一次被數學的魅力征服了。我給大家看個圖吧:
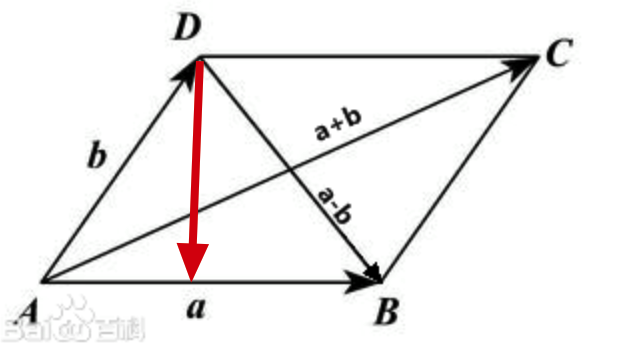
紅色的線就是點到直線的距離。 我們直接開始coding了,理論有了直接開干。
首先寫一個點轉為線段的一個方法,因為我們是首尾相連,所以點的個數,最後一個應該是和開始點相同的。
function points2Segs(points) {
const start = points[0]
points.push(start)
const segs = []
points.forEach((point, index) => {
if (index !== points.length - 1) {
segs.push([point, points[index + 1]])
}
})
return segs
}
叉乘的方法如下:
cross(v) {
return this.x * v.y - this.y * v.x
}
計算點到直線的距離如下:
function pointDistanceToLine(target, line) {
const [start, end] = line
const vec1 = start.clone().sub(target)
const vec2 = end.clone().sub(target)
return vec1.clone().cross(vec2) / start.clone().distanceSq(target)
}
// 找出最近的線
function calcClosestLine() {
let minMap = []
segs.forEach((line) => {
const dis = pointDistanceToLine(start, line)
minMap.push({
dis,
line,
})
})
minMap = minMap.sort((a, b) => a.dis - b.dis)
// 找出最近的直線然後將點放入到movePoint 中其實就好了
movePoint.push(
移動那邊程式碼改寫一下:
if (movePoint.length > 0) {
const moveVec = end.clone().sub(start)
points = points.map((item) => {
// 線的移動對應的是兩個點 面的話應該就是所有的點
if (item.equal(movePoint[0]) || item.equal(movePoint[1])) {
return item.clone().add(moveVec)
}
return item
})
}
直接來看效果:

完美實現很感謝你還能看到這裡。 到這裡因為點和線其實都會了,面就是所有的點移動這個是沒什麼難度的,後面大家可以自己去練習一下。
總結
本篇文章主要是介紹了2d 下圖形的移動, 點線面。 本質上都是點的移動,加上一個移動向量。核心就是這個,其實還有很多東西是需要大家慢慢體會的。一個閉合區域的形成,點的順序,肯定是首尾相連的,按照某一個方向。還有就是對於叉乘、點乘的一些理解。 結合到實現項目中可以靈活運用。本篇文章的所有程式碼都在我的