【翻譯】擬合與高斯分布 [Curve fitting and the Gaussian distribution]

  • 2021 年 7 月 21 日
  • 筆記

參考與前言

  1. 英文原版 Original English Version：//fabiandablander.com/r/Curve-Fitting-Gaussian.html
  2. 原文中有超多參考，原文參考就不一一複製過來了哈

注意：此文主要是 英文原版的自製中文翻譯 (已徵得原作者同意)，而且可能進行了一定的壓縮/添加操作，請學有餘力者跳轉至原版鏈接

Note: This post was originally published on  //fabiandablander.com/

沒錯，這裡是我看大佬的傑作，一開始提出的問題，其實類似於回顧吧 回顧為什麼之旅：為什麼在擬合中是高斯分布？高斯過程又在幹什麼？而這篇主要是針對前者的回復，擬合和高斯分布 (後者關於高斯過程中的下次再搜一搜) 然後這篇英文文章真的超贊！作者還有其他系列的也超贊！主要是看的過程還可以學歷史🥰hhhh 由淺入深，看看我有沒有精力再把第二篇關於高斯的翻完。

省流版：中心極限定理

擬合的過程

一條線在平面坐標系的表示主要是斜率(\(b_1\))和截距(\(b_0\))（也就是x=0時，y的那個點）

\[y=b_0+b_1x
\]

那麼假設我們擁有很多個點後去得到 \(b_1\) 和 \(b_0\) 。先從簡單的來吧

  1. 假設只有一個點的時候，我們的擬合結果可能像第一幅，也就是無數條線，無法確定 \(b_1\) 和 \(b_0\)​
  2. 當我們有兩個點時 我們可以唯一確定下來這條直線是誰
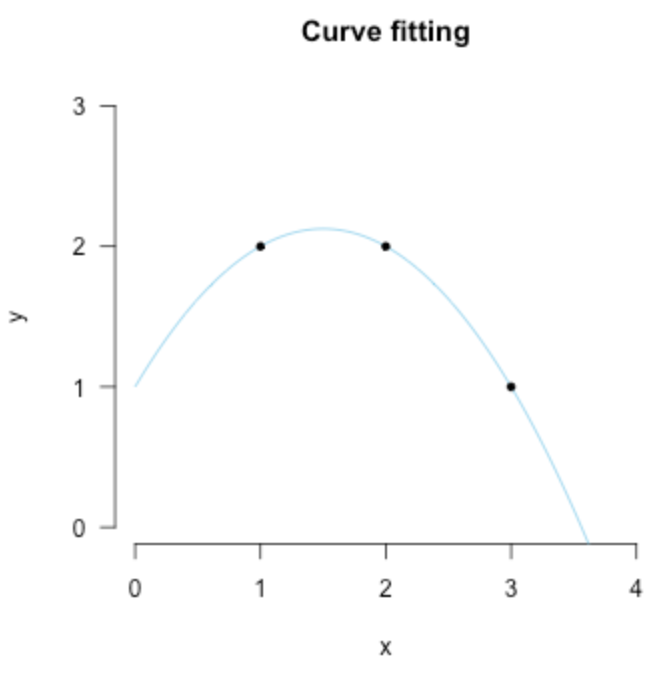
  3. 當我們有三個點時，我們無法找到一條直線把三個點都穿過，但是可以想想，是否畫出來的線中 有較好的線(擬合誤差較小)



那麼接下來，讓我們繼續思考，第三幅圖我們應該怎樣去擬合？或許是再加一個參數 \(b_2\)​ ？那 \(b_2\)​ 乘什麼呢？還是簡單起見，我們就直接按 \(x\)​ 的指數上去把給他乘一個 \(x^2\)​ ，那現在線方程變成了這樣：

\[y=b_0+b_1x+b_2x^2
\]

現在是否發現了一些事情，在絕對的情況下，兩個參數 \((b_0,b_1)\)​ 用兩個點 \(P_1,P_2\)​ ，三個參數\((b_0, b_1, b_2)\)​ 用三個點 \(P_1,P_2, P_3\)​​

另外，如果我們同時可以這麼去看點 \(P’=(y,x_1,x_1^2)\)​ ，還是第三幅圖的點坐標，我們可以用線性代數里的矩陣形式去表示等式：

\[\begin{aligned}
\mathbf{y} &=\mathbf{X} \mathbf{b} \\
\left(\begin{array}{l}
2 \\
1 \\
2
\end{array}\right) &=\left(\begin{array}{ccc}
1 & 1 & 1 \\
1 & 3 & 9 \\
1 & 2 & 4
\end{array}\right) \cdot\left(\begin{array}{l}
b_{0} \\
b_{1} \\
b_{2}
\end{array}\right)
\end{aligned}
\]

而這也就是上面的擬合結果，然後我們再思考一下：這樣的結果有什麼缺點？

  1. 過擬合：對現在已知的數據點擬合完美，但是對未來的數據點可能就不OK了

  2. 這個數據的意義是什麼：we haven』t really explained anything

    引用Fisher的話:

    The objective of statistical methods is the reduction of data. A quantity of data, which usually by its mere bulk is incapable of entering the mind, is to be replaced by relatively few quantities which shall adequately represent […] the relevant information contained in the original data. (Fisher, 1922, p. 311)

總結起來就是：沒錯 我們擬合了這條線，但是我們並沒有降低數據量，三個點還是需要對應的三個參數，那是否n個點就需要對應的n個參數呢？所以引出了回答上面的高亮部分：哪條直線更好？

“最好”的擬合

將超定(overdetermined)減小到確定(determined)情況並不可以。但是可以將超定轉到欠定。為了達到這一目的呢，我們需要做出合理的假設說明觀測點（數據點）是有對應的誤差的，例如這樣子：

\[\begin{aligned}
&1=b_{0}+4 b_{1}+\epsilon_{1} \\
&4=b_{0}+2 b_{1}+\epsilon_{2} \\
&3=b_{0}+1 b_{1}+\epsilon_{3}
\end{aligned}
\]

而這裡的 \((\epsilon_{1}, \epsilon_{2}, \epsilon_{3})\)​​​​ 是unobserved quantities 未知誤差值。而這一步沒錯又引入了未知量，所以我們再次以少的數據（少的方程）去解多的參數量，所以我們的之前的超定就變成了欠定系統求解了

正如前面所說，只有一個點時，如果沒有其他限制，我們就有無數條直線說 我們擬合成功了。一樣的道理在這裡，我們需要添加限制，例如前面例子我需要經過這個點的線同時儘可能平行x軸，這就是一個限制。而對於現在這個問題 法國數學家Adrien-Marie Legendre 提出了著名的 最小二乘法

在上面那個例子中，通過最小二乘的誤差限制，只會出現一條線滿足最小的誤差。因此，對於所有的其他欠定系統我們都可以這樣：添加最小二乘誤差的限制，例如下圖：



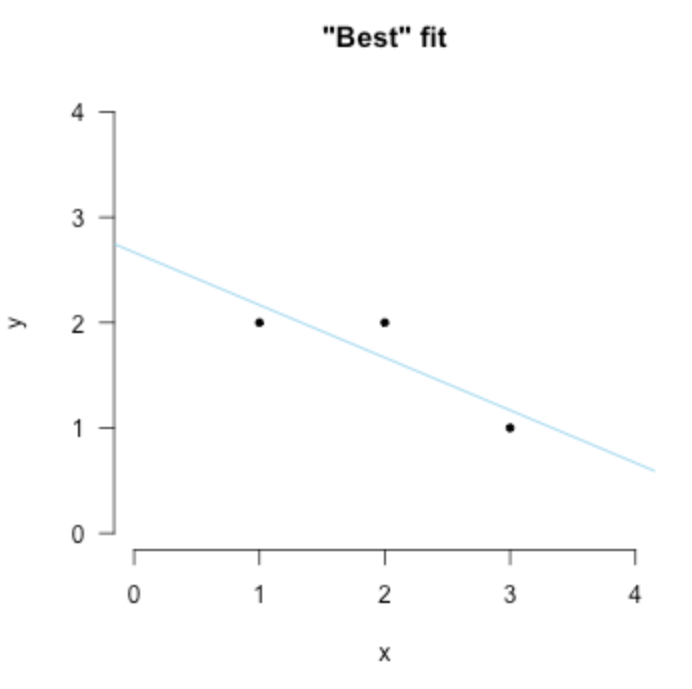
同時最小二乘法的發展也是數理統計的分水嶺——Stephen Stigler 將其重要性比作數學中微積分的發展。那麼理論上我們已經知道可以這樣去找到最好的擬合。那數學上我們怎麼知道是具體哪一條，這裡提到了兩種，一種是由Legendre提出的優化；另外一種是幾何意義上的直觀insight

Least squares I: Optimization

首先我們的目標是找到最小的均方誤差。從簡單入手呢，就是直接求數據的平均值，然後再去減他們，類似於這樣：

\[\begin{aligned}
y’&=y-\frac{1}{n}\sum_{i=1}^n y_i \\

x’&=x-\frac{1}{n}\sum_{i=1}^n x_i
\end{aligned}
\]

因為這樣的最小化誤差和 \(b_0\)​​ 無關，所以我們就可以不去預估 \(b_0\)​ 是多少了

  1. 首先我們觀測到數據點 \(y_i\) 我們直線給出的預估是 \(x_ib_1\) ，所以誤差就是： \(\epsilon_{i}=y_{i}-x_{i} b_{1}\)​，我們把有的所有數據都加起來 那總誤差就是這樣的：

    \[\sum_{i=1}^{n} \epsilon_{i}^{2}=\sum_{i=1}^{n}\left(y_{i}-x_{i} b_{1}\right)^{2}
    \]

  2. 現在我們就去找哪一個 \(b_1\) 可以得到最小的總誤差，這裡用 \(\hat b_1\) 表示

    \[\hat{b}_{1}=\underbrace{\operatorname{argmin}}_{b_{1}}\left(\sum_{i=1}^{n}\left(y_{i}-x_{i} b_{1}\right)^{2}\right)
    \]

  3. 就像我們找曲線的最低點一樣，求導，導數等於0，值小於其周圍值的地方就是我們想要的點。那麼在這個問題中，我們就是這樣子做：

    \[\begin{aligned}
    0 &=\frac{\partial}{\partial b_{1}}\left(\sum_{i=1}^{n}\left(y_{i}-x_{i} b_{1}\right)^{2}\right) \\
    0 &=\frac{\partial}{\partial b_{1}}\left(\sum_{i=1}^{n} y_{i}^{2}-2 \sum_{i=1}^{n} y_{i} x_{i} b_{1}+\sum_{i=1}^{n} x_{i}^{2} b_{1}^{2}\right) \\
    0 &=0-2 \sum_{i=1}^{n} y_{i} x_{i}+2 \sum_{i=1}^{n} x_{i}^{2} b_{1} \\
    2 \sum_{i=1}^{n} x_{i}^{2} b_{1} &=2 \sum_{i=1}^{n} y_{i} x_{i} \\
    \hat{b}_{1} &=\frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sum_{i=1}^{n} x_{i}^{2}}
    \end{aligned}
    \]

    其中 \(\sum_{i=1}^n y_i x_i\) 是\(x,y\) 之間的協方差 (scaled by \(n\)), and \(\sum_{i=1}^n x_i^2\) 是\(x\)自身的方差

Least squares II: Projection

從其他角度去看這個最好的擬合線，就是幾何了，首先，直接把點投影到擬合線上，計算這個y軸上的差距作為誤差 這個誤差是垂直於x軸的，就像下面這幅圖一樣

\[\begin{aligned}
\left(\begin{array}{c}
\epsilon_{1} \\
\epsilon_{2} \\
\vdots \\
\epsilon_{n}
\end{array}\right) &=\left(\begin{array}{c}
y_{1} \\
y_{2} \\
\vdots \\
y_{n}
\end{array}\right)-\left(\begin{array}{c}
x_{1} \\
x_{2} \\
\vdots \\
z_{n}
\end{array}\right) b_{1} \\
& \epsilon=\mathbf{y}-\mathbf{x} b_{1}
\end{aligned}
\]



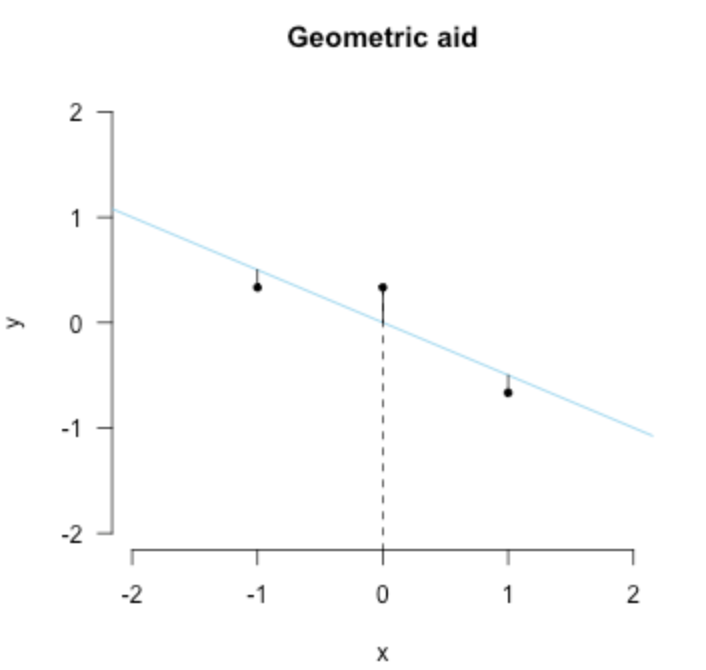
然後我們所希望的就是垂直於x軸的這個誤差很小，用數學來表示呢就是點乘加起來等於0，簡單版就是 \(\mathbf{x}^T \mathbf{\epsilon} = 0\)​​

\[\left(\begin{array}{llll}
x_{1} & x_{2} & \ldots & x_{n}
\end{array}\right)\left(\begin{array}{c}
\epsilon_{1} \\
\epsilon_{2} \\
\vdots \\
\epsilon_{n}
\end{array}\right)=0
\]

然後就又是最小二乘的方程式了：

\[\begin{aligned}
\mathbf{x}^{T} \epsilon &=0 \\
\mathbf{x}^{T}\left(\mathbf{y}-\mathbf{x} b_{1}\right) &=0 \\
\mathbf{x}^{T} \mathbf{x} b_{1} &=\mathbf{x}^{T} \mathbf{y} \\
b_{1} &=\frac{\mathbf{x}^{T} \mathbf{y}}{\mathbf{x}^{T} \mathbf{x}} \\
b_{1} &=\frac{\sum_{i=1}^{n} x_{i} y_{i}}{\sum_{i=1}^{n} x_{i}^{2}}
\end{aligned}
\]

咦 這是不是長的很像我們在方法一 優化里得到的結果，沒錯就是一模一樣的。

最後，可以注意到我們一直沒有對 \(b_0\) 進行估計，知道最小二乘結束後 \(b_0\)​ 還是未知的，所以最後我們處理的方式是 \(\bar y = b_0\)​ 也就是 \(y\)​ 的平均值。也正是因為這一事實，高斯曾經將高斯分布證明是誤差的分布。

「多好才是最好」 高斯, 拉普拉斯

雖然呢，最小二乘給出了怎樣去擬合出「最好」的曲線來縮小誤差，但是他並沒說明

  1. 誤差 \(\epsilon\)​​ 的隨機性
  2. 「多好才是最好」​ How good is best?

1809年是高斯將最小二乘放在了概率的角度去考慮。他做出了這樣一個假設：每一個誤差項 \(\epsilon_i\) 都是服從某個分布 \(\phi\) 的
利用這分布，當 \(\epsilon_i\) 很小時，\(\epsilon_i\)​​ 分布整體概率很大，而這個情況也就是觀測和預測值十分接近的時候。然後我們再進一步假設所有誤差分布都是 獨立同分布 ，他想找到能夠最大化概率 即最小化整體誤差

\[\Omega=\phi\left(\epsilon_{1}\right) \cdot \phi\left(\epsilon_{2}\right) \cdot \ldots \cdot \phi\left(\epsilon_{n}\right)=\prod_{i=1}^{n} \phi\left(\epsilon_{i}\right)
\]

所以呢，現在我們就要去找到這樣的一個分布 $\phi $。接著高斯大哥就發現我可以對 $\phi $ 做出一些說明，比如他一定是對稱的而且在等於誤差值=0的時候概率最大。接著他做出假設：平均值處應該就是能夠最好概括總結 \(n\) 個觀測值的地方 \((y_1,\dots,y_n)\) 所以，他假設最大化整個 \(\Omega\) 應該就和最小化整個均方誤差的和是一個性質

  • [x] 這裡有一點點不太能理解，He then assumed that the mean should be the best value for summarizing \(n\)​ measurements

    作者在注釋里寫了 the mean predicts the data best

  • [ ] 這裡還有一個 should lead to the same solution as minimizing the sum of squared errors when we have one unknown
    為啥是當我們有一個未知時？是指 \(b_0\) 嘛？

然後繞完這個圈後，高斯就證明最小二乘的誤差分布應該是這樣子的：

\[\phi\left(\epsilon_{i}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{1}{2 \sigma^{2}} \epsilon_{i}^{2}\right)
\]

其中 \(\sigma^{2}\)​ 是方差 (其實一開始高斯提出來的時候還不長這樣 最終為人所知的其實是Fisher修改了後方差後的版本) 這也就是為人所知的高斯分布，雖然呢 他一開始是Stigler’s law of eponomy，同時Karl Pearson也叫其正態分布，雖然他對此有絲絲後悔：

「Many years ago I called the Laplace–Gaussian curve the normal curve, which name, while it avoids an international question of priority, has the disadvantage of leading people to believe that all other distributions of frequency are in one sense or another 『abnormal』.」 (Pearson, 1920, p. 25)

分布圖如下：（雖然大家都知道了）



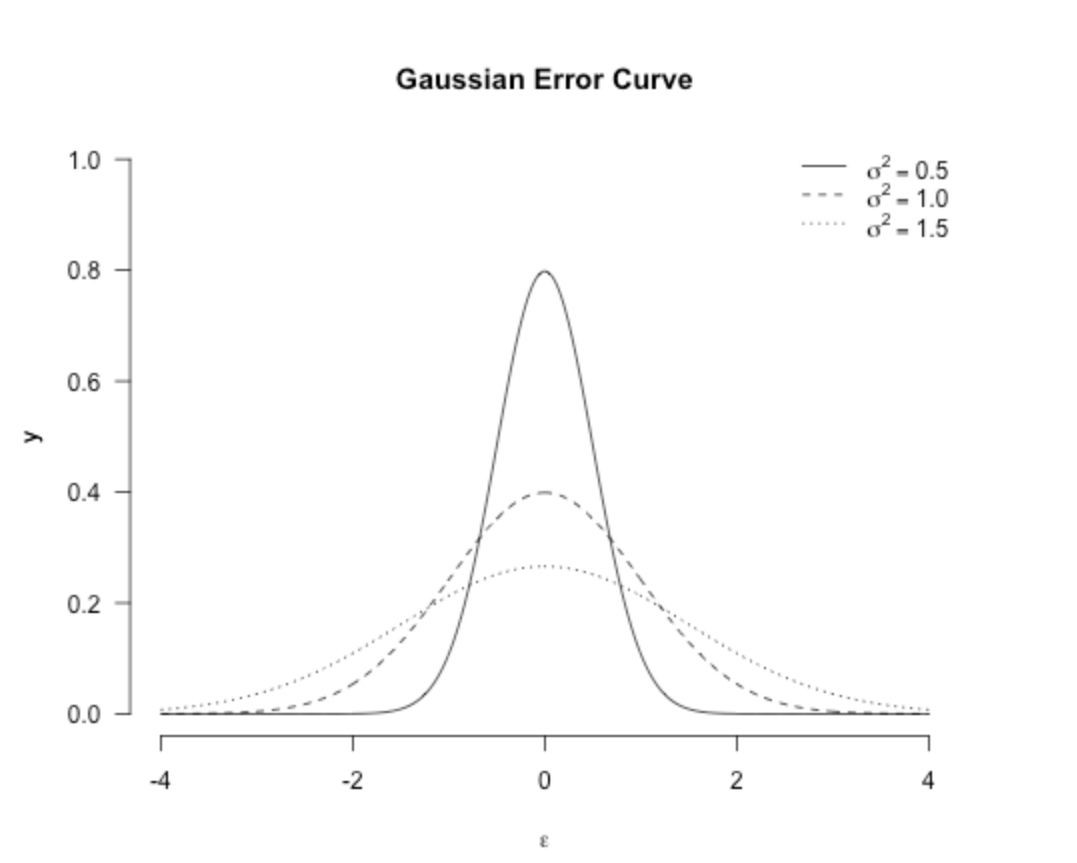
使用高斯分布後，我們的最大化問題就變成了這樣子：

\[\Omega=\prod_{i=1} \phi\left(\epsilon_{i}\right)=\prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{1}{2 \sigma^{2}} \epsilon_{i}^{2}\right)=\left(\frac{1}{\sqrt{2 \pi \sigma^{2}}}\right)^{n} \exp \left(-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n} \epsilon_{i}^{2}\right)
\]

注意：能使 \(\Omega\) 最大的值並不會隨其他的東西改變，比如添刪常數值，或者對其取對數log；

  1. \(-\sum_{i=1}^{n} \epsilon_{i}^{2}\) 這是我們想要最大化的東西

  2. 因為上面式子有負號，所以去掉負號的話是： \(\sum_{i=1}^{n} \epsilon_{i}^{2}\) ，同時最大化最小化這個

  3. 最後再看一遍這個 \(\sum_{i=1}^{n} \epsilon_{i}^{2}\)​ 也正是最小化均方誤差！

    我們並沒有因為分布遠離我們的初衷，到頭來分布概率還在朝著同一個目標

Pierre Simone de Laplace 沒錯就是拉普拉斯大哥在1810年注意到了高斯分布，然後給高斯誤差曲線再一次的證明：如果我們將誤差視為許多（微小）的擾動影響集合，這個集合將按照 中心極限定理正態分布

中心極限定理

我覺得這裡直接源自百度百科可能更快：

中心極限定理，是指概率論中討論隨機變數序列部分和分布漸近於正態分布的一類定理。這組定理是數理統計學和誤差分析的理論基礎，指出了大量隨機變數近似服從正態分布的條件。

前文中我們提到了散落的點是獨立同分布，在這個基礎上我們加的是 隨機性 ，也就是說有一串獨立同分布的隨機變數序列，如果此序列是有限的方差，那當 \(n\)​ 越大，此序列的平均值也就越大，而他也越接近正態分布；當 \(n \rightarrow \infin\)​ 平均值實際收斂到了正態分布

拉普拉斯意識到，如果將最小二乘問題中的誤差視為小影響的總和（即均值），那麼它們將呈正態分布。 這為最小二乘解提供了an elegant justification

舉個python程式的例子吧（原文是R語言的哈）

首先我們假設由 \(m=500\) 個獨立同分布(程式中分布為正態的) 生成的點，然後計算一個他們一起的誤差 \(\epsilon_i\)。假設我們有 \(n=200\) 組數據觀測，那麼就有200個獨立的誤差值，然後你可以可以發現這個誤差接近與高斯

import numpy as np
import matplotlib.pyplot as plt

n_error = 200
influence_one_error = 500

errors = list()

for i in range(n_error):
    errors.append(np.mean(np.random.uniform(-10, 10,influence_one_error)))

num_bins = 30

fig, ax = plt.subplots()

# the histogram of the data
n, bins, patches = ax.hist(errors, num_bins, density=True) # 誤差們直接的直方圖

# add a 'best fit' line
mu = 0
sigma = np.sqrt(20**2 / 12 ) / np.sqrt(influence_one_error) #隨意的 僅用來做表示
x = np.linspace(-1,1,num=1000)  # x軸的取值範圍
y = 1 / (sigma * pow(2 * np.pi, 0.5)) * np.exp(-((x - mu) ** 2) / (2 * sigma ** 2))  # 概率密度函數公式

ax.plot(x, y, 'r--')
ax.set_xlabel('Smarts')
ax.set_ylabel('Probability density')
ax.set_title('Central Limit Theorem')

# Tweak spacing to prevent clipping of ylabel
fig.tight_layout()
plt.show()

生成的圖：



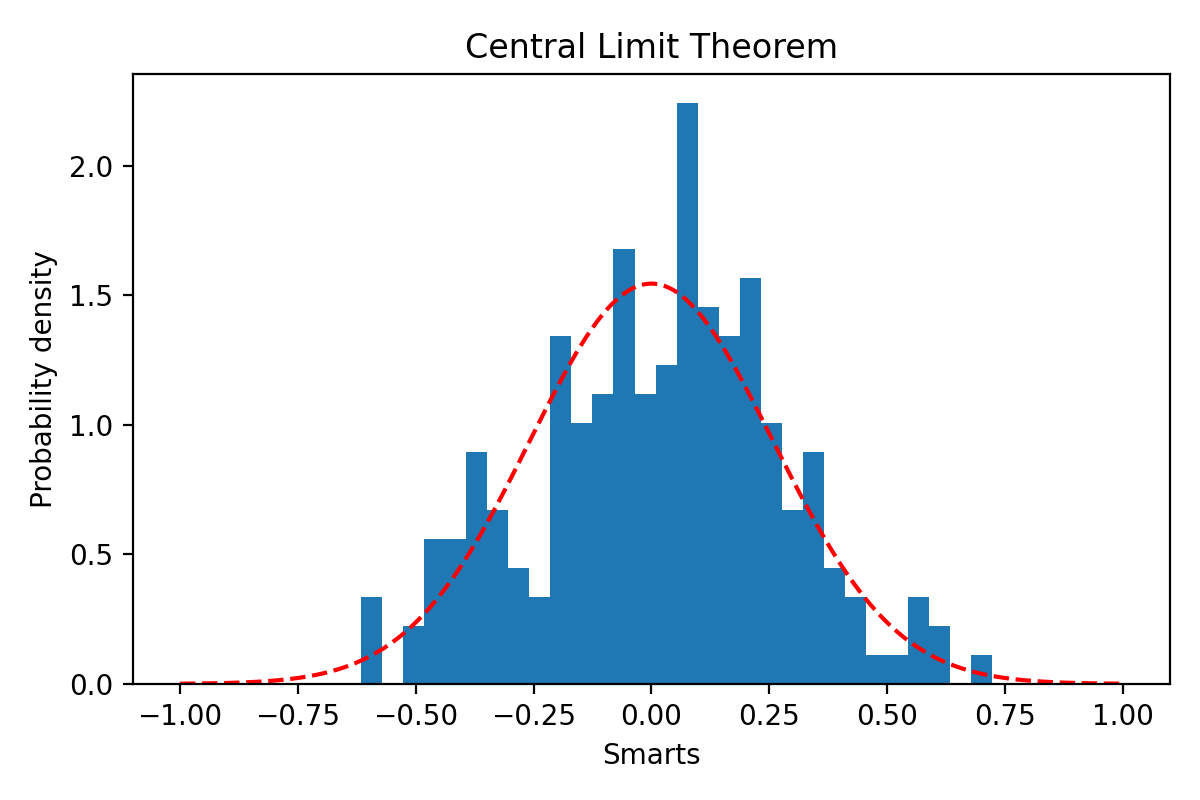
可能你還沒意識到這個有多棒，讓我幫你再來一次。首先我們是隨意的生成了500個正態分布(按定義來講 其他分布也OK 只要是他們一同屬於某一分布) 的數據，然後算平均值，計算他們自己內部的誤差是多少；而我們有200組這樣的數據，那麼我們就收集到了每組數據中自己的誤差，然後我們發現誤差間是屬於正態分布的。

線性回歸

最後我們再回到線性回歸這個問題，也就是之前提到的擬合。

高斯分布的一個特點是任何正態分布隨機變數的線性組合本身都是正態分布的。 我們可以將線性回歸問題寫成矩陣形式，這表明 y 是 x 的加權線性組合。 具體來說，如果我們有 n 個數據點，我們就有了一個由 n 個方程組成的系統，我們可以更簡潔地用矩陣表示法來寫

\[\begin{aligned}
\left(\begin{array}{c}
y_{1} \\
y_{2} \\
\vdots \\
y_{n}
\end{array}\right) &=\left(\begin{array}{cc}
1 & x_{1} \\
1 & x_{2} \\
\vdots & \vdots \\
1 & x_{n}
\end{array}\right) \cdot\left(\begin{array}{c}
b_{0} \\
b_{1}
\end{array}\right)+\left(\begin{array}{c}
\epsilon_{1} \\
\epsilon_{2} \\
\vdots \\
\epsilon_{n}
\end{array}\right) \\
\mathbf{y} &=\mathbf{X b}+\epsilon
\end{aligned}
\]

因為這種線性的關係，使得對誤差假設是正態分布，同時也為 \(\mathbf{y}\) 本身帶來了這一假設條件，也就是服從正態分布：

\[y_{i} \mid \mathbf{x}_{i} \sim \mathcal{N}\left(\mathbf{x}_{i}^{T} \mathbf{b}, \sigma^{2}\right)
\]

換句話說，每個點的 \(y_i\) 概率密度可以由這個公式給出：

\[\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{1}{2 \sigma^{2}}\left(y_{i}-\mathbf{x}_{i}^{T} \mathrm{~b}\right)^{2}\right)
\]

也就是下面這幅圖：



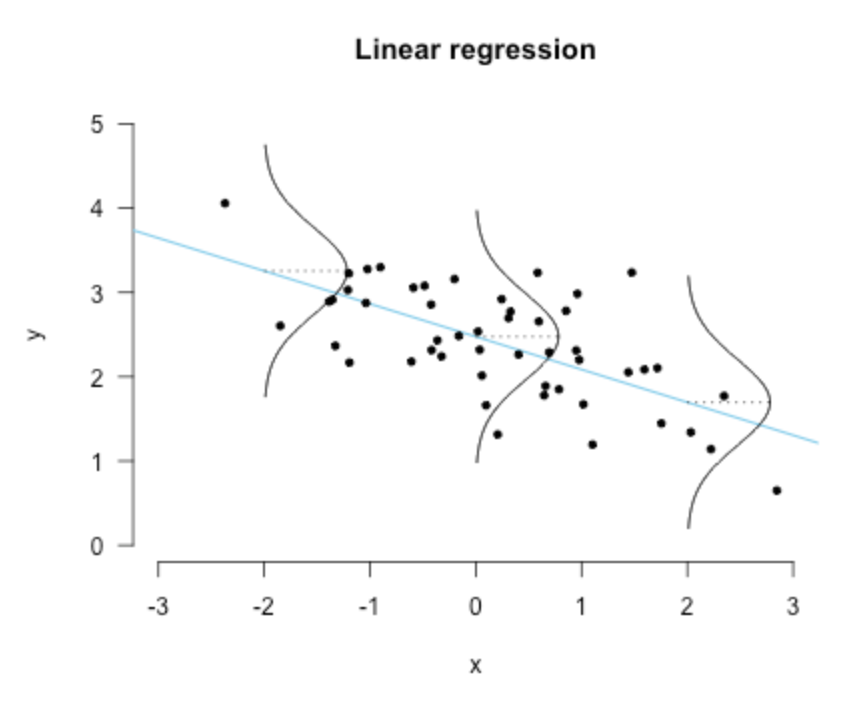
直觀上來看的話就是：誤差的方差越小，擬合的越好

後話 (相關性與回歸係數)

相關性並不意味著因果關係。 有些人認為線性回歸是一種因果模型，但是不是這樣的。

為了證明這一點，我們可以將簡單線性回歸中的回歸係數與相關性聯繫起來——它們僅在標準化上有所不同。

假設以均值為中心的數據，Pearson correlation的定義是：

\[r_{x y}=\frac{\sum_{i=1}^{n} x_{i} y_{i}}{\sqrt{\sum_{i=1}^{n} x_{i}^{2} \sum_{i=1}^{n} y_{i}^{2}}}
\]

注意這裡的相關性是對稱的，他並不取決於我們是x與y相關或是y與x相關。但是呢，在回歸中，我們使用x去預測y是這樣的：

\[b_{x y}=\frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sum_{i=1}^{n} x_{i}^{2}}
\]

但是我們如果是用y去預測x值，那係數就會變成這樣：

\[b_{y x}=\frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sum_{i=1}^{n} y_{i}^{2}} \neq b_{x y} \neq r_{x y}
\]

然而，通過對數據進行標準化，即通過將變數除以各自的標準差，回歸係數就成為了樣本相關性，即

\[\begin{aligned}
\frac{\partial L}{\partial b_{x y}} &=\frac{\partial}{\partial b_{x y}} \sum_{i=1}^{n}\left(\frac{y_{i}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2}}}-b_{x y} \frac{x_{i}}{\sqrt{\sum_{i=1}^{n} x_{i}^{2}}}\right)^{2} \\
&=\frac{\partial}{\partial b_{x y}}\left(\frac{\sum_{i=1}^{n} y_{i}^{2}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2}}}-2 b_{x y} \frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2} \sum_{i=1}^{n} x_{i}^{2}}}+b_{x y}^{2} \frac{\sum_{i=1}^{n} x_{i}^{2}}{\sum_{i=1}^{n} x_{i}^{2}}\right) \\
&=0-2 \frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2} \sum_{i=1}^{n} x_{i}^{2}}}+2 b_{x y} \\
2 b_{x y} &=2 \frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2} \sum_{i=1}^{n} x_{i}^{2}}} \\
b_{x y} &=\frac{\sum_{i=1}^{n} y_{i} x_{i}}{\sqrt{\sum_{i=1}^{n} y_{i}^{2} \sum_{i=1}^{n} x_{i}^{2}}}
\end{aligned}
\]

可以看到最後他又等於了 \(r_{xy}\) ，同時 這個標準化的回歸係數也可以通過乘以原始回歸係數來實現，即

\[b_s = b_{xy} \times \frac{\sqrt{\sum_{i=1}^n x_i^2}}{\sqrt{\sum_{i=1}^n y_i^2}} = \frac{\sum_{i=1}^n y_i x_i}{\sum_{i=1}^n x_i^2} \times \frac{\sqrt{\sum_{i=1}^n x_i^2}}{\sqrt{\sum_{i=1}^n y_i^2}} = \frac{\sum_{i=1}^n y_i x_i}{\sqrt{\sum_{i=1}^n y_i^2 \sum_{i=1}^n x_i^2}}
\]

同樣的對 \(b_{yx}\) 也是一樣的

\[b_s = b_{yx} \times \frac{\sqrt{\sum_{i=1}^n y_i^2}}{\sqrt{\sum_{i=1}^n x_i^2}} = \frac{\sum_{i=1}^n y_i x_i}{\sum_{i=1}^n y_i^2} \times \frac{\sqrt{\sum_{i=1}^n y_i^2}}{\sqrt{\sum_{i=1}^n x_i^2}} = \frac{\sum_{i=1}^n y_i x_i}{\sqrt{\sum_{i=1}^n y_i^2 \sum_{i=1}^n x_i^2}} \enspace
\]

VirMach 便宜 VPS

QNews

QNews