學C記錄（理解遞歸問題之漢諾塔）

• 2021 年 7 月 18 日
• 筆記

漢諾遊戲規則如下：

1、有三根相鄰的柱子，標號為A,B,C。

2、A柱子上從下到上按金字塔狀疊放著n個不同大小的圓盤。

3、現在把所有盤子一個一個移動到柱子B上，並且每次移動同一根柱子上都不能出現大盤子在小盤子上方。

程式要求：

輸入盤子個數，輸出完成步驟。

解決思路：

在完成題目前，首先應對遊戲規則和解題方法有所了解，此處借7k7k小遊戲中的漢諾塔（3個）演示。

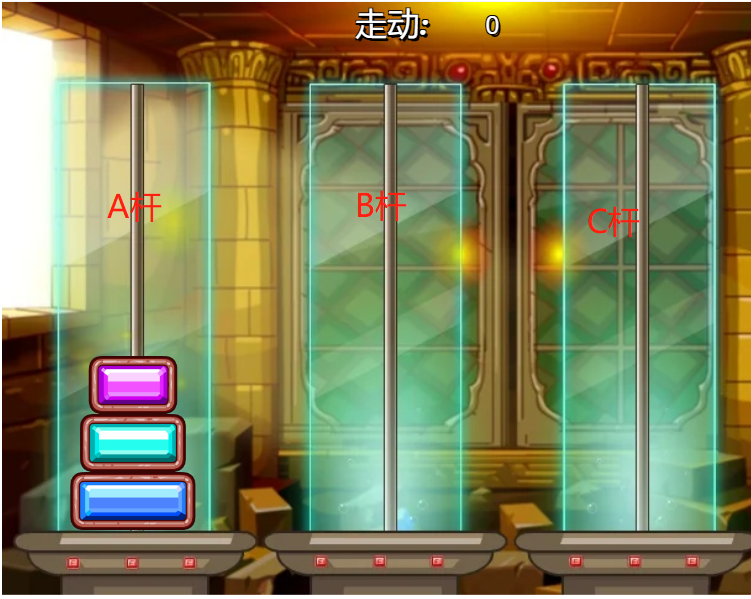
首先我們的目的是把A的三個盤子移到C處，所以首先應完成的便是把上兩個盤子放到B上，才能把第三個（最大的）盤子放到C，接著把B上的兩個放到C上。

所以這時我們發現，B的作用便是用來暫時存放除了最後一個的其他所有盤子，以便後續操作

所以我們可以設置x，y，z三個變數，分別表示初始盤子的位置，借放盤子的位置，最終完成的位置。

注意：x，y，z不一定與A，B，C始終一一對應！！！

A，B，C只是桿的名字！！！

因此程式的步驟：

1.當盤子等於一個，直接由x移到z。

2.當盤子大於一個（假設n個），先把n-1個盤子移到y，把第n個也就是最後一個大的，移到z。

3.把y上的盤子移到z。

剛開始我們把A，B，C對應x，y，z

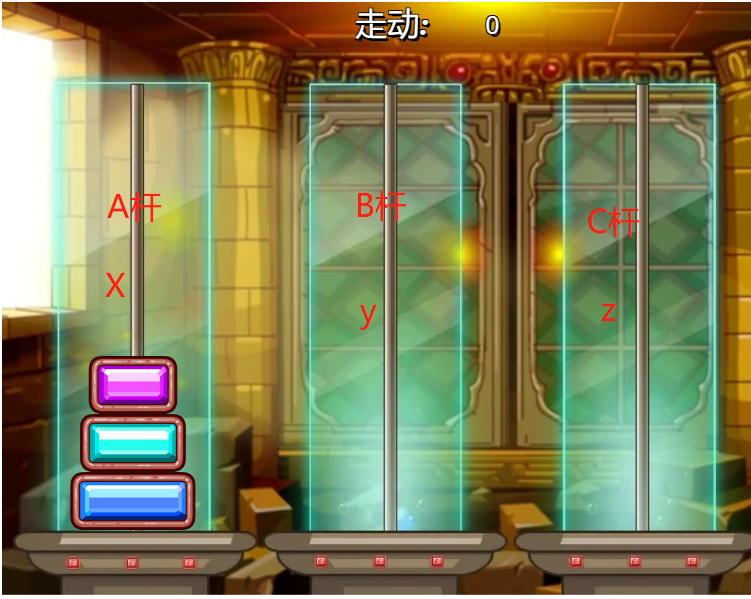
這時有個問題怎麼把x上的盤子移到y呢，這時我們就要轉換一下，先忽略掉第三個最大的盤的存在，把B桿看成目的地，C桿就變成y了（這就是為什麼說ABC與xyz不是一定對應的原因）

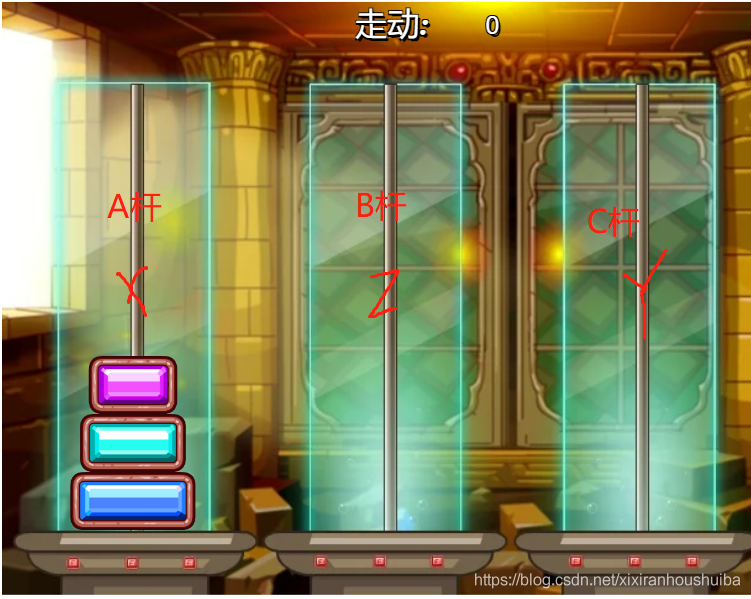
完成了上兩個轉移到B桿，便可以把A桿的最大盤移到C

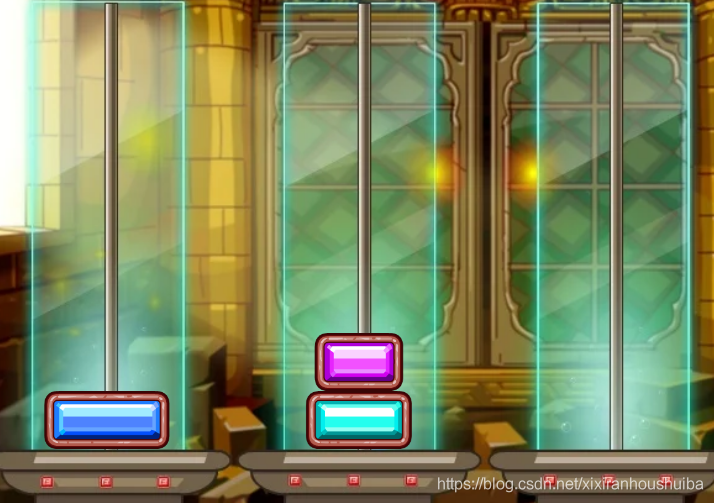
但當我們完成步驟2時，我們可以把原來的y也就是b桿看成是x（初始放盤子的地方），A桿看成y，C桿看成z（目的地），這時候便於剛開始步驟相似了
{{uploading-image-916509.png(uploading…)}}
所以重要的便是對盤子個數的判斷和對xyz的轉換
所以可以動手寫程式碼了，如下：

void Hanoi(int n, char x, char y, char z) //n為盤子個數
 {
	void move(char x, char z);
	if (1 == n)//當n等於1，執行步驟1
	 {
		move(x, z);
	} 
	else //當n不等於1，執行步驟2
	{
		Hanoi(n - 1, x, z, y);//把n-1從x移到y，所以原來的z便是現在借放的y，y同，所以反過來
		Hanoi(1, x, y, z);//完成上一步x移到上一步的y，就把最後的第n個從x移到z
		Hanoi(n - 1, y, x, z);//（此時的y有n-1個盤子，看成初始位置x），目的地還是z
	}
}

所以通過上面的操作便完成了盤子的所有移到

move函數的定義：

void move(char x, char z) 
{
	printf("%c ---> %c \n", x, z);
}

所以整個程式的程式碼如下：

int main() {
	int n = 0;
	void Hanoi(int n, char x, char y, char z);
	printf("請輸入所要移動的盤子的個數：");
	scanf("%d", &n);
	Hanoi(n, 'A', 'B', 'C');
}

void Hanoi(int n, char x, char y, char z) 
{
	void move(char x, char z);
	if (1 == n) {
		move(x, z);
	} else {
		Hanoi(n - 1, x, z, y);
		Hanoi(1, x, y, z);
		Hanoi(n - 1, y, x, z);
	}
}

void move(char x, char z) 
{
	printf("%c ---> %c \n", x, z);
}