noip模擬5[string·matrix·big·所駝門王的寶藏]
- 2021 年 6 月 7 日
- 筆記
怎麼說呢這一場考得還算可以呢
拿了120pts,主要是最後一個題靈光開竅,想起來是tarjan,然後勉勉強強拿了40pts,本來是可以拿滿分的,害
沒事考完了就要反思
這場考試我心態超好,從第一個題開始打暴力,一直打到第三題,嘿嘿自我感覺良好
不過我這個dfs的能力還是差了一點,得在磨練磨練!!!
要保持這種狀態先打暴力,再想正解!!!加油!!!

那就是正解環節了。。。。
T1 string
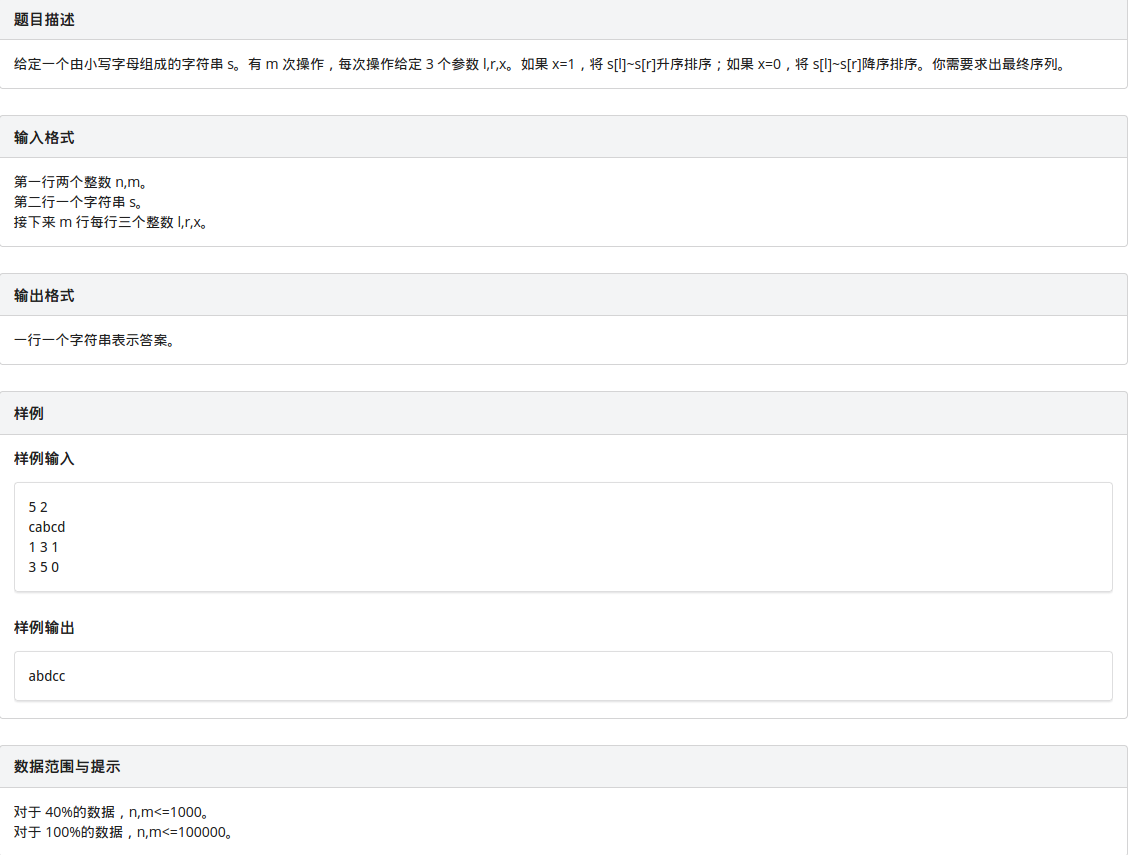
第一眼看到這個題,我說:::暴力有分了,看我10min把它A了,來來來。。。
我就上了
#include<bits/stdc++.h> using namespace std; #define re register int const int N=100005; int n,m; char ch[N]; signed main(){ scanf("%d%d",&n,&m); scanf("%s",ch+1); for(re i=1;i<=m;i++){ int l,r,x; scanf("%d%d%d",&l,&r,&x); if(x==1)sort(ch+l,ch+r+1); else sort(ch+l,ch+r+1,greater<char>()); } for(re i=1;i<=n;i++)printf("%c",ch[i]); }
sort大法好,直接拿到四十分,

於是就這樣我們成功的打完了第一題,用時:7min
不扯了,上正解
我們發現,上面的程式碼複雜度是m*n*logn的
所以我們盡量省去一個n,m是肯定在這裡的,搞不掉
大佬們說過一句話:
遇到線性問題時,我們要用線段樹;
遇到樹上的問題時,我們要用dfs序+線段樹;
那這個題我們就嘗試用線段樹來解決問題;
一開始是這麼想的,每個點就存這個點的字元就好了,後來發現我連線段樹是啥都不知道了,竟然只維護點。。。
在每個點上加一個桶(這名詞高大上吧!!就是開個數組,統計每個字元出現的次數)
然後就可以開開心心的用了
每一次排序,先把這個區間內的所有權值都提取出來,再一部分一部分的插入回去
一開始我覺得這樣會T的吧,但是好像沒有比這個更快的辦法了


#include<bits/stdc++.h> using namespace std; #define re register int #define mem(a) memset(a,0,sizeof(a)) const int N=100005; int n,m; char ch[N]; int num[N]; int now[27]; struct node{ #define ls x<<1 #define rs x<<1|1 int val[N*4][27]; int laz[N*4]; inline void pushup(int x){ for(re i=1;i<=26;i++) val[x][i]=val[ls][i]+val[rs][i]; } inline void pushdown(int x,int l,int r){ if(laz[x]){ int mid=l+r>>1; laz[ls]=laz[x]; laz[rs]=laz[x]; mem(val[ls]); mem(val[rs]); val[ls][laz[x]]=mid-l+1; val[rs][laz[x]]=r-mid; laz[x]=0; } } inline void build(int x,int l,int r){ if(l==r){ val[x][num[l]]=1; //cout<<(char)(num[l]+'a'-1)<<" "; return ; } int mid=l+r>>1; build(ls,l,mid); build(rs,mid+1,r); pushup(x); } inline void ins(int x,int l,int r,int ql,int qr,int c){ //if(ql>qr)return ; if(ql<=l&&r<=qr){ laz[x]=c; mem(val[x]); val[x][c]=r-l+1; return ; } pushdown(x,l,r); int mid=l+r>>1; if(ql<=mid)ins(ls,l,mid,ql,qr,c); if(qr>mid)ins(rs,mid+1,r,ql,qr,c); pushup(x); } inline void query(int x,int l,int r,int ql,int qr){ if(ql<=l&&r<=qr){ for(re i=1;i<=26;i++)now[i]+=val[x][i]; return ; } pushdown(x,l,r); int mid=l+r>>1; if(ql<=mid)query(ls,l,mid,ql,qr); if(qr>mid)query(rs,mid+1,r,ql,qr); } inline void dfs(int x,int l,int r){ if(l==r){ for(re i=1;i<=26;i++) if(val[x][i]){ printf("%c",i+'a'-1); break; } return ; } pushdown(x,l,r); int mid=l+r>>1; dfs(ls,l,mid); dfs(rs,mid+1,r); } #undef ls #undef rs }xds; signed main(){ scanf("%d%d",&n,&m); scanf("%s",ch+1); for(re i=1;i<=n;i++)num[i]=ch[i]-'a'+1; xds.build(1,1,n); for(re i=1;i<=m;i++){ int l,r,x; scanf("%d%d%d",&l,&r,&x); mem(now); xds.query(1,1,n,l,r); if(x==1){ for(re i=1;i<=26;i++){ if(!now[i])continue; xds.ins(1,1,n,l,l+now[i]-1,i); l+=now[i]; } } else{ for(re i=26;i>=1;i--){ if(!now[i])continue; xds.ins(1,1,n,l,l+now[i]-1,i); l+=now[i]; } } } xds.dfs(1,1,n); }
T1
過了這個題我覺得我又行了哈哈哈
T2 matrix
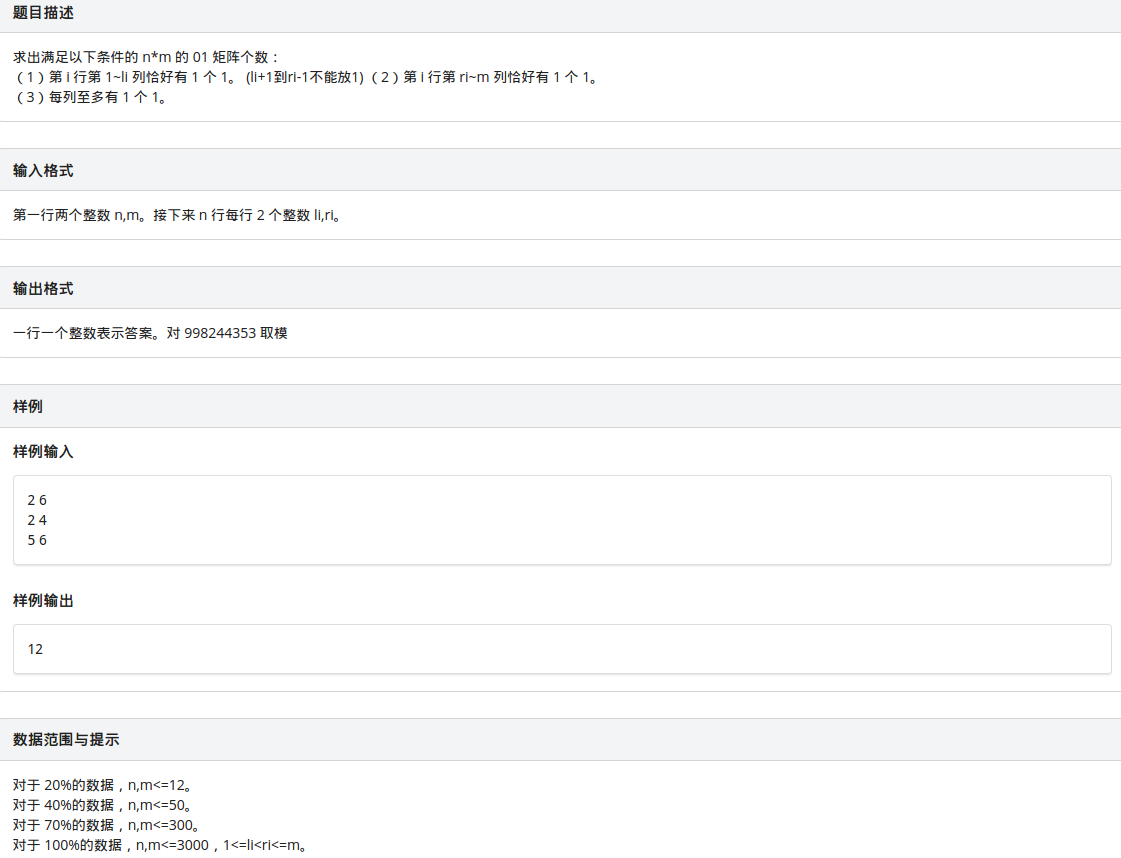
這個我在考場上的時候想了一個多小時,可就是沒想出來,一直在搗鼓我的組合數,就沒往dp上想
然後喜提0蛋一個;;;;;;
雖然我覺得我的思路還是沒有問題滴但他就是錯了
正解是dp誒
我們從左往右轉移,那麼我們發現左區間的方案數是可以直接通過A求得的
所以我們把重點放在右區間的轉移上,
我們設dp[i][j]表示,目前到了第i列,右區間內放了j個1,左區間的方案在每一次轉移的時候乘上就好了
那麼我們就先考慮左區間的轉移:
(等會我們先處理一個數據,這裡l[i]表示左區間的終點(就是輸入的l)小於等於i的個數,r[i]表示右區間的起點(就是輸入的r)小於等於i的個數)
1、l[i]==l[i-1]那麼這個時候沒有新的1要放進去,所以直接由上一個狀態轉移 dp[i][j]+=dp[i-1][j];
2、l[i]>l[i-1]這個時候乘方案數了,此時一共放了j+l[i-1]個1,所以還剩下i-j-l[i-1]列可以放1,要放進去l[i]-l[i-1]個點所以乘上A(i-j-l[i-1],l[i]-l[i-1])
哎呀呀,上面那個太麻煩了,直接乘不就好了嘛,反正l[i]==l[i-1]的時候A返回的是1,,,都一樣都一樣啦
再考慮右區間的轉移:就按照上面說的,不用分開算了
右區間一定一定從dp[i-1][j-1]轉移過來因為只能加一個1嘛,這沒問題吧,再乘上目前有多少個點可以用來放1,乘上A
所以dp[i][j]+=dp[i-1][j-1]*(r[i]-(j-1))*A(A同上)
因為最後一定會佔滿所有的矩陣,所以答案就是dp[m][n];
程式碼來了


#include<bits/stdc++.h> using namespace std; #define re register int const int N=3005; const int mod=998244353; int n,m; int f[N],b[N]; int l[N],r[N]; int jc[N],inv[N]; int dp[N][N],ans; int ksm(int x,int y){ int ret=1; while(y){ if(y&1)ret=1ll*ret*x%mod; x=1ll*x*x%mod; y>>=1; } return ret; } int A(int x,int y){ //cout<<jc[x]<<" "<<inv[x-y]<<endl; return 1ll*jc[x]*inv[x-y]%mod; } signed main(){ scanf("%d%d",&n,&m); for(re i=1;i<=n;i++){ scanf("%d%d",&f[i],&b[i]); l[f[i]]++; r[b[i]]++; } dp[0][0]=1;jc[0]=1; for(re i=1;i<=m;i++){ l[i]+=l[i-1]; r[i]+=r[i-1]; jc[i]=1ll*jc[i-1]*i%mod; } inv[0]=1;inv[m]=ksm(jc[m],mod-2); //cout<<inv[m]<<endl; for(re i=m-1;i>=1;i--){ inv[i]=1ll*inv[i+1]*(i+1)%mod; } for(re i=1;i<=m;i++){ for(re j=0;j<=r[i];j++){ //cout<<dp[i][j]<<endl; if(l[i]==l[i-1])dp[i][j]=(1ll*dp[i][j]+dp[i-1][j])%mod; else dp[i][j]=1ll*dp[i-1][j]*A(i-j-l[i-1],l[i]-l[i-1])%mod; if(j) dp[i][j]=(dp[i][j]+1ll*dp[i-1][j-1]*(r[i]-(j-1))%mod*A(i-j-l[i-1],l[i]-l[i-1])%mod)%mod; } } printf("%d",dp[m][n]); }
T2

(心情愉悅,粘張圖片)
所以T3 big
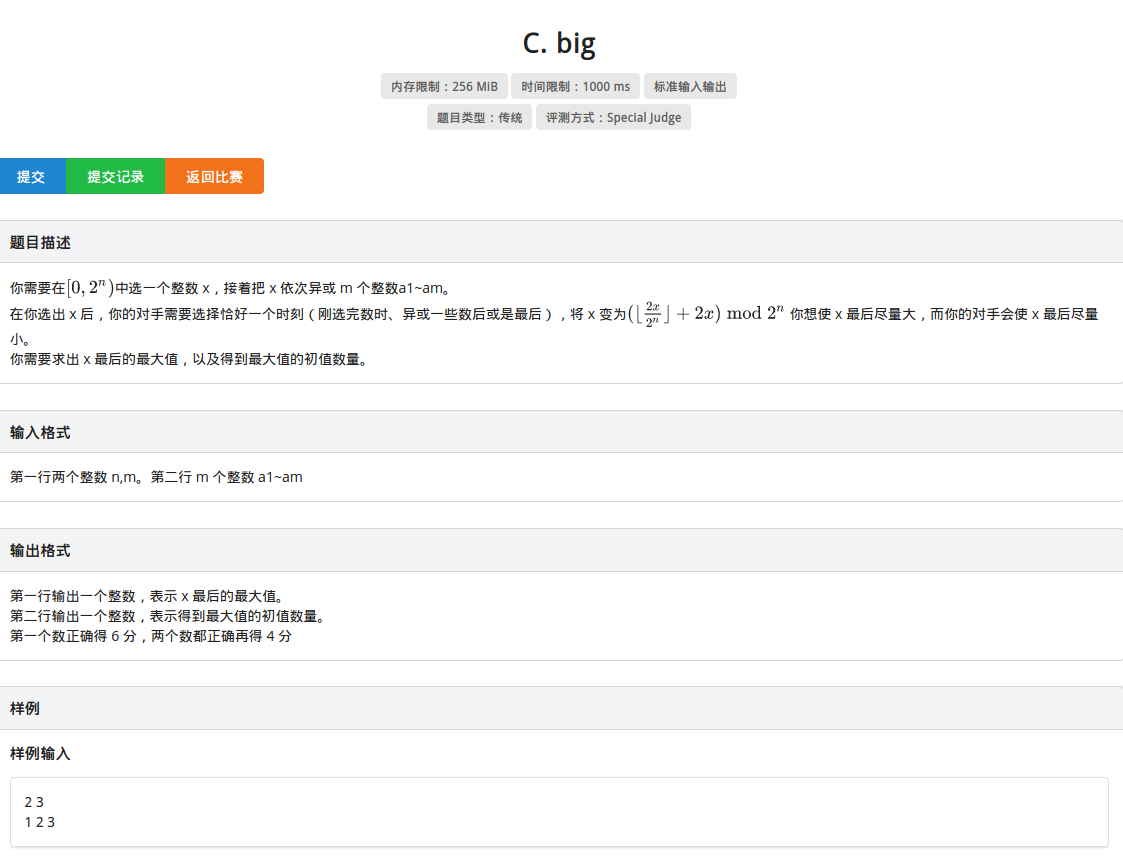
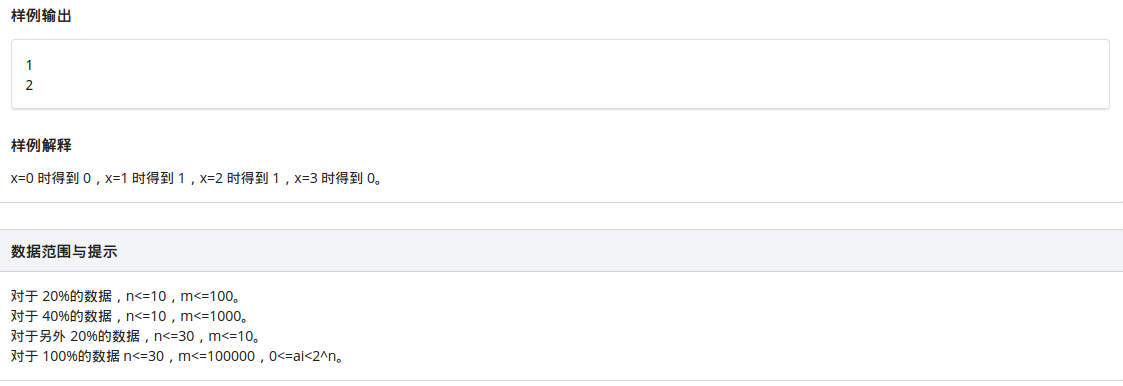
那麼這個題我暴力拿到了40pts,下面是暴力程式碼,分別求取前綴和,然後枚舉
#include<bits/stdc++.h> using namespace std; #define re register int const int N=1e5+10; int n,m; int a[N],fro[N]; int maxn,ans,sum; signed main(){ scanf("%d%d",&n,&m); for(re i=1;i<=m;i++){ scanf("%d",&a[i]); fro[i]=fro[i-1]^a[i]; } for(re i=0;i<(1<<n);i++){ int tmp;maxn=(1<<n); for(re j=0;j<=m;j++){ tmp=i; tmp^=fro[j]; tmp=(2*tmp/(1<<n)+2*tmp)%(1<<n); tmp^=fro[m]^fro[j]; if(tmp<maxn)maxn=tmp; } if(maxn==ans)sum++; if(maxn>ans)ans=maxn,sum=1; } printf("%d\n%d",ans,sum); }

全部都是TLE啊
然後正解其實是trie樹
你發現他給你的那一長串,就是把x循環左移
就是1100000變成1000001,就是左移一位,然後最高位的放到最低位去,循環節就是n
然後左移的操作就成為一個分界點
可以發現如果將一個數左移一下,就相當於把他自己和那些要異或的數都左移以為
然後我們枚舉每個分界點,的到了一個數組存的就是可以通過一步異或得到答案的數組
把它們放到trie樹上
然後如果有一位既能取到0,也能取到1,那這一位就是一個無效位,不會對答案作出任何貢獻,因為無論你拿出來的數是啥我總能把這一位變成0
所以這樣就可以統計最大值和數目了


#include<bits/stdc++.h> using namespace std; #define re register int const int N=100005; int n,m; int a[N],fro[N],beh[N]; int b[N]; struct trie{ int v,son[2]; }tr[N*50]; int seg; int an; long long su; void ins(int x){ int u=0; for(re i=n-1;i>=0;i--){ int tmp=1&(x>>i); //cout<<tmp<<" "; if(!tr[u].son[tmp]) tr[u].son[tmp]=++seg; u=tr[u].son[tmp]; } //cout<<endl; } void dfs(int x,int dep,int ans,long long sum){ dep--; if(dep==-1){ if(an<ans)an=ans,su=1; else if(an==ans)su++; } //cout<<x<<" "<<dep<<" "<<tr[x].son[0]<<" "<<tr[x].son[1]<<endl; if(!tr[x].son[0]&&!tr[x].son[1])return ; if(!tr[x].son[0]||!tr[x].son[1]){ ans+=(1<<dep); if(tr[x].son[0])dfs(tr[x].son[0],dep,ans,sum); else dfs(tr[x].son[1],dep,ans,sum); return ; } dfs(tr[x].son[0],dep,ans,sum); dfs(tr[x].son[1],dep,ans,sum); } signed main(){ scanf("%d%d",&n,&m); for(re i=1;i<=m;i++){ scanf("%d",&a[i]); fro[i]=fro[i-1]^a[i]; } for(re i=1;i<=m;i++){ int t=a[i]>>(n-1); a[i]=a[i]<<1; a[i]|=t; b[i]=b[i-1]^a[i]; } for(re i=0;i<=m;i++){ b[i]^=fro[m]^fro[i]; //cout<<b[i]<<endl; ins(b[i]); } dfs(0,n,0,1); printf("%d\n%lld",an,su); }
T3
這麼看的話,這個題也不算難
T4 所駝門王的寶藏


說實話這題真水,水暴了
就一個tarjan縮點
+臨接表+map+記憶化搜索


#include<bits/stdc++.h> using namespace std; #define re register int #define pa pair<int,int> const int N=2000100; int n,r,c; struct node{ int x,y,typ; }mea[N]; struct edge{ int nxt,id; }xe[N*2],ye[N*2]; int hrp,xea[N],yea[N]; map<pa,int> zym; int zx[10]={0,-1,-1,-1,0,0,1,1,1}; int zy[10]={0,-1,0,1,-1,1,-1,0,1}; int to[N*2],nxt[N*2],head[N],rp; void add_edg(int x,int y){ to[++rp]=y; nxt[rp]=head[x]; head[x]=rp; } int dfn[N],low[N],cnt; int pos[N],val[N],col; int du[N],dp[N]; stack<int> q; void dfs(int x){ dfn[x]=low[x]=++cnt; q.push(x); for(re i=head[x];i;i=nxt[i]){ int y=to[i]; if(!dfn[y]){ dfs(y); low[x]=min(low[x],low[y]); } else if(!pos[y]){ low[x]=min(low[x],low[y]); } } if(dfn[x]==low[x]){ pos[x]=++col; val[col]++; while(x!=q.top()&&!q.empty()){ int y=q.top();//cout<<y<<" "; q.pop(); pos[y]=col; val[col]++; } q.pop(); } } int t_[N*2],n_[N*2],h_[N*2],r_; void add_ed(int x,int y){ t_[++r_]=y; n_[r_]=h_[x]; h_[x]=r_; } int vis[N],ans; void dfs_(int x){ if(dp[x]>val[x])return ; dp[x]=val[x]; for(re i=h_[x];i;i=n_[i]){ int y=t_[i]; dfs_(y); dp[x]=max(dp[x],dp[y]+val[x]); } } signed main(){ scanf("%d%d%d",&n,&r,&c); for(re i=1;i<=n;i++){ scanf("%d%d%d",&mea[i].x,&mea[i].y,&mea[i].typ); xe[++hrp].id=i;xe[hrp].nxt=xea[mea[i].x];xea[mea[i].x]=hrp; ye[hrp].id=i;ye[hrp].nxt=yea[mea[i].y];yea[mea[i].y]=hrp; pa a=(pa){mea[i].x,mea[i].y};zym[a]=i; } for(re i=1;i<=n;i++){ int x=mea[i].x,y=mea[i].y,typ=mea[i].typ; if(typ==1){ for(re j=xea[x];j;j=xe[j].nxt) if(i!=xe[j].id)add_edg(i,xe[j].id); } else if(typ==2){ for(re j=yea[y];j;j=ye[j].nxt) if(i!=ye[j].id)add_edg(i,ye[j].id); } else{ for(re j=1;j<=8;j++){ pa a=(pa){x+zx[j],y+zy[j]}; if(zym[a])add_edg(i,zym[a]); } } } for(re i=1;i<=n;i++) if(!dfn[i])dfs(i); for(re i=1;i<=n;i++){ for(re j=head[i];j;j=nxt[j]) if(pos[i]!=pos[to[j]]) add_ed(pos[i],pos[to[j]]),du[pos[to[j]]]++;//cout<<pos[to[j]]<<" "; } for(re i=col;i>=1;i--){ if(du[i]==0){ dfs_(i); ans=max(ans,dp[i]); } } printf("%d",ans); }
T3
完結撒花!!!!!



