DARTS:基於梯度下降的經典網路搜索方法,開啟端到端的網路搜索 | ICLR 2019
DARTS是很經典的NAS方法,它的出現打破了以往的離散的網路搜索模式,能夠進行end-to-end的網路搜索。由於DARTS是基於梯度進行網路更新的,所以更新的方向比較準確,搜索時間相當於之前的方法有很大的提升,CIFAR-10的搜索僅需要4GPU days。
來源:曉飛的演算法工程筆記 公眾號
論文: DARTS: Differentiable Architecture Search

Introduction
目前流行的神經網路搜索方法大都是對離散的候選網路進行選擇,而DARTS則是對連續的搜索空間進行搜索,並根據驗證集的表現使用梯度下降進行網路結構優化,論文的主要貢獻如下:
- 基於bilevel優化提出創新的gradient-based神經網路搜索方法DARTS,適用於卷積結構和循環結構。
- 通過實驗表明gradient-based結構搜索方法在CIFAR-10和PTB數據集上都有很好的競爭力。
- 搜索性能很強,僅需要少量GPU days,主要得益於gradient-based優化模式。
- 通過DARTS在CIFAR-10和PTB上學習到的網路能夠轉移到大數據集ImageNet和WikiText-2上。
Differentiable Architecture Search
Search Space
DARTS的整體搜索框架跟NASNet等方法一樣,通過搜索計算單元(cell)的作為網路的基礎結構,然後堆疊成卷積網路或者循環網路。計算單元是個有向無環圖,包含N個節點的有序序列,每個節點x^{(i)}代表網路的中間資訊(如卷積網路的特徵圖),邊代表對x^{(i)}的操作o^{(i,j)}。每個計算單元有兩個輸入和一個輸出,對於卷積單元,輸入為前兩層的計算單元的輸出,對於循環網路,輸入則為當前step的輸入和前一個step的狀態,兩者的輸出均為將中間節點的所有輸出進行合併操作。每個中間節點的計算基於前面所有的節點:
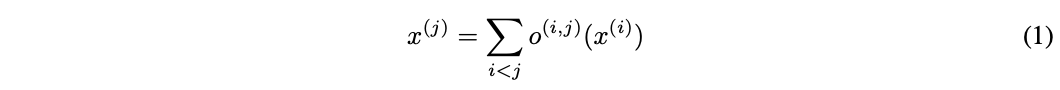
這裡包含一個特殊的zero操作,用來指定兩個節點間沒有連接。DARTS將計算單元的學習轉換為邊操作的學習,整體搜索框架跟NASNet等方法一樣,本文主要集中在DARTS如何進行gradient-based的搜索。
Continuous Relaxation and Optimization
讓O為候選操作集,每個操作代表應用於x^{(i)}的函數o(\cdot),為了讓搜索空間連續化,將原本的離散操作選擇轉換為所有操作的softmax加權輸出:
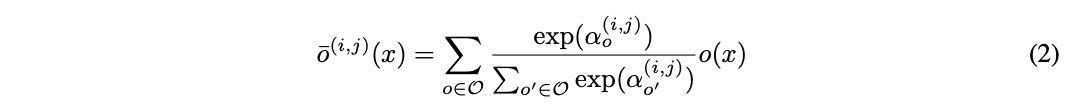
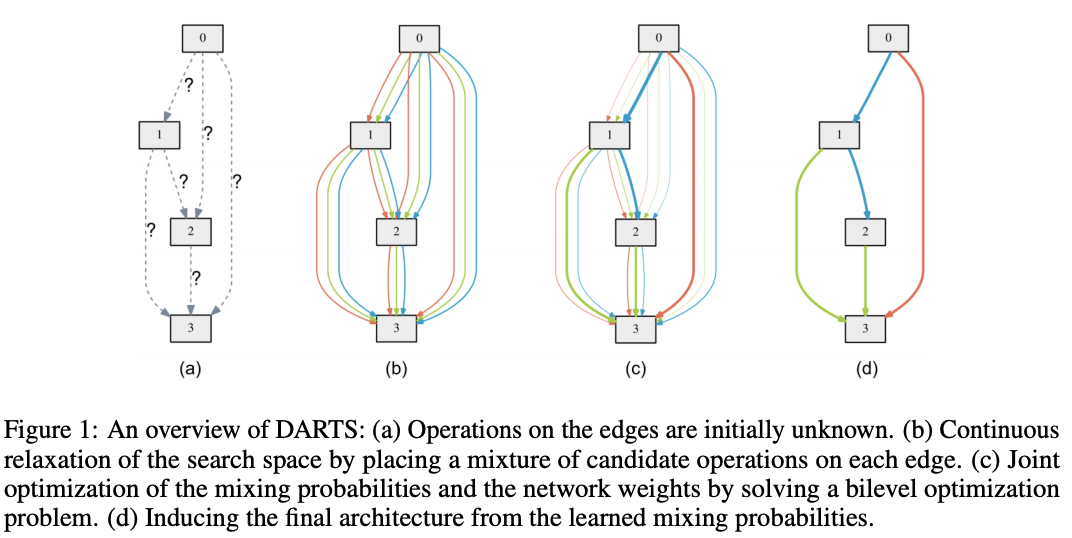
節點(i,j)間的操作的混合權重表示為維度|O|的向量\alpha^{(i,j)},整個架構搜索則簡化為學習連續的值\alpha=\{\alpha^{(i, j)}\},如圖1所示。在搜索的最後,每個節點選擇概率最大的操作o^{(i,j)}=argmax_{o\in O}\alpha^{(i,j)}_o代替\bar{o}^{(i,j)},構建出最終的網路。
在簡化後,DARTS目標是夠同時學習網路結構\alpha和所有的操作權值w。對比之前的方法,DARTS能夠根據驗證集損失使用梯度下降進行結構優化。定義\mathcal{L}_{train}和\mathcal{L}_{val}為訓練和驗證集損失,損失由網路結構\alpha和網路權值w共同決定,搜索的最終目的是找到最優的\alpha^{*}來最小化驗證集損失\mathcal{L}_{val}(w^{*}, \alpha^{*}),其中網路權值w^{*}則是通過最小化訓練損失w^{*}=argmin_w \mathcal{L}_{train}(w, \alpha^{*})獲得。這意味著DARTS是個bilevel優化問題,使用驗證集優化網路結構,使用訓練集優化網路權重,\alpha為上級變數,w為下級變數:
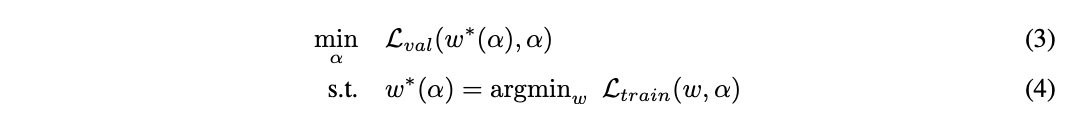
Approximate Architecture Gradient
公式3計算網路結構梯度的開銷是很大的,主要在於公式4的內層優化,即每次結構的修改都需要重新訓練得到網路的最優權重。為了簡化這一操作,論文提出了提出了簡單的近似的改進:
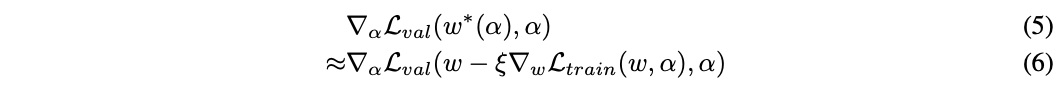
w表示當前的網路權重,\xi是內層優化單次更新的學習率,整體的思想是在網路結構改變後,通過單次訓練step優化w來逼近w^{(*)}(\alpha),而不是公式3那樣需要完整地訓練直到收斂。實際當權值w為內層優化的局部最優解時(\nabla_{w}\mathcal{L}_{train}(w, \alpha)=0),公式6等同於公式5\nabla_{\alpha}\mathcal{L}_{val}(w, \alpha)。

迭代的過程如演算法1,交替更新網路結構和網路權重,每次的更新都僅使用少量的數據。根據鏈式法則,公式6可以展開為:
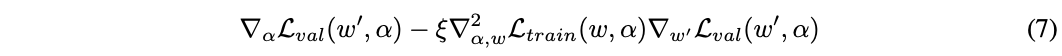
w^{‘}=w – \xi \nabla_w \mathcal{L}_{train}(w, \alpha),上述的式子的第二項計算的開銷很大,論文使用有限差分來近似計算,這是論文很關鍵的一步。\epsilon為小標量,w^{\pm}=w\pm \epsilon \nabla_{w^{‘}} \mathcal{L}_{val}(w^{‘}, \alpha),得到:
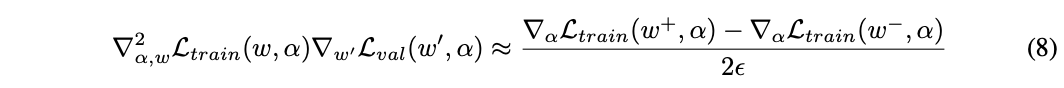
計算最終的差分需要兩次正向+反向計算,計算複雜度從O(|\alpha| |w|)簡化為O(|\alpha|+|w|)。
-
First-order Approximation
當\xi=0時,公式7的二階導會消失,梯度由\nabla_{\alpha}\mathcal{L}(w, \alpha)決定,即認為當前權值總是最優的,直接通過網路結構修改來優化驗證集損失。\xi=0能加速搜索的過程,但也可能會帶來較差的表現。當\xi=0時,論文稱之為一階近似,當\xi > 0時,論文稱之為二階近似。
Deriving Discrete Architectures
在構建最終的網路結構時,每個節點選取來自不同節點的top-k個響應最強的非zero操作,響應強度通過\frac{exp(\alpha^{(i,j)_o})}{\sum_{o^{‘}\in O}exp(\alpha^{(i,j)}_{o^{‘}})}計算。為了讓搜索的網路性能更好,卷積單元設置k=2,循環單元設置k=1。過濾zero操作主要讓每個節點有足夠多的輸入,這樣才能與當前的SOTA模型進行公平比較。
Experiments and Results
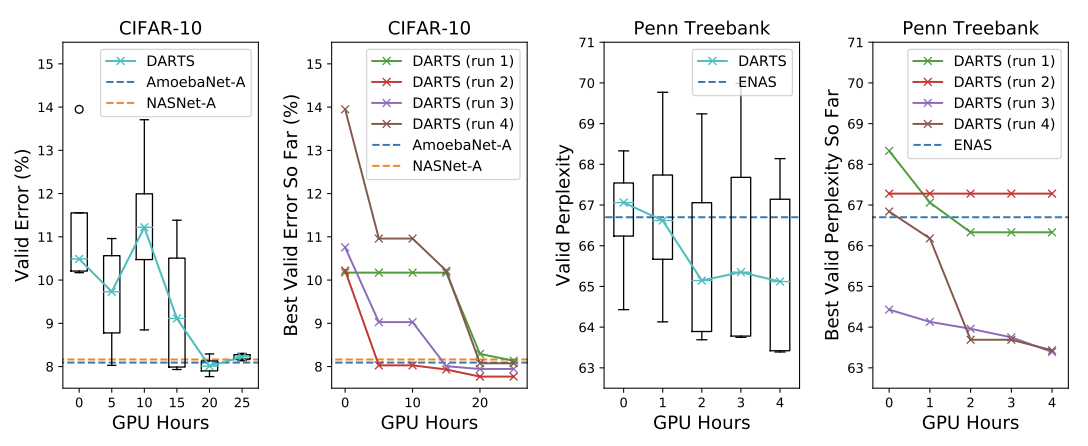
搜索耗時,其中run代表多次搜索取最好的結果。
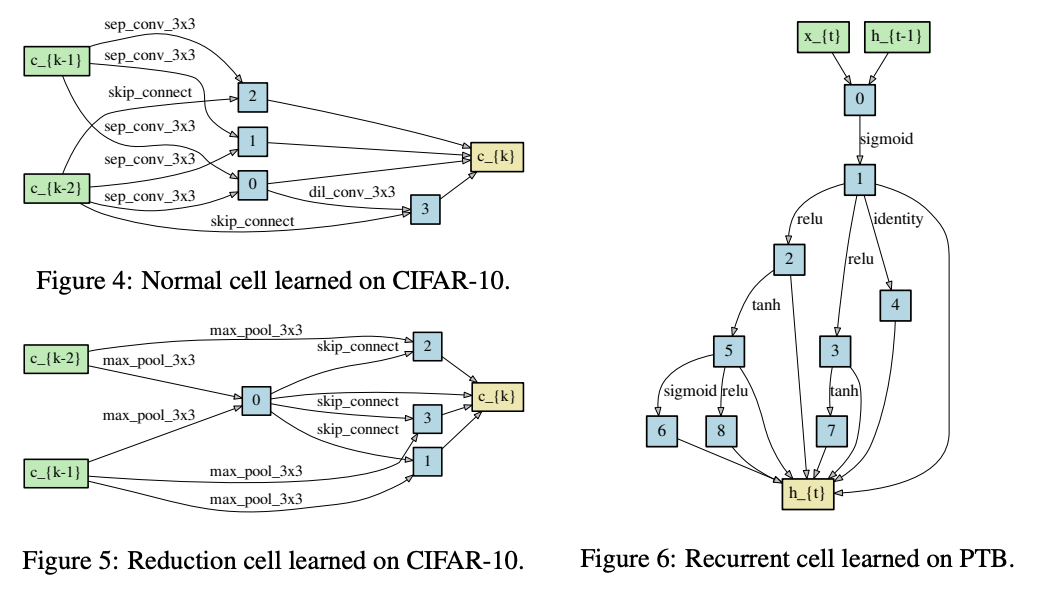
搜索到的結構。
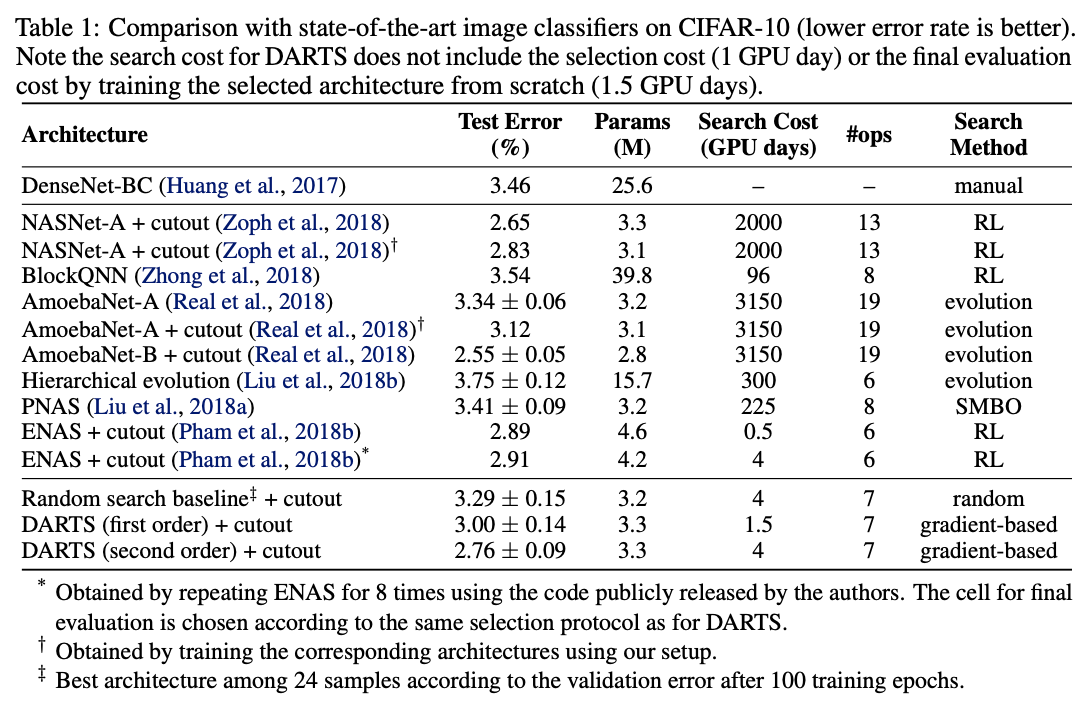
CIFAR-10上的性能對比。
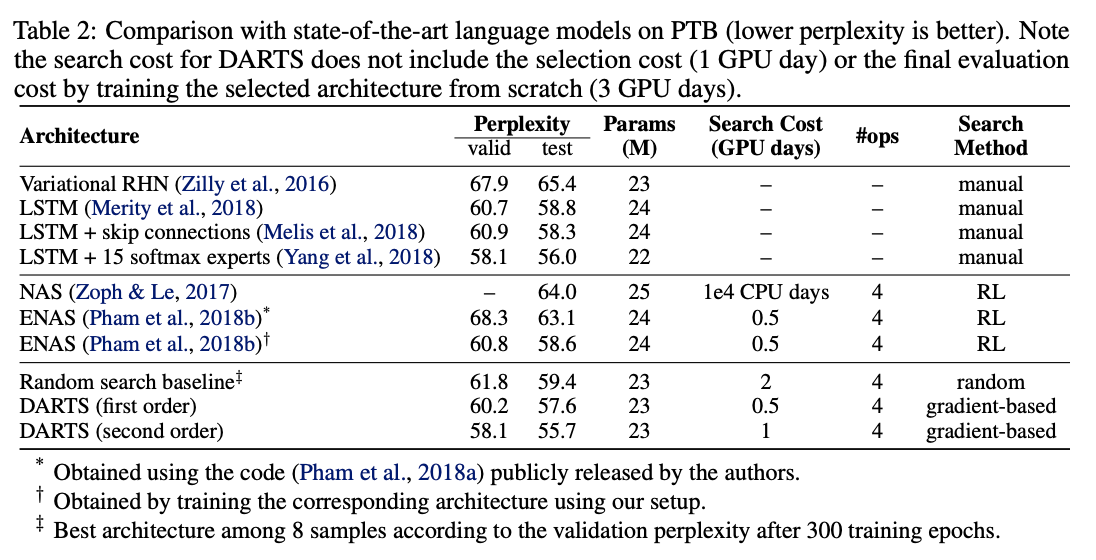
PTB上的性能對比。
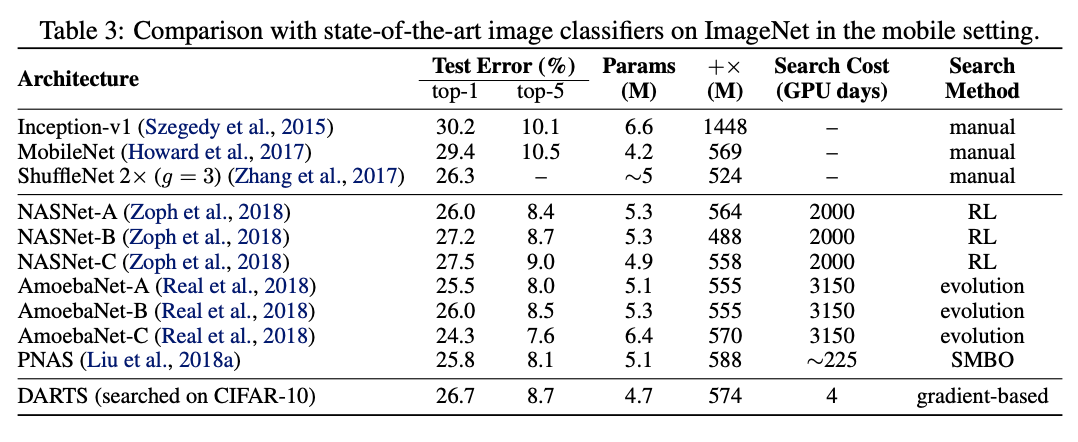
遷移到ImageNet上的性能對比。
Conclustion
DARTS是很經典的NAS方法,它的出現打破了以往的離散的網路搜索模式,能夠進行end-to-end的網路搜索。由於DARTS是基於梯度進行網路更新的,所以更新的方向比較準確,搜索時間相當於之前的方法有很大的提升,CIFAR-10的搜索僅需要4GPU days。
如果本文對你有幫助,麻煩點個贊或在看唄~
更多內容請關注 微信公眾號【曉飛的演算法工程筆記】



