做一個logitic分類之鳶尾花數據集的分類
- 2019 年 10 月 3 日
- 筆記
做一個logitic分類之鳶尾花數據集的分類
Iris 鳶尾花數據集是一個經典數據集,在統計學習和機器學習領域都經常被用作示例。數據集內包含 3 類共 150 條記錄,每類各 50 個數據,每條記錄都有 4 項特徵:花萼長度、花萼寬度、花瓣長度、花瓣寬度,可以通過這4個特徵預測鳶尾花卉屬於(iris-setosa, iris-versicolour, iris-virginica)中的哪一品種。
首先我們來載入一下數據集。同時大概的展示下數據結構和數據摘要。
import numpy as np import pandas as pd import matplotlib.pyplot as plt data = pd.read_csv('./data/iris.csv') print(data.head()) print(data.info()) print(data['Species'].unique()) Unnamed: 0 Sepal.Length Sepal.Width Petal.Length Petal.Width Species 0 1 5.1 3.5 1.4 0.2 setosa 1 2 4.9 3.0 1.4 0.2 setosa 2 3 4.7 3.2 1.3 0.2 setosa 3 4 4.6 3.1 1.5 0.2 setosa 4 5 5.0 3.6 1.4 0.2 setosa <class 'pandas.core.frame.DataFrame'> RangeIndex: 150 entries, 0 to 149 Data columns (total 6 columns): Unnamed: 0 150 non-null int64 Sepal.Length 150 non-null float64 Sepal.Width 150 non-null float64 Petal.Length 150 non-null float64 Petal.Width 150 non-null float64 Species 150 non-null object dtypes: float64(4), int64(1), object(1) memory usage: 7.2+ KB None ['setosa' 'versicolor' 'virginica']通過上述數據的簡單摘要,我們可以得到鳶尾花一共有三類:
- setosa
- versicolor
- virginica
我們分別用0,1,2來表示[‘setosa’ ‘versicolor’ ‘virginica’]
整理
首先,我們對數據集進行一個簡單的整理。我們需要把分類替換成0,1,2
其次,我們把數據集分成兩個分類,一個用來訓練我們的logitic演算法的參數,另外一個用來測試我們的訓練的結果
以下是程式碼:
# 數值替換 data.loc[data['Species']=='setosa','Species']=0 data.loc[data['Species']=='versicolor','Species']=1 data.loc[data['Species']=='virginica','Species']=2 print(data) Unnamed: 0 Sepal.Length Sepal.Width Petal.Length Petal.Width Species 0 1 5.1 3.5 1.4 0.2 0 1 2 4.9 3.0 1.4 0.2 0 2 3 4.7 3.2 1.3 0.2 0 3 4 4.6 3.1 1.5 0.2 0 4 5 5.0 3.6 1.4 0.2 0 .. ... ... ... ... ... ... 145 146 6.7 3.0 5.2 2.3 2 146 147 6.3 2.5 5.0 1.9 2 147 148 6.5 3.0 5.2 2.0 2 148 149 6.2 3.4 5.4 2.3 2 149 150 5.9 3.0 5.1 1.8 2 [150 rows x 6 columns]#分割訓練集和測試集 train_data = data.sample(frac=0.6,random_state=0,axis=0) test_data = data[~data.index.isin(train_data.index)] train_data = np.array(train_data) test_data = np.array(test_data) train_label = train_data[:,5:6].astype(int) test_label = test_data[:,5:6].astype(int) print(train_label[:1]) print(test_label[:1]) train_data = train_data[:,1:5] test_data = test_data[:,1:5] print(np.shape(train_data)) print(np.shape(train_label)) print(np.shape(test_data)) print(np.shape(test_label))[[2]] [[0]] (90, 4) (90, 1) (60, 4) (60, 1)我們需要把label編程1ofN的樣式
經過上述兩步的操作,我們可以看到數據集被分成兩個部分。我們接下來對數據進行logitic分類。
train_label_onhot = np.eye(3)[train_label] test_label_onhot = np.eye(3)[test_label] train_label_onhot = train_label_onhot.reshape((90,3)) test_label_onhot = test_label_onhot.reshape((60,3))print(train_label_onhot[:3])[[0. 0. 1.] [0. 1. 0.] [1. 0. 0.]]分類
思路
我選選擇先易後難的方法來處理這個問題:
如果我們有兩個分類0或者1的話,我們需要判斷特徵值X(N維)是否可以歸為某個分類。我們的步驟如下:
- 初始化參數w(1,N)和b(1)
- 計算 (z = sum_{i=0}^{n}w*x + b)
- 帶入(sigma)函數得到(hat{y}=sigma(z))
現在有多個分類, 我們就需要使用one-to-many的方法去計算。簡單的理解,在本題中,一共有3個分類。我們需要計算(hat{y}_1)來表明這個東西是分類1或者不是分類1的概率 (hat{y}_2)是不是分類2的概率,(hat{y}_3)是不是分類3的概率。然後去比較這三個分類那個概率最大,就是哪個的概率。
比較屬於哪個概率大的演算法,我們用softmat。就是計算(exp(hat{y}_1)),(exp(hat{y}_2)),(exp(hat{y}_3)),然後得到屬於三個分類的概率分別是
- p1=(frac{exp(hat{y}_1)}{sum_{i=0}{3}(hat{y}_i)})
- p1=(frac{exp(hat{y}_2)}{sum_{i=0}{3}(hat{y}_i)})
- p1=(frac{exp(hat{y}_3)}{sum_{i=0}{3}(hat{y}_i)})
我們根據上述思想去計算一條記錄,程式碼如下:
def sigmoid(s): return 1. / (1 + np.exp(-s)) w = np.random.rand(4,3) b = np.random.rand(3) def get_result(w,b): z = np.matmul(train_data[0],w) +b y = sigmoid(z) return y y = get_result(w,b) print(y) [0.99997447 0.99966436 0.99999301]上述程式碼是我們只求一條記錄的程式碼,下面我們給他用矩陣化修改為一次計算全部的訓練集的(hat{y})
def get_result_all(data,w,b): z = np.matmul(data,w)+ b y = sigmoid(z) return y y=get_result_all(train_data,w,b) print(y[:10])[[0.99997447 0.99966436 0.99999301] [0.99988776 0.99720719 0.9999609 ] [0.99947512 0.98810796 0.99962362] [0.99999389 0.99980632 0.999999 ] [0.9990065 0.98181945 0.99931113] [0.99999094 0.9998681 0.9999983 ] [0.99902719 0.98236513 0.99924728] [0.9999761 0.99933525 0.99999313] [0.99997542 0.99923594 0.99999312] [0.99993082 0.99841774 0.99997519]]接下來我們要求得一個損失函數,來計算我們得到的參數和實際參數之間的偏差,關於分類的損失函數,請看這裡
單個分類的損失函數如下:
[loss=−sum_{i=0}^{n}[y_ilnhat{y}_i+(1−y_i)ln(1−hat{y}_i)]]
損失函數的導數求法如下
當 (y_i=0)時
w的導數為:
[ frac{dloss}{dw}=(1-y_i)*frac{1}{1-hat{y}_i}*hat{y}_i*(1-hat{y}_i)*x_i ]
化簡得到
[ frac{dloss}{dw}=hat{y}*x_i=(hat{y}-y)*x_i ]
b的導數為
[ frac{dloss}{db}=(1-y_i)*frac{1}{1-hat{y}_i}*hat{y}_i*(1-hat{y}_i) ]
化簡得到
[frac{dloss}{db}=hat{y}-y]
當(y_i)=1時
w的導數
[ frac{dloss}{dw}=-yi*frac{1}{hat{y}}*hat{y}(1-hat{y})*x_i ]
化簡
[ frac{dloss}{dw}=(hat{y}-1)*x_i=(hat{y}-y)*x_i ]
b的導數
[frac{dloss}{dw}=hat{y}-y]
綜合起來可以得到
[ frac{dloss}{dw}=sum_{i=0}^{n}(hat{y}-y)*x_i ]
[ frac{dloss}{db}=sum_{i=0}^{n}(hat{y}-y) ]
我們只需要根據以下公式不停的調整w和b,就是機器學習的過程
[w=w-learning_rate*dw]
[b=b-learning_rate*db]
下面我們來寫下程式碼:
learning_rate = 0.0001 def eval(data,label, w,b): y = get_result_all(data,w,b) y = y.argmax(axis=1) y = np.eye(3)[y] count = np.shape(data)[0] acc = (count - np.power(y-label,2).sum()/2)/count return acc def train(step,w,b): y = get_result_all(train_data,w,b) loss = -1*(train_label_onhot * np.log(y) +(1-train_label_onhot)*np.log(1-y)).sum() dw = np.matmul(np.transpose(train_data),y - train_label_onhot) db = (y - train_label_onhot).sum(axis=0) w = w - learning_rate * dw b = b - learning_rate * db return w, b,loss loss_data = {'step':[],'loss':[]} train_acc_data = {'step':[],'acc':[]} test_acc_data={'step':[],'acc':[]} for step in range(3000): w,b,loss = train(step,w,b) train_acc = eval(train_data,train_label_onhot,w,b) test_acc = eval(test_data,test_label_onhot,w,b) loss_data['step'].append(step) loss_data['loss'].append(loss) train_acc_data['step'].append(step) train_acc_data['acc'].append(train_acc) test_acc_data['step'].append(step) test_acc_data['acc'].append(test_acc) plt.plot(loss_data['step'],loss_data['loss']) plt.show() plt.plot(train_acc_data['step'],train_acc_data['acc'],color='red') plt.plot(test_acc_data['step'],test_acc_data['acc'],color='blue') plt.show() print(test_acc_data['acc'][-1])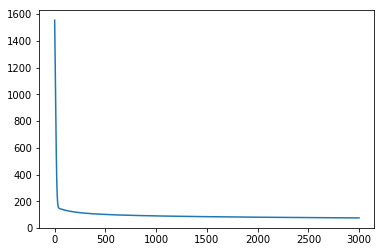 [png]
[png]
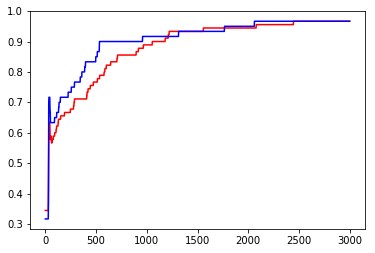
0.9666666666666667從上述運行結果中來看,達到了96.67%的預測準確度。還不錯!
