LeetCode-42. 接雨水 (hard) - ⎝⎛CodingNote.cc ⎞⎠

LeetCode—42. 接雨水 (hard)

2021 年 5 月 8 日
筆記
JAVA, leetcode, 刷題, 每日一題

題目：42. 接雨水

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之後能接多少雨水。

示例：

輸入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
輸出：6
解釋：上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。

第一種解法：暴力破解，一列一列算

思路

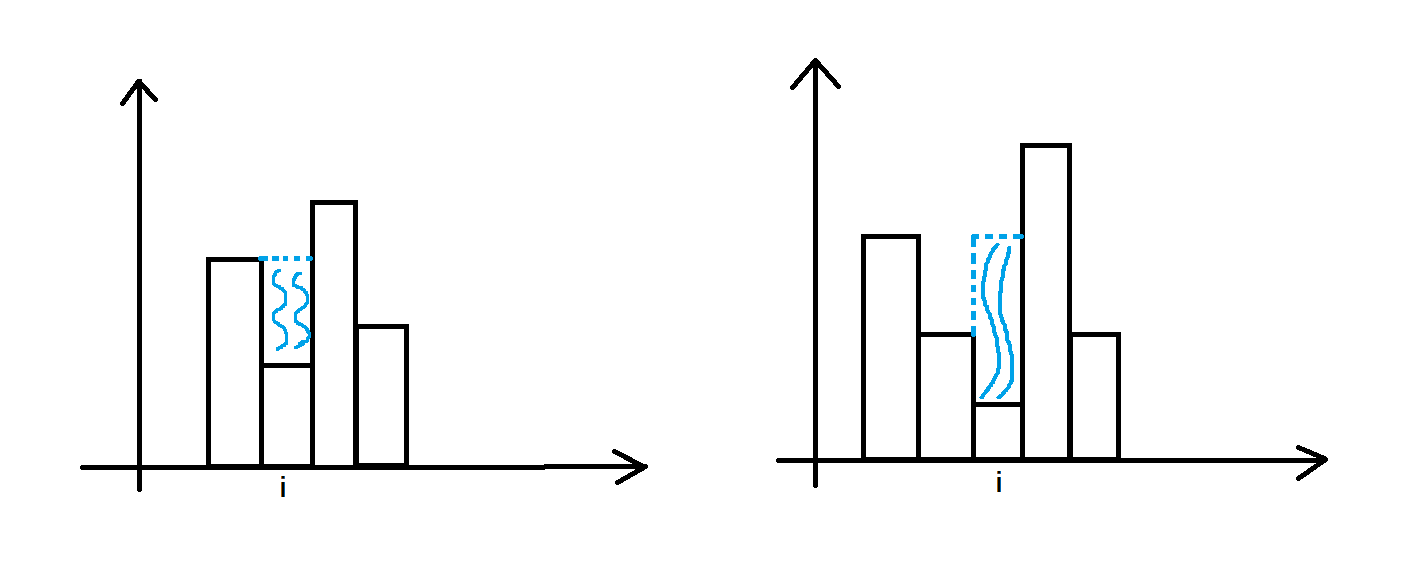
使用雙層循環，在遍歷每一根柱子的同時，求出第i柱子左右兩邊高度最高的柱子分別是多少，然後根據兩邊高度最高柱子中較低的那根柱子去求出第i根柱子最多能接多少雨水。看下圖做參考理解

步驟

外層循環遍歷每根柱子
1. 內層嵌套循環①，求第i根柱子左邊高度最高的柱子，記錄下來max_left
2. 內層嵌套循環②，求第 i根柱子右邊高度最高的柱子，記錄下來max_right
3. max_left與max_right進行比較，算出兩邊最高的柱子中較低的一根，因為它類似於木桶效應，桶中水的高度總是由較低的木板的高度決定
4. 如果此時兩邊柱子中較低的一根柱子比當前遍歷的柱子i要高，就說明這根柱子能盛放住雨水
5. 柱子i能盛放的雨水量就等於它兩邊最高柱子中較低的一根柱子的高度減去當前柱子的高度，得出結果將其加入到計算的雨水總量中
返回能接雨水的總量

程式碼

根據程式碼進一步理解

// 暴力破解，按列求
public int trap(int[] height) {
    int sum = 0;
    int len = height.length;
    for (int i = 1; i < len - 1; i++) {
        int max_left = 0;
        int max_right = 0;
        int min_height = 0;
        //求元素左邊最高的柱子
        for (int j = i - 1; j >= 0; j--) {
            if (height[j] > max_left)
                max_left = height[j];
        }
        
        //求元素右邊最高的柱子
        for (int k = i + 1; k < len; k++) {
            if (height[k] > max_right)
                max_right = height[k];
        }
        //求出較低的柱子
        min_height = Math.min(max_left,max_right);
        //比較計算
        if (min_height > height[i])
            sum += min_height - height[i];
    }
    return sum;
}

優化

外層循環是從左到右遍歷每根柱子，而內層求左側最高的柱子的時候又從左到右循環，顯然是有冗餘的,我們可以使用max_left直接標記左側最高的柱子，每次只需要比較max_left與前一根柱子的高度大小，而不需要再進行一次遍歷

程式碼如下，改動很小，只將原來求元素左邊最高的柱子的for循環改變為if語句

// 暴力破解優化
public int trap(int[] height) {
    int sum = 0;
    int max_left = 0;
    for (int i = 1; i < height.length - 1; i++) {
        //求元素左邊最高的柱子
        if (height[i-1] > max_left)
            max_left = height[i-1];
        
        //求元素右邊最高的柱子
        int max_right = 0;
        for (int k = i + 1; k < height.length; k++) {
            if (height[k] > max_right)
                max_right = height[k];
        }
        //求出較低的柱子
        int min_height = Math.min(max_left,max_right);
        //比較計算
        if (min_height > height[i])
            sum += min_height - height[i];
    }
    return sum;
}

參照這個思路，該如何標記遍歷時右側最高的柱子呢？

那麼我們就來看下一種解法思路

第二種解法：動態規劃求解

思路

我們可以創建兩個數組分別記錄每根柱子左側最高的柱子以及右側最高的柱子

就像我們第一種解法最後的優化思路一樣，第i根柱子左側最高的柱子就等於第i-1根柱子與第i-1根柱子前最高的柱子中較高的一根，也就是max_left[i] = Math.max(max_left[i-1],height[i-1])

那第i根柱子右側最高的柱子應該怎樣算？

我們可以倒序遍歷，從右往左遍歷柱子，用數組記錄下來第i根柱子右側最高的柱子是那根，類似的，第i+1根柱子與第i+1根柱子右邊較高的一根就是第i根柱子右側高度最高的柱子，也就是max_right[i] = Math.max(max_right[i+1], height[i+1])

要謹慎對待邊界問題

程式碼

    // 動態規劃求解
    public int trap3(int[] height) {
        int sum = 0;
        int[] max_left = new int[height.length];
        int[] max_right = new int[height.length];

        // 每根柱子對應的左邊最高的柱子 (注: 並沒有使用上一解法的優化做法，而是使用純種的動態規劃，循序漸進，希望可以便於理解)
        for (int i = 1; i < height.length - 1; i++) {
            max_left[i] = Math.max(max_left[i-1],height[i-1]);
        }

        // 每根柱子對應的右邊最高的柱子
        for (int i = height.length - 2; i >= 0; i--) {
            max_right[i] = Math.max(max_right[i+1], height[i+1]);
        }

        int min_height = 0;
        for (int i = 1; i < height.length; i++) {
            min_height = Math.min(max_left[i],max_right[i]);
            if (min_height > height[i])
                sum += min_height - height[i];
        }
        return sum;
    }

進行優化的思路

其實，我們在使用數組的過程中只使用了一個值，這點我們在第一種解法的優化思路中已經說過了，所以說我們只需要各用一個值來記錄左右兩邊的最高柱子就可以，但是循環是從左往右遍歷的，所以左側最高柱子max_left好記錄，而右側我們又想降低空間複雜度，不使用數組來記錄最高柱子，那我們應該如何來解決呢？往下看

第三種解法：雙指針解決

思路

我們可以使用雙指針來很好的解決這個問題，使用left和right分別指向數組兩端

我們重新理一下思路，這裡不太好想

一根柱子能盛放的水的多少，取決於它左右兩邊最高的柱子中較低的一根

在遍歷的過程中，從左往右遍歷我們能知道max_left是確定的，從右往左遍歷我們能知道max_right是確定的，而只要我們確定了這兩個值中較小的值是多少，我們就可以確定這根柱子能盛多少水，那麼另一個較大的值無論多大都不會影響結果。

所以我們可以從兩端分別進行遍歷，當第left-1根柱子高度小於第right+1根柱子高度時left向右移，我們計算第left根柱子能盛水多少，當第left-1根柱子大於第right+1根柱子高度時right向左移，計算第right根柱子能盛水多少。

我們可以試著這樣去理解，從一開始，如果第left-1根柱子高度比第right+1根柱子低，那麼max_left就會一直比max_right低，直到通過left指針向右不斷移動到了一個使得第left-1根柱子的高度比第right+1根柱子的高度高的情況，那麼此時max_left就比max_right更高，我們就可以將right指針向左移。。。這樣一次一次通過left-1與right+1的比較以及左右指針的交替使用，我們就可以逐一確定所有柱子能夠盛放水的多少

雙指針的解法非常巧妙，大家請多思考

程式碼

// 雙指針求解
public int trap(int[] height) {
    int sum = 0;
    int max_left = 0;
    int max_right = 0;
    int left = 1;
    int right = height.length - 2;
    
    for (int i = 1; i < height.length - 1; i++) {
        if (height[left-1] < height[right+1]) {
            max_left = Math.max(max_left,height[left-1]);
            int min = max_left;
            if (min > height[left])
                sum += min - height[left];
            left++;
        }else {
            max_right = Math.max(max_right,height[right+1]);
            int min = max_right;
            if (min > height[right])
                sum += min - height[right];
            right--;
        }
    }
    
    return sum;
}

第四種解法：單調棧解法

除了使用雙指針進行優化，我們還可以使用特殊的數據結構來解決

思路

積水存在的原因是什麼？

當這根柱子的兩側有比它更高的柱子存在，這根柱子所在的地方就形成了低洼，就能夠存儲水源

我們從左側開始遍歷，如果一個元素比它的棧頂元素小，就入棧

反之，如果遍歷到一個元素，此元素比棧頂元素大，就說明棧頂元素兩側可能形成了高度差，棧頂元素彈出棧，此元素與新的棧頂元素進行判斷與計算，直到此元素不大於此時棧頂元素，然後此元素入棧。

程式碼

// 單調遞減棧解法
public int trap1(int[] height) {
    int sum = 0;
    int cur = 0;  //指向的是當前元素
    Deque<Integer> stack = new ArrayDeque<>();
    while (cur < height.length) {
        while (!stack.isEmpty() && height[cur] > height[stack.peek()]) {
            //棧頂元素出棧並賦值給 h
            int h = stack.pop();
            //棧頂元素出棧之後再次判斷棧是否為空，如果為空，直接進行下次循環
            if (stack.isEmpty())
                break;
            // 判斷當前元素與此時棧頂之間的距離
            int distance = cur - stack.peek() - 1;
            // 求出當前元素與此時棧頂元素中高度較小的一邊
            int min_h = Math.min(height[cur],height[stack.peek()]);
            // 求出之前棧頂也就是 h 所能盛放水的多少
            sum += distance * (min_h - height[h]);
        }
        stack.push(cur);
        cur++;
    }
    return sum;
}

Tags: JAVA leetcode 刷題每日一題