P7518 & 省選聯考2021 寶石
這是一篇極其簡單連像我這樣省三參加不了省選的蒟蒻都能看懂的題解
前置知識: 倍增LCA 二分 棧 題意
PS:這是一篇完全面向初學者的題解,會非常細,大佬請無視
沒有思路的時候, 我們往往可以從簡單的情況下手, 比如一條鏈
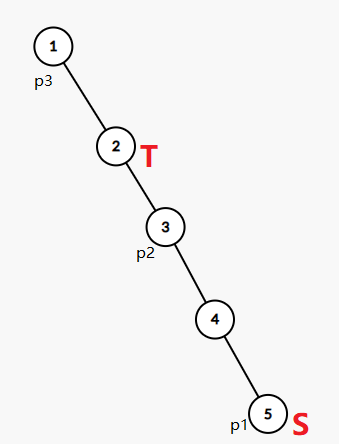
我們記Pi為第i個需要搜集的寶石, S為起點, T為終點。
不妨先假設我們有一條鏈, 每個節點指向下一個要搜集的寶石(向上), 也就p1指向向上最近的一個p2, p2指向p3(為什麼是最近,讀者可自行思考)
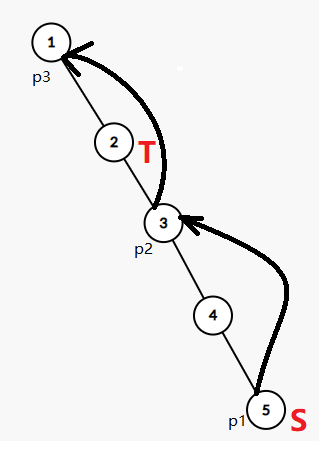
這個時候S是第一個要搜集的寶石, 我們考慮從S一路沿鏈往上跳,發現跳到1號點的時候就已經超過T了, 所以最多能跳到3號點, 也就是最多能搜集到P2
很簡單, 鏈的情況我們已經解決了
然而這個演算法的複雜度是O(n)的, 我們考慮優化。這時候,如果對lca十分熟悉的話, 就會想到在樸素lca中, 深度較大的那個節點會一直往上跳, 直到與另一個節點深度相同,與這個情況十分相同。
最後,lca採用倍增優化的方式往上跳
for(int i=20;i>=0;i--)if(deep[f[x][i]]>=deep[y])x=f[x][i];
從大到小枚舉, 如果深度沒有超過另一個節點就往上跳
自然而然的想到,這道題也可以用倍增來跳, 預處理一個f數組, Fi, j 表示i號點, 下2^j個需要搜集的寶石的位置, 只要沒有超過T就直接往上跳
for(int i=25; i>=0; i--){ int next = f1[now][i]; if(t!=0 && deep[next]>=deep[T]) now=next, i=25; }
好!鏈的情況解決鏈, 一般情況就很簡單了。

(是不是講的有點太細了
不難發現, S-T的路徑被lca分成兩部分。
對於S的那一部分,可以採用鏈的方法解決, 這時候我們得到一個Px:S鏈最遠能匹配到的寶石,在上圖中, x=2
對於T鏈, 我們並不能從lca往下跳(顯然), 我們考慮從下往上跳。
我們讓p4指向p3(剛好相反), 也就是讓每個點指向上一個要搜集的寶石。
不妨從一個Py點開始向上跳, 假如能跳到一個Px+1, 那麼Py就可以被搜集到(因為S已經從P1搜集到x了, T又從x+1搜集到y了,所以可以從1搜集到y)。
那麼答案是不是可以搜集到y個呢?顯然不是, 萬一某個Pz也能夠跳到Px+1, 而z>y呢
這時候仔細思考,答案有單調性,可以二分,(因為假如能從1搜集到z,肯定也能從1到y…)
所以最終的思路: 二分可以搜集到第幾個顏色, 如果可以從該節點跳到x+1(倍增), 則滿足
複雜度
簡單實現
實現很簡單
1. 首先預處理三個倍增, 第一個普通倍增求LCA, 另外兩個是S, T鏈上的倍增。
既然要倍增, 我們首先要知道每個節點的父節點,然後dp。對於這道題, 我們要知道對於某個點Px, 祖先中離他最近的Px+1, Px-1才行。怎麼做呢?
很簡單:對樹進行dfs,開一個棧stack s[N]; 每到一個點Px就把節點編號壓入s[x], 回溯的時候彈出就好了。所以 (S鏈)f1[x][0]=s[x+1].top(), (T) f2[x][0]=s[x-1].top();然後普通倍增就好了
for(int i=1; i<=n; i++){ for(int j=1; j<=28; j++){ f[i][j] = f[f[i][j-1]][j-1]; f1[i][j] = f1[f1[i][j-1]][j-1]; f2[i][j] = f2[f2[i][j-1]][j-1]; } }
2.從S點找到最近的P1(s不一定是P1), 然後往上跳, 求Px。這一步可以在上一步記錄每一個節點最近的P1;
3.在T鏈二分能匹配第幾個寶石, 對於每個Py, check的時候找到離T最近的Py往上跳(唉等等,這怎麼找?總不能開個NM的數組在第一步記錄吧?事實上可以離線來做, 再掉用一遍dfs, 搜索到某x點時,棧中就是每種顏色離x最近的 ,這個時候求出所有T為x的詢問)
至於程式碼, 實現已經講了就不放吧,沒多長
其實是我tcl不想整理


