Codeforces Global Round 14 E. Phoenix and Computers
- 2021 年 5 月 3 日
- 筆記
- Codeforces, DP, dp專題, 思維
題目鏈接
題目大意
給定 \(N\) 台電腦,起初每台電腦都是關閉的
現在你可以隨意打開電腦,但如果第 \(i-1\)、第 \(i+1\) 台電腦是開啟的,則第 \(i\) 台電腦也會自動開啟,而你無法手動開啟它
問你有多少種打開電腦的方法,使得最後所有電腦都是開著的
解題思路
分成兩步來解決.
第一步:
考慮:如果 \(N\) 台電腦我都要手動開啟,有多少種方法?
可以枚舉是從哪台電腦開始打開:
- 從 \(1\) 開始,剩下的 \(N-1\) 必須按照 \(2,3,…,n\) 的順序開(不理解可以畫一下)
- 從 \(2\) 開始,對於 \(2\) 左邊的電腦 \([3\)~\(N]\),\(4\) 必須在 \(3\) 開了之後開,\(5\) 必須在 \(4\) 開了之後開 \(…\) ,而 \(1\) 可以在任意時刻開機
- \(…\)
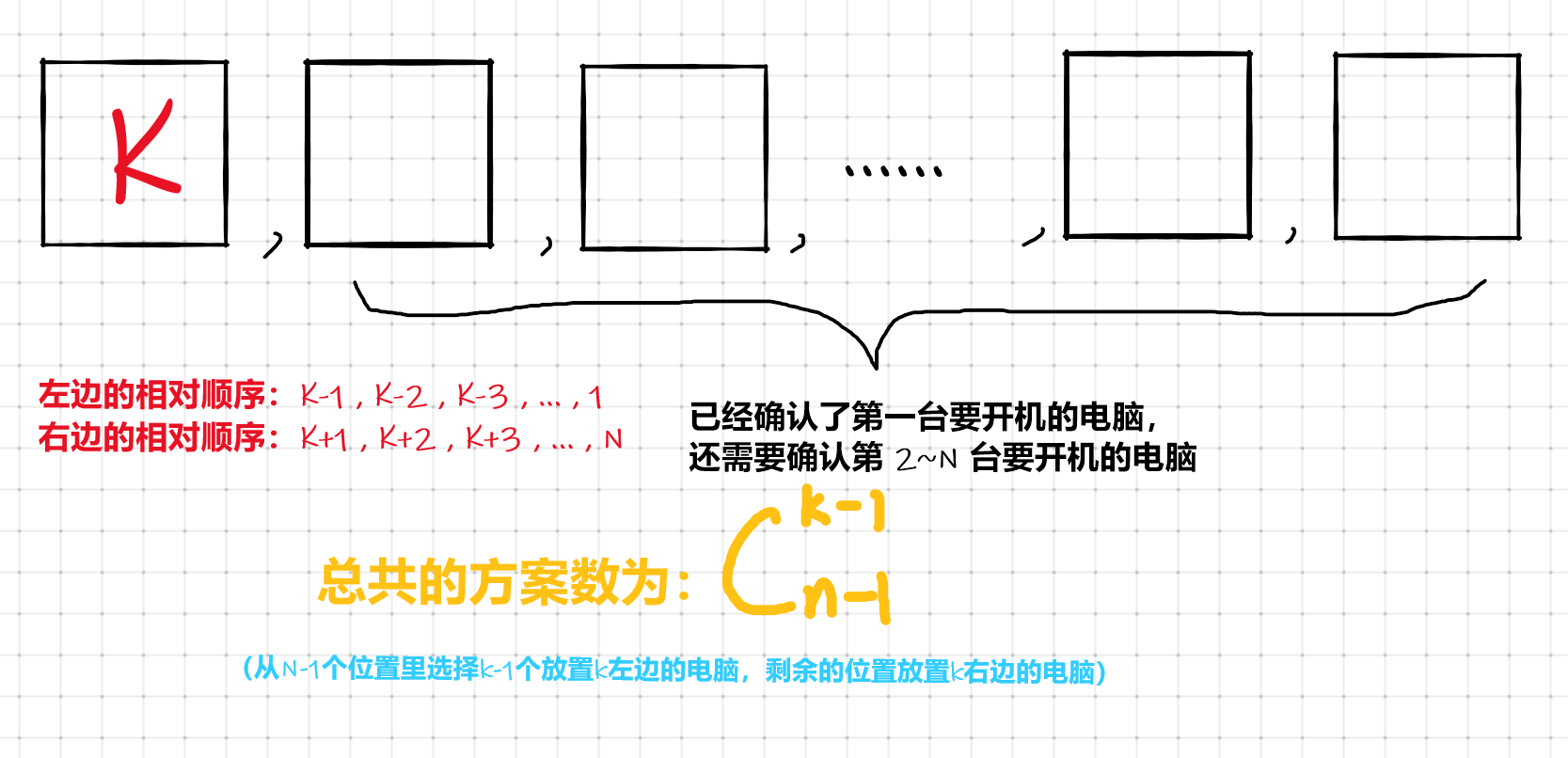
- 從 \(k\) 開始開,對於 \(k\) 左邊的電腦, 它們的相對開機順序必須是 \(k + 1 , k + 2 , … , n\)
對於\(k\) 右邊的電腦,它們的相對開機順序必須是 \(k-1,k-2,…,1\)
不過左右兩邊的開機順序是可以穿插(合併)在一起的
所以手動開啟 \(N\) 台電腦的方案數為 \(C_{n-1}^{1}+C_{n-1}^{2}+\ldots +C_{n-1}^{n-1} = 2^{n-1}\)
第二步:
考慮:最後電腦開啟的狀態?
顯然最後電腦開啟的狀態會是這樣的:
手動開啟 \(1\sim X_1\) → 自動開啟 \(X_1+1\) → 手動開啟 \(X_1+2\sim X2\) 台 →自動開啟 \(X_2+1\) → \(…\) → 手動開啟 \(X_{n-1} + 1\sim X_n\) ,其中需要保證 \(X_i + 1 < N\)
於是我們可以定義 \(f[i][j]\) 表示:前 \(i\) 台電腦,手動打開了 \(j\) 台, 第 \(i\) 台是手動打開的 , 第 \(i + 1\) 台是自動打開的方案數。
那麼 \(f[i][j]\) → \(f[i + 1 + K][j + X_i]\) 的意義為:
手動打開 \(pos \sim i\) → 自動打開\(i+1\) → 手動打開 \(i + 2 \sim X_i\) 的過程。
- \(f[i+1+X_i][j+X_i]\) 相對 \(f[i][j]\) 又多手動開啟了 \(X_i\) 台電腦
- 這 \(X_i\) 台的電腦的開啟方案數有 \(2^{Xi-1}\)種(第一步得出的結論)
- 然後考慮將這 \(X_i\) 台”新”電腦開機的順序和 \(j\) 台”舊”電腦開機的順序穿插(合併)在一起。
即現在有 \(X_i+j\) 個開機順序需要確認,我們可以從中選 \(X_i\) 個放”新”電腦的開機順序,剩下的放”舊”電腦的開機順序,那麼方案數為 \(C_{X_i+j}^{X_i}\) (或者 \(C_{X_i+j}^{j}\)也可以)所以可得: \(f[i + 1 + X_i][j + X_i] = f[i][j] \times 2^{Xi-1} \times C[j + X_i][X_i]\)
答案即: $ans=\sum ^{n}_{i=0}f\left[ n\right] \left[ i\right] $
\(i\)、\(j\)、\(X_i\) 都可以通過枚舉得到
寫題解不易,如有幫助到您請點個贊給予我一點小小的鼓勵!
AC_Code
#include<bits/stdc++.h>
using namespace std;
const int N = 4e2 + 10;
long long C[N][N] , bit[N];
long long n , m , ans , f[N][N];
void init(int mod)
{
bit[0] = 1;
for(int i = 1 ; i <= N - 10 ; i ++) bit[i] = bit[i - 1] * 2 % mod;
for(int i = 0 ; i <= N - 10 ; i ++)
{
C[i][0] = 1;
for(int j = 1 ; j <= i ; j ++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
}
}
signed main()
{
cin >> n >> m;
init(m);
for(int i = 1 ; i <= n ; i ++)
{
f[i][i] = bit[i - 1];
for(int j = 0 ; j <= i ; j ++)
{
for(int k = 1 ; k + i + 1 <= n; k ++)
{
f[i + 1 + k][j + k] += f[i][j] * bit[k - 1] % m * C[j + k][k] % m;
f[i + 1 + k][j + k] %= m;
}
}
}
for(int i = 0 ; i <= n ; i ++) ans += f[n][i] , ans %= m;
cout << ans << '\n';
return 0;
}