一維繩波模擬中的探究:完全吸波性邊界條件
完全吸波邊界條件:
波動方程模擬在計算物理中佔有重要的地位,具體應用有聲學振動模擬、電磁波模擬、波函數模擬等。這些波動方程(除波函數外)都具有一個大致相同的形式:
\]
其中\(u\)為某標量場,\(c\)為聲速。
這類方程必定有行波解,在一維情況下,解可以表示為:
\]
即解可以表示為兩列相反傳播的行波\(u_1\)、\(u_2\)的疊加。其中\(u_1\)、\(u_2\)為任意一元函數。
這種方程的求解除了與初始條件相關,還與邊界有很大關係。邊界處一般設置為固定或自由邊界條件,兩種邊界在性質上有些許區別,但又有相似性,例如都能實現完全反射,從而形成駐波。
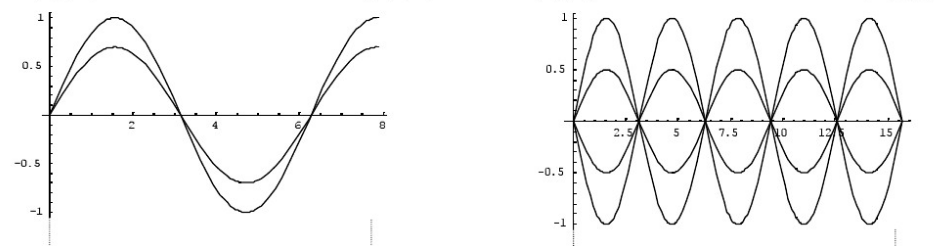
上面兩張圖為一維繩波的模擬(幾個時刻的圖形疊在一起)。每張圖左端有一個波源,在做正弦振動,而左段為不同的邊界條件,導致不同表現。左圖為自由式邊界條件,繩頭可以自由擺動。右圖為固定式邊界條件,繩頭強制固定在0處。
由於波源發出的能量無法被繩頭耗散,兩種情形下波都會被繩頭反射,從而產生駐波。
於是,自然可以想像,會不會有一種邊界條件,使右行波完全被吸收,從而不產生任何反射呢?答案是有的。可以想像,假如繩子繩頭之外還有繩較長的延伸,從而做到在實驗關心的時間之內,右行的波還沒有碰到真正的邊界,不存在反射,則右行的波就好像被「完全吸收」了。就是說,無限長繩等價於完全吸波條件。
但是電腦永遠模擬不了無限,而只能用有限長的繩子近似「完全吸波條件」。因而實驗時間不能太長,至少在反射波進入人們關心的區域之前,必須中止模擬,否則「完全吸波條件」失效,模擬會出現很大偏差。
並且即使這樣,還是浪費了大量的計算資源在人們不關心的區域的波動方程計算上。這註定是一個糟糕的方法。
存不存在更好的方法?其實是有的。仔細觀察模擬的機制,只要對繩頭進行人為的操縱,讓繩頭的行為表現得和無限長繩情況下一模一樣,就可以「騙過」左方的繩子,讓繩子「以為」右行波還沒有碰到邊界,從而不會發生反射。
但是該如何認為移動繩頭才能讓繩頭「矇混過關」呢?天真的想法是利用該問題中只包含右行波的特點:
\]
在該解中,繩子上每一個點的運動狀態都滯後重複前面的點的運動狀態,即:
\]
那麼繩頭只需要簡單地滯後重複某個相鄰點的運動,即可完美地實現「完全吸波」。
然而數值模擬殘酷地表明,這種方法完全行不通!具體原因和數值離散過程密切相關,筆者能力和精力有限,並沒有進一步研究。
幸好,繩波系統有一個十分優異的特性——線性,將繩頭視為一個系統,繩頭的位移看成系統的輸出端,而與繩頭相連的倒數第二個節點的位移看成該系統的輸入端,則該系統是一個線性時不變系統。該系統的含時響應完全線性取決與輸入端的位移方程。
數學推導:
取繩頭的位移為\(u_o(t)\)(輸出),而繩頭前一個節點的位移為\(u_i(t)\)(輸入),則線性時不變系統有如下優良特性:
\]
又由於:
u_o(t)&=\int_0^t{u_i(t-p)dF(p)}\\
&=-\int_0^t{F(p)du_i(t-p)}+[u_i(t-p)F(p)]\bigg|^t_0
\end{aligned}
\]
式中,\(F(t)=\int^t_0f(t)dt\),因而最後一項為0。上式最終化簡為:
\]
我們把\(F(t)\)叫做繩頭的「衝擊響應函數」,因為如果輸入函數具有以下形式:
\begin{aligned}
0,t\lt\epsilon\\
1,t\ge\epsilon\\
\end{aligned}
\]
其中\(\epsilon\)為一無限接近0的小量,則輸出函數為:
u_o(t)&=\int_0^t{F(p)\dot{u_i}(t-p-\epsilon)dp}\\
&=\int_0^t{F(p)\delta(t-p-\epsilon)dp}\\
&=F(t-\epsilon)\\
&=F(t)
\end{aligned}
\]
衝擊響應函數反映了當輸入函數為階躍函數時,輸出端的變化情況。我們接下來的工作就是找到這個階躍函數。
在數值模擬中,繩波系統可以離散為有多個節點的一條長鏈,相鄰節點之間用彈簧連接,彈簧施加線性恢復力。對於第\(n\)個節點的位移\(u_n(t)\),運動學方程如下:
\]
可以通過設置\(t’=t\)實現無量綱化:
\]
繩波模型的離散化示意圖:

由於該系統實際上具有無限多個節點力學分析將變得十分棘手。但是,有一種方法可以巧妙破解這一難題,從而實現物理系統的方程化:
考慮倒數第1、2個節點,設它們對左方的衝擊響應函數分別為\(F_A(t)\)和\(F_B(t)\),由於系統右端為無限長序列,則應該有:
\]
現在考慮運動方程:
\ddot{u_A}(t)&=\frac{1}{2}(1-2u_A(t)+u_B(t))\\
u_A(t)&=F(t)\\
u_B(t)&=\int_0^t{F(p)\dot{u_A}(p-t)dp}
\end{aligned}
\]
聯立方程有:
\]
其中初值條件為:
F(t)&=0\\
\dot{F}(t)&=0
\end{aligned}
\]
這個方程是一個積分微分混合型方程,並且由於涉及到卷積,難以有效消除積分號,筆者能力有限難以給出解析解。不過該方程可以用皮卡迭代序列給出級數解。經過艱苦卓絕的求解(玄學找規律),筆者得到級數式為:
\]
利用Python繪圖顯示影像:

可見當時間趨於無窮時,系統會逐漸穩定在1附近,這符合繩波衝擊響應函數的特點。
註:由於泰勒級數收斂性較差,該級數用double精度計算會在\(x=20\)之後發散。為了正確計算,必須提高計算精度。高精度計算的方法在博文Java 高精度浮點數計算工具中有所介紹。
只要繩頭的位移始終滿足:
\]
即能做到完全吸收向右傳來的波,而避免反射波產生,即「完全吸波邊界條件」。
但是,上式還有一個問題,即仍然需要無限大的儲空間才能記錄所有時刻的\(u_i(t)\),方法仍然沒有可行性。為了解決這一問題,注意到:
\]
可以設置截斷距離\(L\),使積分近似為:
u_o(t)&=\int_0^L{F(p)\dot{u_i}(t-p)dp}+\int_L^t{F(p)\dot{u_i}(t-p)dp}\\
&\approx\int_0^L{F(p)\dot{u_i}(t-p)dp}+\int_L^t{1*\dot{u_i}(t-p)dp}\\
&=\int_0^L{F(p)\dot{u_i}(t-p)dp}+u_i(t-L)
\end{aligned}
\]
至此,數學推導部分已經全部完成,只剩下程式實現了。
程式模擬:
由於筆者使用java做科學計算的習慣(怪癖),程式由java實現。共編寫兩個類,一個類進行繩波模擬,另一個專註於計算繩頭的衝擊響應。以下是模擬結果。
固定式邊界條件:

自由式邊界條件:

完全吸波邊界條件:

可以看出,完全吸收式邊界條件較為出色地完成了任務,波包到達邊界後幾乎沒有反彈,就好像邊界為無窮大一樣。
程式碼:
見我的github頁面,測試程式碼也在裡面。程式程式碼比較容易理解。
結束語:
通過本文的推導,我們得出了完全吸波邊界的一種可行方法,該方法在電腦波動模擬中十分有用,尤其適用於包含無窮大場景,需要排除反射波的情況。不過筆者沒有想出來如何在2維以上波動系統中實現類似邊界條件。
* 本文為筆者課程學習閑暇時的一點思考,可能有naive的地方。公式推導基本是自己腦洞的,專業性欠缺,如果有誤請各位高人指正。

