AI數學基礎之:確定圖靈機和非確定圖靈機
簡介
圖靈機是由艾倫·麥席森·圖靈在1936年描述的一種抽象機器,它是人們使用紙筆進行數學運算的過程的抽象,它肯定了電腦實現的可能性,並給出了電腦應有的主要架構,引入了讀寫與演算法與程式語言的概念為現代電腦的發明打下了基礎。
本文將會講解一下圖靈機中的兩種類型:確定圖靈機和非確定圖靈機。
圖靈機
圖靈機是一種數學計算模型,它定義了一個抽象機器,該抽象機器根據規則表來操縱帶子上的符號。儘管該模型很簡單,但是在任何給定電腦演算法的情況下,都可以構建出模擬該演算法邏輯的圖靈機。
簡單點說,圖靈機就是一個模擬演算法運行的抽象機器。它是這樣定義的:
- 有一個無限長度的磁帶,這個磁帶被分成了一個接一個的單元格,磁帶被用於寫入字母和符號。
- 一個讀寫磁帶的磁頭,這個磁頭負責控制堆磁帶的寫入和左右移動。
- 一個狀態暫存器,用來存儲圖靈機的狀態。
- 一個指令表,可以根據機器當前所處的狀態和磁帶上當前的符號,指示機器進行特定的操作。比如:擦除或者寫入一個符號、向左或者向右移動磁頭。
可以看到整個圖靈機基本上模擬了程式的執行步驟。
圖靈機雖然可以表示任意的計算程式,但是因為其極其簡單的設計實際上並不適合進行計算,所以現實世界的現代電腦都是對圖靈機的優化設計。
圖靈完備性是指指令系統模擬圖靈機的能力。從理論上講,圖靈完整的一種程式語言可以表達電腦可以完成的所有任務。如果忽略有限記憶體的限制,幾乎所有程式語言都是圖靈完備的。
圖靈機的缺點
雖然圖靈機可以表示任何計算任務,但是圖靈機太過於簡單了,在某些複雜的模型中無法很好的進行使用。比如在現代電腦中的RASP隨機存儲模型,因為RASP可以在暫存器中引用其他的暫存器,所以可以基於記憶體索引進行優化,這種優化是在圖靈機中無法實現的。
圖靈機的另一個限制是它們不能很好地進行並發建模。另外,因為在早期的時候,電腦的使用通常僅限於批處理,即非互動式任務,每個任務都從給定的輸入數據中產生輸出數據。 所以圖靈機在描述現代互動式應用也有一些限制。
等效圖靈機
因為圖靈機是一種假想的設備,它為電腦演算法的概念提供了理論基礎。並且因為圖靈機模型比較簡單,對於複雜問題的描述比較弱,所以出現了很多圖靈機的等效模型,雖然這些模型並不一定比圖靈機強大,但是這些模型是真正存在的,並且使用他們可以更加容易的解決特定問題。
確定圖靈機
在確定性圖靈機(DTM)中,其控制規則規定了在任何給定情況下最多只能執行一個動作。
確定性圖靈機具有轉換功能,對於磁帶頭下的給定狀態和符號,該轉換功能指定了三件事:
要寫入磁帶的符號,頭部應移動的方向(向左,向右或都不向),以及有限控制的後續狀態。
例如,狀態3的磁帶上的X可能會使DTM在磁帶上寫Y,將磁頭向右移動一個位置,然後切換到狀態5。
非確定圖靈機
在理論電腦科學中,非確定性圖靈機(NTM)是一種理論計算模型,其控制規則在某些給定情況下指定了多個可能的動作。 也就是說,NTM的下一個狀態不是完全由其動作和它所看到的當前符號決定的(不同於確定性圖靈機)。
例如,狀態3的磁帶上的X可能允許NTM:
輸入Y,向右移動,然後切換到狀態5或者寫一個X,向左移動,並停留在狀態3。
那麼問題來了,對於非確定圖靈機來說是怎麼進行下一步的選擇的呢?實際上NTM足夠幸運,它總是會選擇那個能夠最終指向接受狀態的那一步。
你可以把NTM的諸多分支看成是許多副本,每個副本遵循一個可能的轉換。 DTM遵循的是單個「計算路徑」,而NTM則是「計算樹」。 如果樹中至少有一個分支導致接受狀態,那麼NTM就會接受這個輸入狀態。
我們看下兩者的決策圖:
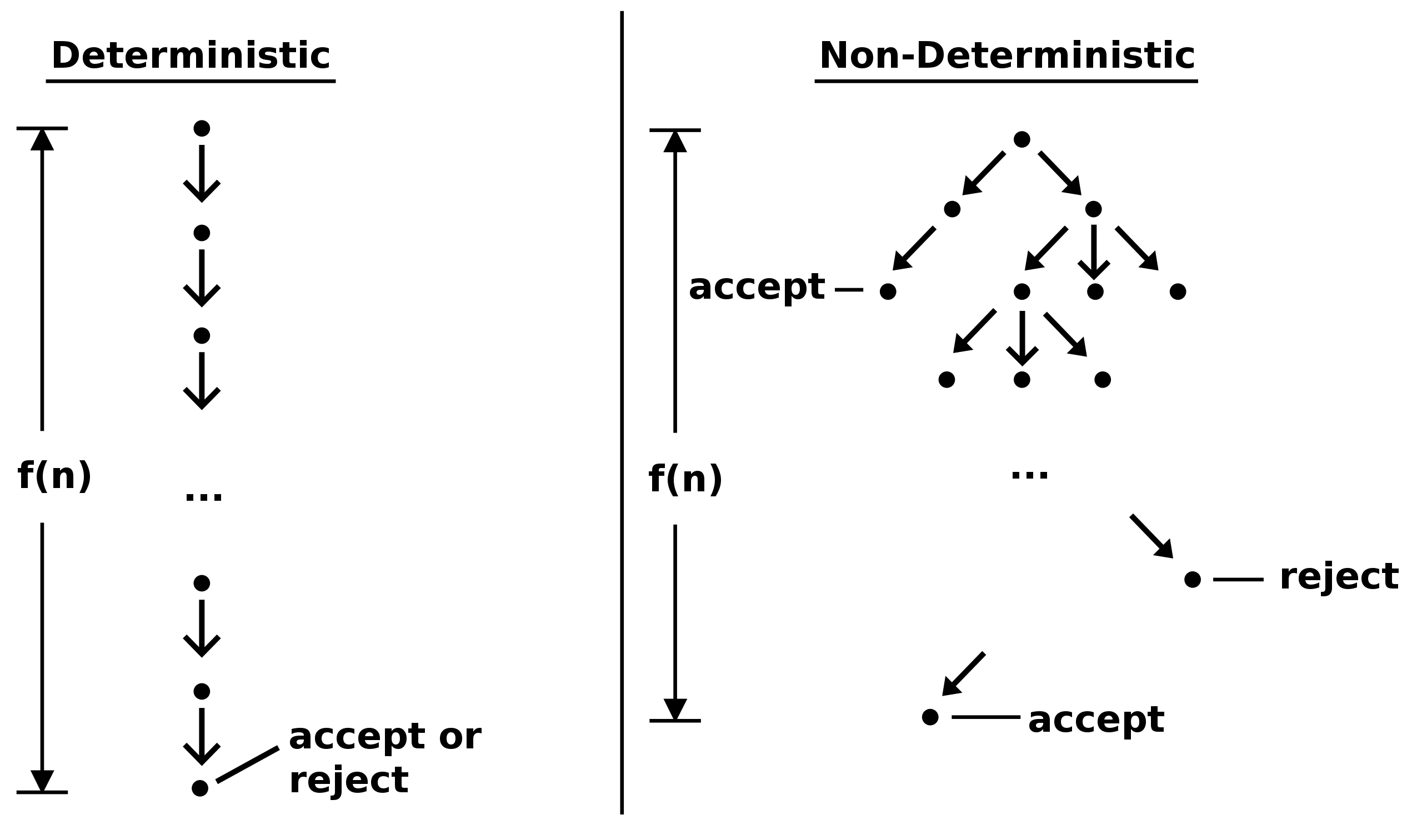
確定圖靈機和非確定圖靈機 兩者在計算上是等效的,也就是說,儘管它們通常具有不同的運行時,但可以將任何NDTM轉換為DTM(反之亦然)。 這可以通過構造來證明。
本文已收錄於 //www.flydean.com/03-turing-machine/
最通俗的解讀,最深刻的乾貨,最簡潔的教程,眾多你不知道的小技巧等你來發現!
歡迎關注我的公眾號:「程式那些事」,懂技術,更懂你!


