002-深度學習數學基礎(神經網路、梯度下降、損失函數)
002-深度學習數學基礎(神經網路、梯度下降、損失函數)
這裡在進入人工智慧的講解之前,你必須知道幾個名詞,其實也就是要簡單了解一下人工智慧的數學基礎,不然就真的沒辦法往下講了。
本節目錄如下:
- 前言。
- 監督學習與無監督學習。
- 神經網路。
- 損失函數。
- 梯度下降。
0. 前言
人工智慧可以歸結於一句話:針對特定的任務,找出合適的數學表達式,然後一直優化表達式,直到這個表達式可以用來預測未來。
接下來就來一句一句的分析這句話:
- 針對特定的任務:
首先我們需要知道的是,人工智慧其實就是為了讓電腦看起來像人一樣智慧,為什麼這麼說呢?舉一個人工智慧的例子:
我們人看到一個動物的圖片,就可以立刻知道這個動物是貓,還是狗。但是電腦卻不可以,如果電腦可以分出類別,那麼這就會是一個具有影像分類功能的人工智慧小例子。
這裡的影像分類就是我們所說的特定任務,這就是我們希望寫出一個人工智慧的程式來做的事情。
還有一些其他的常見的任務:人臉識別,目標檢測,影像分割,自然語言處理 等等。
- 找出合適的數學表達式:
學過高等數學並且有電腦思維的人都知道,世界中幾乎所有的事情都可以用數學函數來表達出來,我們先不管這個數學表達式是離散還是連續,也不管他的次數多高,反正他能達到表示特定任務的一種目的。
比如說,針對一個西瓜品質好壞的預測任務,可以設出以下的表達式:

解釋如下:
1、
x1,x2,x3可以看作判斷西瓜好壞的判斷依據,比如可以是:瓜皮紋路,敲擊聲音,瓜皮顏色等等。2、
a,b,c,d就是這個表達式的係數,一旦數學表達式定下來了,那麼接下來需要做的事情就是找出合適的係數,使得這個表達式可以很好的判斷出西瓜品質的好壞。
所以,針對上文提到的特定任務,都可以用數學表達式表示出來,當然,我們會儘可能找簡單、高效的表達式。
- 一直優化這個表達式:
上邊引出表達式之後,會發現當表達式確定下來之後,就要尋找合適的係數了,尋找係數的過程就被稱之為訓練網路的過程。
我們優化表達式的重要思想是:一直調整係數值,使得預測出的數據 與 真實數據之間的差距儘可能的最小。
比如:假設預測的數據是 f1(x),真實數據是y,我們通過一直改變係數的值,來找出可以使得預測數據與真實數據之間距離最小的一組,最小的一組數據就是我們需要的係數。
其中,距離計算公式可以是如下的表達式:

通過這個表達式,得到的 loss 值就是真實值與預測值之間的距離。
然後,接下來的優化就是針對這個loss 表達式來進行的,目的就是讓loss的值達到最小。
因為loss值達到最小的時候,就意味著我們的預測值與真實值距離很相近,預測越準確。
這裡值得一提的是,這裡的
loss表達式的優化過程,其實就是將loss公式對函數f(x)的係數求導。所以當
loss最小的時候,就意味著此時的係數最合適。具體的細節往下看。
- 用優化好的表達式預測未來:
經過上邊的優化,此時函數會得到一個相對好一點的係數,然後就可以使用這個函數來預測未來的事情了。
這就是達到了人工只能的目的了。
所以,下邊我們就要仔細討論,數學表達式的構建,距離函數的構建,距離的優化。
1. 神經網路
神經網路的英文是:neural network (簡稱:NN)。
神經網路其實就是變形的數學表達式,它通過拼裝基礎組件(神經元)來模擬出數學表達式。
1.01. 什麼是神經網路
一說神經網路,大家首先想到的就是神經元,其實沒錯,神經網路這個名詞就是從神經元這裡演變過來的。所以我們做一下類比。
1.01.001. 神經元

如圖所示,這個圖就是我們人體的神經元的放大圖。
通常我們身體的 A 部位發出的命令,要指揮 B 部位響應,就要通過 A 向 B 發出訊號。這個訊號的強弱影響著 B 反應的強弱。
所以,這就是神經網路的構思所在:
構建出一個類似於神經元的結構,上一個節點的輸入(A處的控制) 以及權重(訊號的強弱)共同決定下一個節點的輸出(B處的反應)。
這句話,現在看不懂沒關係,有個印象就好,繼續往下看吧。
1.01.002. 神經網路

如圖所示就是一個最簡單的神經網路結構,這個結構的數學表達式是:
圖中的圓圈我們就把他類比於神經元,圖中的各個結構解釋如下:
-
其中
X1,X2就是這個神經網路的輸入,他相當於就是人體大腦發出的控制命令。 -
W1,W2就是權重,他是用來控制不同輸入訊號佔比大小的數據,比如:想讓控制X1作用明顯一點,那麼對應的W1就大一點。 -
Y就是輸出,他就是輸入數據與權重作用之後的最終結果,在神經元中也就是最終對身體某個部位的控制訊號。
1.02. 神經網路的數學原理
神經網路的數學原理非常簡單,簡單總結下來就是一句話:不同的輸入作用於各自的權重之後的和即為我們需要的結果。
其實就可以大致理解為我們的函數 :
f(x) = a*x1 + b*x2一樣,所謂的權重就是我們方程的係數。
細心的人觀察上邊的公式就會發現,一個神經元節點就可以歸結於一個運算式子。所以我們這裡就來針對上圖,分析分析含有一個神經元節點的公式。

從圖中可以看得出來,最終的輸出結果 Y 是由 輸入(X) 以及 權重(W) 共同決定的。
他們最終的計算結果 Y 其實說白了就是一個計算公式:Y = X1*W1 + X2*W2 ,這個公式的含義大家應該都明白,給不同的輸入 分配不同的權重 ,從而得到想要的結果。
這就是神經網路中一個神經元的數學原理,當把神經元的個數增多之後,原理以此類推,只不過是要增加權重W以及輸入X的個數而已。
下邊就可以看作是一個,含有兩層的神經網路結構。

-
第一層節點:
11,12,13。第二層節點:21。 -
輸入:
X1,X2。 輸出 :Y。
於是,根據公式:輸出 等於 輸入作用於 權重, 得出以下推導 :
- 輸入:
X1,X2。 - 節點
11的值: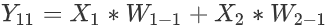 .
. - 節點
12的值: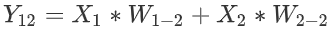 .
. - 節點
13的值: .
. - 節點
21的值就是最終輸出Y: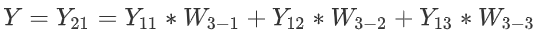 .
.
所以,最終的整合式子為:

於是,我們可以發現,類似於這樣的堆疊方式,我們可以組合成很多的數學函數。
這就是神經網路,他的目的在於將數學公式堆砌出來,至於為什麼要這樣堆砌,是因為這樣堆砌電腦計算比較方便唄。
1.03 總結
到目前為止你已經知道了神經網路的由來,並且知道神經網路與數學公式之間的關係。
此時你需要明確的知識點是:
- 人工智慧就是使用已有的數據,擬合出一個可以用來預測未來的公式。
- 這個公式的係數需要一直調整,從而找出一組最為合適,正確率較高的係數。
- 因為係數的尋找需要大量的計算,所以需要將這個公式用神經網路表示出來的,因為在電腦中這樣表示的時候計算最為方便。
2. 監督學習與無監督學習
這個知識點比較簡單,就一些單純的概念。
監督學習:就是我們收集到的數據是有標籤的。
就是說,我們收集到的數據是已經分好類的。
比如說:當前當前有一批樣本數據,
x1, x2, x6, x9, x13屬於類別y1類。x3, x4, x5, x8, x11屬於類別y2類。x7, x10, x12屬於類別y3類。
然後接下來我們使用這些數據的時候,就可以使用已有標籤的數據,去擬合出曲線,用以預測未來。
無監督學習:我們收集到的數據是無標籤的。
就是說,收集到的數據並沒有固定的類別,我們需要做的事情就是挖掘數據內部的聯繫,給他們聚類,找出類別。

如圖所示,挖掘出數據內部的聯繫,讓他自動歸類。
3. 損失函數
上邊解釋過了,損失函數的作用就是計算 真實值 與 預測值 之間距離的 (距離其實可以簡單理解為兩個數據之間的差距)。
這裡介紹一些常見的幾種損失函數,以供大家入門使用。
3.01. 一些前提
這裡給定一些大前提,下邊的幾種損失函數通用的那種。
- 真實值:
y,他就是針對某一組輸入x的真實標籤。 - 預測值:
f(x),他就是針對輸入x的預測標籤。 - 樣本數:
m,他就是我們每次輸入多少樣本進行計算,比如:某一次輸入5組x,得到5個預測結果,這裡的m=5.
3.02. 絕對值損失函數
其實就是簡單的計算 真實值 與 預測值 之間的絕對值距離而已。
公式:

解釋:
J(y,f(x))的意思就是,這個損失函數的參數是:真是標籤y與 預測數據f(x)。J(w,b)的意思是,這個損失函數的目的是優化參數w與b。這裡的w,b其實就是係數的矩陣形式。- 後邊具體的計算公式就是:輸入有
m個樣本,計算出這m個樣本的距離絕對值和,然後再求均值。
3.03 均方差損失函數
就是將上邊式子的絕對值換成平方就好了。
公式:

解釋:
- 這裡只是將絕對值換成了平方,除以
m換成了除以2m。
3.04 交叉熵損失函數
這個就比較麻煩了,交叉熵損失函數一般用於解決分類問題。
標籤:
在通常的分類問題中,標籤y的取值一般只有 0 或 1 。
1 表示是當前類別, 0 表示不是當前類別。
公式:

解釋:
- 上邊說了,
y與f(x)都只能取1與0中的一種可能性。所以,上述公式的效果就是: - 如果 y與 f(x) 相同,則 J = 0.
你帶入
y=1 , f(x)=1試試就知道了。
- 如果 y與 f(x) 不同,則 J = 無窮大.
你帶入
y=1 , f(x)=0試試就知道了。
3.05 總結
到這裡你已經學習了三種常見的損失函數。
此時你應該有一個明確的知識點就是:
- 損失函數是用來計算真實值與預測值之間距離的。
- 當損失函數的值越小就代表著真實值與預測值之間的距離就越小,也就意味著預測的越准。
4. 梯度下降
好了好了,上邊過完理論知識,這裡來一個真真正正的數學內容了,其實不難,看我慢慢分析。
- 上邊我們提到對數學函數優化的時候,只是介紹了理論的知識。
我們知道了損失函數就是衡量預測值與真實值之間距離的公式。
並且知道,損失函數的值越小,真實值和預測值之間的距離越小,也即:預測的越准。
- 但是並沒有帶著大家深入探究如何優化。
也就是沒有告訴大家怎麼使得損失函數的值越來越小。
其實,這裡使用的數學知識就是 :求偏導
4.01. 數學例子
這裡以一個簡單的數學例子來引入梯度下降的內容。
- 場景引入
在數學課中我們經常做的一個題型就是:已知一個函數
f(x)的表達式,如何求出這個式子的最小值點。
在數學題中我們經常用的方法就是:將函數f(x)對x求導,然後令導數式子為0,求出此時的x的值,即為最小值點的位置。
- 具體例子
求函數
的最小值點,並且求出最小值。
對函數求導

令導函數為0,求出此時的x

此時,x = 3 即為函數 f(x) 的最小值點,帶入原方程 f(3)= 2*9-12*3+20 = 2.
這個解題過程,想必大家都很熟悉吧。
下邊就分析一下這個過程的數學原理了
4.02. 數學例子原理
梯度就是導數。
針對上邊提到的方程的最小值求解,其實就是求出其梯度(導數)為0的位置,就是其最低點的位置。具體看下圖:
- 方程
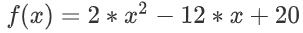 影像如下:
影像如下:

從圖中可以看出,方程在不同位置的導數方向是不同的,只有在最低點的位置,導數為
0,所以可以用導數為0的位置求出最低點。
上邊舉的例子是一個比較簡單的例子,方程中只有一個未知數,但是在真實情況中,往往一個方程有很多未知數。
- 比如:
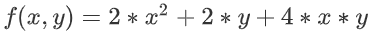
此時需要做的事情就是針對每一個變數求偏導,求出該方程針對每個變數的梯度方向 (梯度方向就是數據變小的方向)。
於是,在方程的每個點上,都有多個梯度方向,最終將這多個方向合併,形成這個點的最終梯度方向 (數據變小的方向)

如圖,方程有兩個變數
x,y,於是在A點針對兩個變數求偏導就可以得到各自的梯度方向(兩個紅色箭頭的方向)。然後,將兩個梯度進行合併,得到最終的梯度方向
Z。Z方向就是方程在A點數據變小的方向了。
4.03. 完整例子
上邊講完原理,這裡就舉出一個例子,帶著大家走一遍梯度下降找最小值的過程。
假設此時的方程已知,並且根據方程繪製出的影像如下。

- 剛開始我們位於A點:
1、在A點處針對方程的各個變數求出偏導,於是便可以得到方程針對各個方向的梯度方向。
2、將A點處各個方向的梯度方向進行合併,形成最終的梯度方向。
3、最終的梯度方向就是AB方向。
4、於是向著AB方向走出一段距離,走到了B點。
- 到達B點: (思路同上)
1、求出B點處各個方向的梯度方向,然後合併所有梯度方向,得到最終的B點處梯度方向 BC。
2、於是沿著BC方向,走出一段距離,到達C點。
- …重複上述過程:
到達某個點之後,求出各方向的偏導數,然後合併得到最終的梯度方向。
然後沿著合併後的梯度方向走出一段距離到達下一個點。
然後在一直重複……
- 到達K點:
K點就是最終的點,這就是優化得到的最重點。
這就是整個找最小點的可視化過程,但是其中提到更新的數學細節並沒有提到,所以下邊提一下用到的數學更新公式吧
4.04. 更新公式
一般我們梯度下降更新的數據只有函數的係數,然後函數的係數可以分為兩類:權重(W)+ 偏差(b)
所以,更新的時候也就針對這兩個參數就好了。
變數定義:
W: 方程的權重。 (可以簡單理解為方程變數前面的係數)b:方程的偏差。 (可以簡單理解為方程中的常數)
比如:
中,
2 , 1就是權重,3就是偏差。
公式:
- 更新權重
W: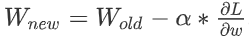 .
.
原始點的權重是
,原始點此時針對
W的梯度方向是.
α就是一段距離長度(它就是我們上文一直提到的走一段距離)。所以
表達的含義就是沿著
W的梯度走一段長度為α的距離。然後 新的
W就是 舊的W減去那一段方向長度。
- 更新偏差:
 .
.
原理同
W.
這就是更新參數的整個梯度下降過程了。
5. 總結
到目前為止,基礎的人工智慧知識已經基本講完了,這個時候我們再來仔細品味這句話。
針對特定的任務,找出合適的數學表達式,然後一直優化表達式,直到這個表達式可以用來預測未來。
或許你就會有不一樣的體會了。
ok,下一節就講一講Pytorch的基礎使用,然後就是最終的手寫體數字識別任務了。
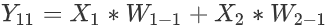 .
.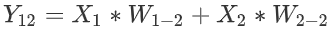 .
. .
.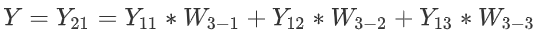 .
. 的最小值點,並且求出最小值。
的最小值點,並且求出最小值。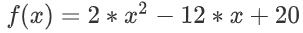 影像如下:
影像如下: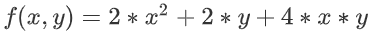
 中,
中,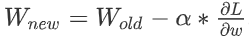 .
. ,原始點此時針對
,原始點此時針對 .
. 表達的含義就是沿著
表達的含義就是沿著  .
.

