第一次OOP作業-Blog總結
- 2021 年 4 月 4 日
- 筆記
前言
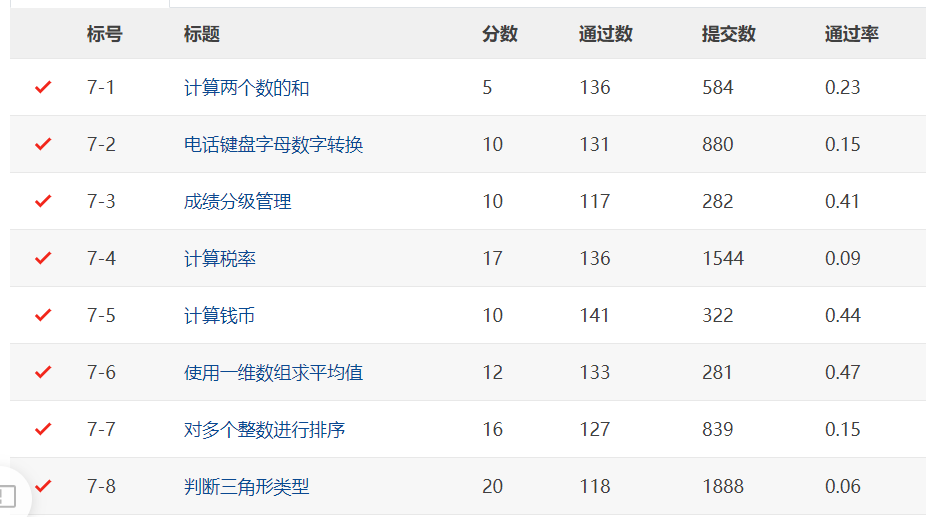
- 第一次作業一共八道題,此次作業也是這三次作業中最接近面向過程程式設計的題目集,整體難度偏低,總耗時1.5h,主要的知識點在熟悉Java的語法上,整體題目的邏輯非常清晰簡單,但最後一個判斷三角形類型中有一些小坑(踩進去以後才發現原來是輕敵了)。
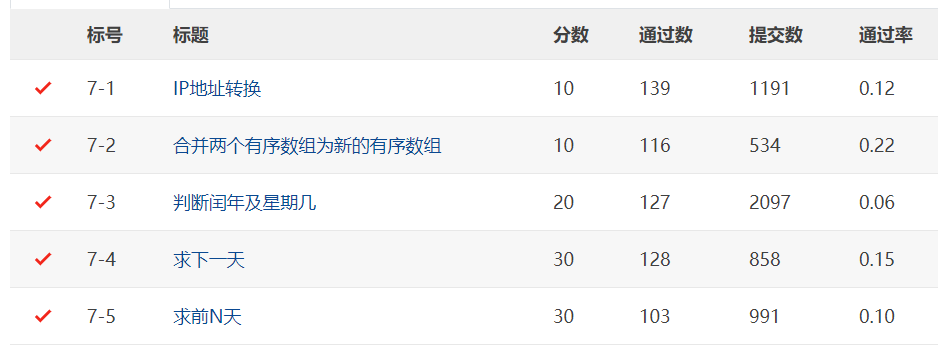
- 第二次題目集的考察內容主要為類和對象的設計,此次題目集開始培養我們的面向對象思維,整體題目難度偏中等,一共五道題,耗時3h,主要卡在求前n天的演算法設計,其中忽略了一些特殊情況。
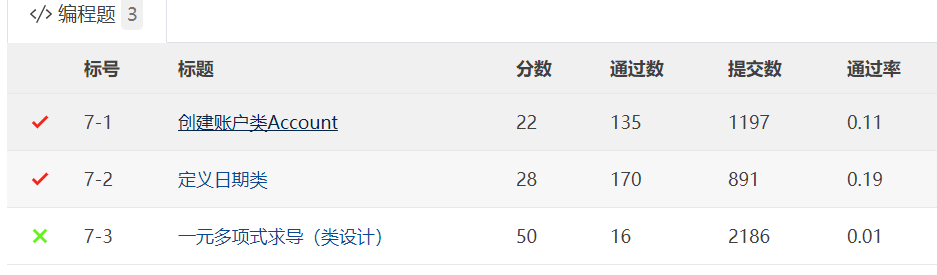
- 第三次題目集可以說是這三次中最難的一次了,一共三道題,前兩道是那種題目要求清晰,設計思路明顯的題,所以很快就做完了。最最最上頭的還是最後一道題,一元多項式的求導,前前後後一共花了四個晚上,但是有一個5分的測試點(合法性)一直過不去,後來也在嘗試寫能夠覆蓋所有類型的正則,但是這一點還是優化失敗了,後面會著重說明解題與優化其他點的思路:).
設計與分析
題目集01 7-8 判斷三角形類型
- 第一次作業判斷三角形類型,按照大學之前積累的關於圖形的知識,其實就可以根據邊的關係判斷此三角形的類型(但是,這是我們的判斷),對於機器內部,可不是這樣的,其中一個直角三角形的判定測試點一直過不去,按照正常思維,只要任意兩條邊的平方和等於第三邊,我們就默認它為直角三角形.But對於無理數而言,這個等式有時是不成立的,所以在這種情況下,只有對相應的值取精度判定,例如:(a*a+b*b-c*c<1e^-2),這裡的1e^-2就是精度,加上這個條件後,直角三角形才能被判定(太能卡了,這裡一直迷惑:)).
- 此外,這裡判定三角形的條件if的先後順序也非常重要,有一些相類似的判定條件,如果順序放錯了,結果可能也會出錯。例如:判斷等腰三角形的條件放在了判斷等腰直角三角形的前面,判斷直角三角形的條件放在了判斷等腰直角三角形的前面,最後的結果雖然在數學層面來說可能是對的,但是對於此題目的要求卻有可能達不到.對於第一種情況,三條邊的長度可以分別為根號2,根號2,2,判斷的結果為等腰三角形,但是對於題目來說他就是等腰直角三角形,第二個就不做贅述了,還有其他的組合可能,都會出現類似的需求錯誤。
- SourceMonitor分析結果
Percent Branch Statements 0.0
Method Call Statements 18
Percent Lines with Comments 5.1
Classes and Interfaces 1
Methods per Class 4.00
Average Statements per Method 3.75
Line Number of Most Complex Method 6
Name of Most Complex Method Main.main()
Maximum Complexity 1
Line Number of Deepest Block 22
Maximum Block Depth 5
Average Block Depth 2.70
Average Complexity 1.00
- Most Complex Methods in 1 Class(es)
-
Complexity, Statements, Max Depth, Calls
1, 6, 2, 4
UML類圖

判斷的條件均寫在了方法里,這次沒有做類的設計,將方法寫在了主類中,判斷用了多重if嵌套,其實邏輯很清晰,就只要注意直角三角形判斷的精度和判斷的順序,這道題就可以完美解決啦。
題目集02 7-1 IP地址轉換
- 這道題其實就已經可以用到正則表達式的知識了,題目的輸入要求很簡單,但是如果用String自帶的charAt或類似的方法判斷輸入是否合法,可能就比較冗餘了,
Regex="[0|1]{32}". - 接下來就是對字元串的操作了,這裡有一個比較大的坑,就是在接收輸入的時候得是接收nextLine()的輸入,不然如果輸入空字元,這時候接收的還是next(),這時候程式不會輸出WrongFormat,而會一直等待輸入。而如果接收的是nextLine(),這時候輸入回車,程式將會直接輸出WrongFormat。
- 這裡想稍微討論一下解決字元串轉換的問題(這裡一定有更高效的演算法來處理,給大夥分享一下我的拙見),我用的是Integer內帶的parseInt方法和String類內部的SubString處理的規範字元串

- 這裡用的還是面向過程的思維,但是這其實是進位轉換的一個過程,查到的資料內部還有位操作符的概念=w=。
題目集02 7-4求下一天
- 題目要求不允許使用Java中的日期相關的類和方法,並且給我們提供了幾個必須實現的方法。

- 先說一下這個合法性吧,在題目提供的合法性範圍內,年份月份和日期都很明確了,所以在寫checkInputValidity方法的時候按理來說就是照著抄的,但是筆者在寫的時候忽略了一個問題,每個月他的日期並不是在1到31之間就是合法的,其中一三五七八十臘月都是31天,四六七九十一月都是30天,二月根據是否為閏年,判斷為28天還是29天。對於每月多少天的設計,我的想法是封裝在一個方法內部設計在一個dayPerMonth方法來簡化判斷操作,方法內部使用Switch判斷(剛開始用if else語句判斷,好傢夥,圈複雜度直接起飛),這裡還可以使用數組來存每個月對應的天數,在對應的閏年將二月份的天數改一下就好了.

- 接下來就是求規定日期的下一天的演算法設計了,這裡筆者是先考慮各種特殊情況,例如12月的最後一天,每個月的最後一天,最後才是考慮一般的情況,這裡邏輯比較簡單,就不做贅述了。

- SourceMonitor分析結果
Percent Branch Statements 49.0
Method Call Statements 10
Percent Lines with Comments 9.1
Classes and Interfaces 1
Methods per Class 4.00
Average Statements per Method 9.50
Line Number of Most Complex Method 40
Name of Most Complex Method isLeapYear().if(()
Maximum Complexity 2
Line Number of Deepest Block 19
Maximum Block Depth 3
Average Block Depth 1.37
Average Complexity 1.50
Most Complex Methods in 2 Class(es):
Complexity, Statements, Max Depth, Calls
isLeapYear().if(() 2, 3, 2, 0
Main.main() 1, 6, 2, 4
UML類圖

題目集02 7-5 求前N天
- 這裡的其他方法相較題目四都無區別,唯一有區別的就是,上道題的求下一天變成了求前N天,這時考慮的範圍就要稍微擴大一點了,需要判斷N天前是否跨年,是否跨月了,但是思維沒有發生太大的改觀,都是先處理特殊情況,再處理一般情況,這裡唯一踩過的坑就是在判斷差值的時候,把judge=0的情況判斷在else中,導致需求輸出0天前,系統輸出的是Wrong Format.

- 其實這裡用類的設計思維可以使得程式變得更加簡潔明了,如果按照這個設計風格的話,就還是停留在面向過程程式設計的層次了,這個在後面的題目集中進行了修改。
- SourceMonitor分析結果
Percent Branch Statements 45.6
Method Call Statements 15
Percent Lines with Comments 16.7
Classes and Interfaces 1
Methods per Class 6.00
Average Statements per Method 8.33
Line Number of Most Complex Method 16
Name of Most Complex Method Main.DaysAgo()
Maximum Complexity 7
Line Number of Deepest Block 71
Maximum Block Depth 4
Average Block Depth 1.82
Average Complexity 3.33
Most Complex Methods in 2 Class(es):
Complexity, Statements, Max Depth, Calls
isValid().if(() 2, 3, 2, 0
Main.DaysAgo() 7, 10, 3, 9
Main.main() 1, 7, 2, 5
UML類圖

題目集03 7-2 定義日期類 求下一天
- 這幾次的日期題採用了迭代升級難度的方式,一步步把我們面向過程設計的思想帶到面向對象設計來.題目給出了類圖,不得不說看著類圖寫程式,思路是真的清晰,不管是寫部分功能也好,寫工程項目設計也罷,一種良好的設計模式總是能讓設計事半功倍,所以在處理問題前至少需要花70%的時間來設計類圖.

- Date類中要求設計的每月多少天的數組,簡化了DayPerMonth中的操作與判斷,在使用時,只需要判斷該年是否為閏年,將數組中第三個元素改為29or28就行了.
private int[] mon_maxnum = new int[]{0,31,28,31,30,31,30,31,31,30,31,30,31};

- SourceMonitor分析結果
Percent Branch Statements 17.9
Method Call Statements 9
Percent Lines with Comments 4.6
Classes and Interfaces 2
Methods per Class 6.50
Average Statements per Method 3.00
Line Number of Most Complex Method 64
Name of Most Complex Method isLeapYear().if(()
Maximum Complexity 2
Line Number of Deepest Block 31
Maximum Block Depth 3
Average Block Depth 1.07
Average Complexity 1.50
Most Complex Methods in 2 Class(es):
Complexity, Statements, Max Depth, Calls
isLeapYear().if(() 2, 3, 2, 0
Main.main() 1, 7, 2, 4
UML類圖

-
在大多數情況下,需要儘可能完美的解決一個問題,一個類其實是不太妥當的,這很可能就違背了類的單一職責原則(這個原則在規範思想的時候真的超管用!!)

-
在我的理解中,對此題進一步的優化就是,將Date中處理日期,輸出日期的方法,放到另外一個類中,這個類里有Date的實例化對象(這個在下一題處理多項式的項中會有比較好的體現),專門用來處理用戶自定義類Date裡邊的數據,提高了程式的可擴展性.
題目集03 7-3 一元多項式求導(類設計)
- 說實話一開始讀完這個OO作業3-3作業指導書,我是毫無頭緒的,但是對於這個業務背景我們又是非常熟悉的,什麼是帶符號整數,冪函數,項,相應的表達式以及對應的求導演算法,我們可以說是知根知底了,但是真的需要將其抽象起來,思維就好像是一片空白.

正則表達式書寫
-
但是冷靜下來,仔細梳理一下,發現也許大體思路很清晰,用戶輸入對應的字元串後,可能其中含有空格,如果有空格的話,後面寫正則需要考慮的情況就多了很多了,所以綜合考量後,決定在主程式中就把空格幹掉!
replaceAll("[ ]", ""),這裡說下我犯的小錯把,這裡一開始正則表達式沒有帶旁邊的中括弧,前面係數字元串里就是一個空格,最後的結果就是,系統不認這個正則,處理後的字元串和處理前的沒區別=w=,好了,接下來就是對正則表達式進行一個合法性判斷,剛開始,我一直糾結什麼樣的表達式才算是合法的,這次的需求分析內只是說有帶符號常數,冪函數,那麼肯定要把相應的項種類設置成對應的類,這樣也方便後面的求導演算法擴展,那麼常數和冪函數的正則表達式都挺好寫的
(這裡的寫法很多,我分享一下我的思路吧) -
常數正則:
"(([+-])?(([1-9][0-9]*)|[0-9]))" -
冪函數正則:
"((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|()))" -
後來想了一下,既然這道題對項的定義內這兩個都有,那麼一個合法的項應該是常數或者冪函數,藉助這個思路,也就順水推舟寫出了多項式的正則了,籠統點理解就是一項or大於一項的正確的項
-
項正則:
"(((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|())))|(([+-])?(([1-9][0-9]*)|[0-9]))" -
多項式正則:
"((((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|())))|(([+-])?(([1-9][0-9]*)|[0-9])))*"
這兩個正則唯一的區別就是:(多了個星號*)
-
如果沒有正則表達式的話,這道題的工作量將難以想像的大了AwA,他就像是總結了這個元素的規則,在編寫前一定一定要儘可能地將所有的條件都考慮到,這樣無論是在判斷,還是在之後的組合優化,都會非常方便。
-
那麼這裡的難點就在於,多項式個相對複雜的正則應該怎麼寫,個人觀點:就像題目集的迭代一樣,在一開始把問題需要解決的各個part細心分析出來,再一步步細化,就有點自頂向下的味道了。多項式->項->(常數,冪函數),一步步的將其簡單化,最後根據相應的需求進行組合就ok啦。
多項式求導
對於這部分的大體思路是:先對項求導,再將項求導後的結果存儲起來,拼接成一個完整的字元串.
但是這裡其實有四個問題需要解決
- 項求導演算法的設計
- 求導前後的元素存儲結構設計
- 如何根據輸入的項創建不同種類的對象
- 如何將求導後的對象按照任務書的需求拼接
項求導演算法的設計
在說設計之前,需要說明的一點就是,因為這裡的各個項的係數測試點內部,有超過Int類型的值測試用例存在,所以這裡的屬性聲明採用BigInteger類型.不然用int型是裝不下二三十位數的:)
– 設置的抽象父類

– 常數項
常數項的求導真的非常簡單,這裡在不考慮常數前符號的情況下,對於任意常數,求導結果都為0

不過在設計常數轉換為字元串的抽象方法實現時,需要考慮到常數的符號,再轉換成相應的字元串

– 冪函數
對冪函數的求導,按照求導演算法,這裡先對係數和指數進行求導操作

比常數要複雜一些,這裡需要對係數和指數的各個情況進行綜合考慮,求導之後若係數為0,則說明係數在處理之前就已經為0了,也就是說這其實是一個不合法的冪函數表達式,在處理這類表達式時,把他看成常數項處理(這裡不管怎麼求導都是0).求導之後若係數不為0,則該表達式為冪函數,我們就創建一個對應冪函數的對象,該方法返回的是一個Factor對象(提一下,這裡的Factor是PowerFunction和ConstantNum的抽象父類),在處理多項式求導的類中運用了這幾個類的多態來解決設計問題.

求導前後的元素存儲結構設計
在設計之初,是想用數組存儲的,但是轉念一想,我需要存儲的是一項項對象,而不是簡單的存儲字元串,如果按照存儲字元串的思維來想的話,又跳轉到面向過程的設計結構了,所以這裡把數組的念頭給打消了,運用了ArrayList<class>來存儲指定類型的對象,ArrayList是一種動態數組,在添加數據時,就不需要考慮會不會溢出了,同時這裡很多封裝的方法(增add刪remove改set查indexof插)使用的也很方便,先按照判斷項的正則將多項式分解為項,均存入Term中,再進行一項項求導,結果存入AfterDev中,細節在下方創建不同種類對象說明.

包括接下來對ArrayList中的對象元素存儲也是使用ArrayList存儲,這兒的處理思想就是按照字元串來處理了,比較好理解。

正則表達式書寫
-
但是冷靜下來,仔細梳理一下,發現也許大體思路很清晰,用戶輸入對應的字元串後,可能其中含有空格,如果有空格的話,後面寫正則需要考慮的情況就多了很多了,所以綜合考量後,決定在主程式中就把空格幹掉!
replaceAll("[ ]", ""),這裡說下我犯的小錯把,這裡一開始正則表達式沒有帶旁邊的中括弧,前面係數字元串里就是一個空格,最後的結果就是,系統不認這個正則,處理後的字元串和處理前的沒區別=w=,好了,接下來就是對正則表達式進行一個合法性判斷,剛開始,我一直糾結什麼樣的表達式才算是合法的,這次的需求分析內只是說有帶符號常數,冪函數,那麼肯定要把相應的項種類設置成對應的類,這樣也方便後面的求導演算法擴展,那麼常數和冪函數的正則表達式都挺好寫的
(這裡的寫法很多,我分享一下我的思路吧) -
常數正則:
"(([+-])?(([1-9][0-9]*)|[0-9]))" -
冪函數正則:
"((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|()))" -
後來想了一下,既然這道題對項的定義內這兩個都有,那麼一個合法的項應該是常數或者冪函數,藉助這個思路,也就順水推舟寫出了多項式的正則了,籠統點理解就是一項or大於一項的正確的項的組合
-
項正則:
"(((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|())))|(([+-])?(([1-9][0-9]*)|[0-9]))" -
多項式正則:
"((((([+-])?([1-9][0-9]*\\*)?))x((([\\^][+-]?[1-9][0-9]*)|())))|(([+-])?(([1-9][0-9]*)|[0-9])))*"
這兩個正則唯一的區別就是:(多了個星號*)
-
如果沒有正則表達式的話,這道題的工作量將難以想像的大了AwA,他就像是總結了這個元素的規則,在編寫前一定一定要儘可能地將所有的條件都考慮到,這樣無論是在判斷,還是在之後的組合優化,都會非常方便。
-
那麼這裡的難點就在於,多項式個相對複雜的正則應該怎麼寫,個人觀點:就像題目集的迭代一樣,在一開始把問題需要解決的各個part細心分析出來,再一步步細化,就有點自頂向下的味道了。多項式->項->(常數,冪函數),一步步的將其簡單化,最後根據相應的需求進行組合就ok啦。
項求導演算法的設計
在說設計之前,需要說明的一點就是,因為這裡的各個項的係數測試點內部,有超過Int類型的值測試用例存在,所以這裡的屬性聲明採用BigInteger類型.不然用int型是裝不下二三十位數的:)
– 設置的抽象父類

– 常數項
常數項的求導真的非常簡單,這裡在不考慮常數前符號的情況下,對於任意常數,求導結果都為0

不過在設計常數轉換為字元串的抽象方法實現時,需要考慮到常數的符號,再轉換成相應的字元串

– 冪函數
對冪函數的求導,按照求導演算法,這裡先對係數和指數進行求導操作

比常數要複雜一些,這裡需要對係數和指數的各個情況進行綜合考慮,求導之後若係數為0,則說明係數在處理之前就已經為0了,也就是說這其實是一個不合法的冪函數表達式,在處理這類表達式時,把他看成常數項處理(這裡不管怎麼求導都是0).求導之後若係數不為0,則該表達式為冪函數,我們就創建一個對應冪函數的對象,該方法返回的是一個Factor對象(提一下,這裡的Factor是PowerFunction和ConstantNum的抽象父類),在處理多項式求導的類中運用了這幾個類的多態來解決設計問題.

求導前後的元素存儲結構設計
在設計之初,是想用數組存儲的,但是轉念一想,我需要存儲的是一項項對象,而不是簡單的存儲字元串,如果按照存儲字元串的思維來想的話,又跳轉到面向過程的設計結構了,所以這裡把數組的念頭給打消了,運用了ArrayList<class>來存儲指定類型的對象,ArrayList是一種動態數組,在添加數據時,就不需要考慮會不會溢出了,同時這裡很多封裝的方法(增add刪remove改set查indexof插)使用的也很方便,先按照判斷項的正則將多項式分解為項,均存入Term中,再進行一項項求導,結果存入AfterDev中,細節在下方創建不同種類對象說明.

包括接下來對ArrayList中的對象元素存儲也是使用ArrayList存儲,這兒的處理思想就是按照字元串來處理了,比較好理解。

如何根據輸入的項創建不同種類的對象
UML類圖

- 除了主類以外,這裡一共有五個類,一個抽象類,四個實體類,其中ConstantNum(常數)與PowerFunction(冪函數)類繼承抽象類Factor,polynomial類是多項式類,內部寫了大致的處理框架與規範輸出框架,具體的處理細節在DealInputItems中的DealItems方法,返回的是Factor類型的值,因為在處理項之前並不知道是常數項還是冪函數項,所以將返回值設置為兩個類的父類,這樣在polynomial類中實現多項式求導演算法就可以藉助DealInputItem的實體類完成處理了。

現在我分享一下我處理這個問題的思路吧,這裡用排列組合的方式大致分出了冪函數的所有類型,根據有無正負號,有無指數,係數是否為1(這裡的前提是不為0),分為8種情況,這裡我用數組將各種情況的正則表達式存儲起來,用於判斷該項若是冪函數,應該歸類到哪類的冪函數(這裡的實現方法可能相對效率低,後面迭代會去學著用Map類中的鍵值對思想來實現,因為之前查閱資料綜合分析之後,發現Map和Tree的思想更適合該類題目的設計)

該函數的主邏輯思維大致如下:
- 根據冪函數正則與常數正則判斷該項的類型.
- 若匹配常數,則直接返回ConstantNum類的對象.將係數直接賦值。
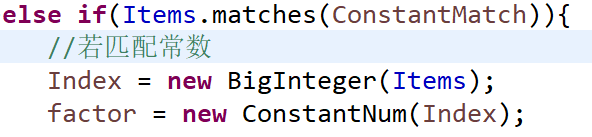
若匹配的是冪函數,則對該項進行依次的正則匹配,此時的係數與指數的賦值與分配就有所差異了。
對於沒有係數和指數的冪函數,對係數和指數的賦值創建對象就很簡單了,可以直接賦值,就像這樣

那麼大部分情況其實還是需要我們去分割字元串的,在有係數或者有指數的情況下,我們需要將指係數分離,藉助String類中的split方法,取得相應的值,再賦給對應參數,break後返回相應Factor對象。

完成上面這一步後,邏輯就返回到polynomial類中的求導演算法,由於返回的是Factor類對象,所以在判斷求導之前,需要判斷返回的對象是哪一個類的實例化,再創建實例化的對象,調用求導方法

最後返回的值通過AfterDev存儲

如何將求導後的對象按照任務書的需求拼接
本來以為通過上面的步驟之後,就已經可以達到預期了,直到我碰到了這個測試用例

如果第一眼看上去,憑感覺這個結果肯定是錯誤的,但是仔細一分析,求導演算法是對的,但是這個結果顯示在螢幕上就是我們不願意看到的結果

後來我想弄明白到底是哪裡出錯的時候,我決定在項和項之間加上空格判斷.

仔細查看每一項的求導結果,都是對的,大數測試也是對的,唯一的錯誤點在於,當後面一項為正數時,前一項與後一項之間沒有「+」號,導致所有的項輸出都擠在一起了,那麼怎麼判斷這些項的正負呢(這其實也就是寫的大方面正則的一個特例),通過這個判斷,決定相應的項前需不需要加上「+」號。

接上正號後,輸出的結果是這樣的

好傢夥,原本以為到這裡就結束了,但是本著好奇的心,我對輸入輸出規則的每一項進行了校驗,結果證明我還是忽略了一些要素.

可以看到當求導結果為0時,結果並沒有按照任務指導書上說的那樣”不顯示“,反而非常倔強彈出來個0,那麼我想到的是,在輸出之前,對每一項做一個equals檢測,如果為”0″(字元串),就把他remove.

處理後的結果是這樣的

但是當整個表達式的求導結果為”0″時

我的判定直接把所有的項都移除了(不得不說這就好像是面向需求編程=w=)
於是就有了下面這項操作

- 雖然整體結果是幾乎成功把所有的條件都考慮清楚並解決的,但是實際上這樣寫,複雜度會升的很快,同時程式碼也比較冗餘,需要一遍遍的去應對出現的各種狀況,優化的改進就需要在類的設計上對各個情況先進行處理(在生成實例化對象之前,就對該項的每一種情況進行分析返回),或者,換一種思路,使用Map,是一種映射表的概念,指數作為鍵,係數作為值,對每一項的求導值做一個映射(在題目集結束後參考各路大佬後得到了比較新穎的idea),不過自始自終這些分享只能作為參考,真正的融會貫通還需要自己思考,在已有的情況上進行不斷的優化改進。
SourceMonitor分析結果
Percent Branch Statements 21.3
Method Call Statements 59
Percent Lines with Comments 12.3
Classes and Interfaces 5
Methods per Class 5.00
Average Statements per Method 6.44
Line Number of Most Complex Method 231
Name of Most Complex Method DealInputItems.DealItems()
Maximum Complexity 12
Line Number of Deepest Block 257
Maximum Block Depth 6
Average Block Depth 1.96
Average Complexity 2.23
Most Complex Methods in 4 Class(es):
| FunctionName | Complexity | Statements | Max Depth | Calls |
|---|---|---|---|---|
| ConstantNum.ConstantNum() | 1 | 1 | 2 | 0 |
| ConstantNum.ConstantNum() | 1 | 0 | 0 | 0 |
| ConstantNum.Derivation() | 1 | 1 | 2 | 0 |
| ConstantNum.getNumber() | 1 | 1 | 2 | 0 |
| ConstantNum.ParseToString() | 4 | 6 | 3 | 4 |
| ConstantNum.setNumber() | 1 | 1 | 2 | 0 |
| DealInputItems.DealItems() | 12 | 48 | 6 | 10 |
| Main.main() | 3 | 7 | 3 | 4 |
| polynomial.getPoly() | 1 | 1 | 2 | 0 |
| polynomial.isPolynomial() | 1 | 3 | 2 | 3 |
| polynomial.polynomial() | 1 | 1 | 2 | 0 |
| polynomial.polynomial() | 1 | 0 | 0 | 0 |
| polynomial.setPoly() | 1 | 1 | 2 | 0 |
總結
- 這其實也不是第一次接觸正則表達式了,之前在做C語言課設的時候就已經做到了所有的輸入資訊校驗,真的非常方便,不僅能規範輸入,還能降低因為誤輸入而導致的程式崩潰,方便處理傳入的資訊。那麼在接下來的OOP題目集中,正則的使用範圍將會越來越廣,優勢也愈加明顯。
- 另外,在程式設計基礎語言的函數模組化設計的基礎思維上,面向對象編程不斷的強化模組化與面向對象化的思想,從一Main到底,程式碼紊亂->Main最簡潔,函數內部瘋狂套娃調用->各個模組各司其職,粘連性低,易維護擴展。
- 大部分題目其實如果真的只想達到需求的話,完全可以按照面向對象語言的思想一個個列出來,但是Java這門語言為我們提供各種強大的工具與語法,讓我們能夠以更加清晰的目光去看待問題中抽象的事物,抽象事物具體化。
- 在看到測試點一個個的由綠變紅,心中充滿喜悅的同時,其實也是對一次次優化的肯定,兩個小時連續提交十來二十次也不是什麼怪事,找到問題,分析問題,解決問題,總結復盤與提升才是真正的挑戰!












