在Python里，用股票案例講描述性統計分析方法（內容來自我的書）
描述性統計是數學統計分析里的一種方法，通過這種統計方法，能分析出數據整體狀況以及數據間的關聯。在這部分里，將用股票數據為樣本，以matplotlib類為可視化工具，講述描述性統計里常用指標的計算方法和含義。
1 平均數、中位數和百分位數
平均數比較好理解，是樣本的和除以樣本的個數。
中位數也叫中值，假設樣本個數是奇數，那麼數據按順序排列後處於居中位置的數則是中位數，如果樣本個數是偶數，那麼排序後，中間兩個數據的均值則是中位數。通俗地講，在樣本數據里，有一半的樣本比中位數大，有一半比它小。
把中位數的概念擴展一下，即可得到百分位數。比如第25百分位數則表示，樣本數據里，有25%的數據小於等於它，而75%的數據大於它。在實際項目里，還會把第25百分位數、中位數和第75百分位數組合起來形成四分位數，因為通過這些數，能把樣本一分為四。其中第25百分位數也叫下四分位數，第75百分位數也叫上四分位數。
理解概念後，在如下的CalAvgMore.py範例中，將以股票收盤價為例，演示平均數、中位數和四分位數的求法。
1 #coding=utf-8
2 import pandas as pd
3 filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
4 df = pd.read_csv(filename,encoding='gbk') #讀取數據到DataFrame
5 print(df['Close'].mean()) #輸出收盤價的平均值
6 print(df['Close'].median()) #輸出收盤價的中位數
7 print(df['Close'].quantile(0.5)) #輸出收盤價第50百分位數
8 print(df['Close'].quantile(0.25)) #輸出收盤價第25百分位數
9 print(df['Close'].quantile(0.75)) #輸出收盤價第75百分位數在進行數據分析時，一般會先從csv文件等數據源里獲取樣本，獲取後用表格類型的DataFrame對象來存儲，所以在第3行和第4行里，演示從指定csv文件里得到數據並通過read_csv導入到DataFrame類型對象的做法，這裡用到csv是由9.1.4部分的StoreStockToMySQL範例生成的。
Pandas庫的DataFrame對象已經封裝了求各種統計數據的方法，具體而言，能通過第5行的mean方法求平均值，在調用時，還可以用諸如df[‘Close’]的樣式，指定針對哪列數據計算。通過第6行的median方法，能計算指定列的中位數。
在第7行到第9行的程式碼里，是通過 quantile方法求百分位數，比如第7行的參數是0.5，則求第50的百分位數。運行本範例，能看到如下的輸出結果，其中第2行輸出的中位數和第3行輸出的第50百分位數是一個結果。
2 用箱狀圖展示分位數
箱狀圖能以可視化的方式，形象地展示平均數和諸多分位數。在如下的BoxPlotDemo.py範例中，將還是以股票收盤價為例，展示箱狀圖的繪製技巧，從中大家能進一步了解分位數的概念。
1 #coding=utf-8
2 import pandas as pd
3 import matplotlib.pyplot as plt
4 filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
5 df = pd.read_csv(filename,encoding='gbk') #讀取數據到DataFrame
6 #繪製箱狀圖
7 df['Close'].plot.box(patch_artist=True,notch = True)
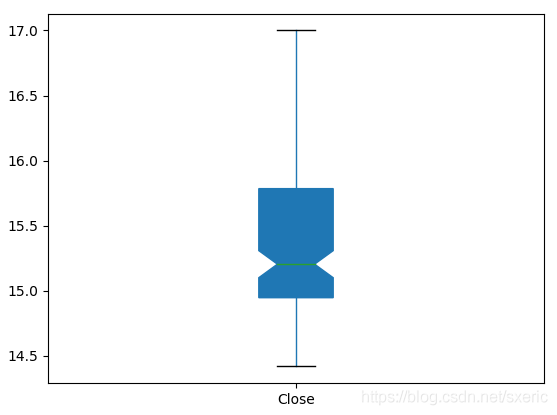
8 plt.show()在程式碼的第5行里，還是通過read_csv方法把csv文件數據讀到df對象，之後，是通過第7行的plot.box方法，繪製「收盤價」的箱狀圖，運行本範例後，能看到如下圖所示的效果。
在第7行繪製箱狀圖時傳入了兩個參數，其中patch_artist=True表示需要填充箱體的顏色，用notch = True表示以凹口的方式展示箱狀圖。從上述箱狀圖裡，能形象地看到最高和最低的值，以及第25、第50和第75百分位數的值，由此更能形象地看到「收盤價」樣本數的聚集區間。
3 統計極差、方差和標準差
在統計學裡，一般用這三個指標來衡量樣本數據的離散度，即衡量樣本數對於中心位置（一般是平均數）的偏離程度。
其中，極差的演算法比較簡單，是樣本里最大值和最小值的差，而方差是每個樣本值與全體樣本值的平均數之差的平方值的平均數，標準差則是方差的平方根。在如下的CalAlias.py範例中，將演示這三個值的獲取方式。
1 #coding=utf-8
2 import pandas as pd
3 filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
4 df = pd.read_csv(filename,encoding='gbk') #讀取數據到DataFrame
5 print(df['Close'].max() - df['Close'].min()) #求極差
6 print(df['Close'].var()) #求方差
7 print(df['Close'].std()) #求標準差在第5行里，是通過最大值減最小值的方法算出了極差，在第6行里，通過var方法計算了方差，第7行則通過std方法求標準差。
本文出自我寫的書： Python爬蟲、數據分析與可視化：工具詳解與案例實戰，//item.jd.com/10023983398756.html
請大家關注我的公眾號：一起進步，一起掙錢，在本公眾號里，會有很多精彩文章。
