數理統計7：矩法估計（MM）、極大似然估計（MLE），定時截尾實驗

在上一篇文章的最後，我們指出，參數估計是不可能窮盡討論的，要想對各種各樣的參數作出估計，就需要一定的參數估計方法。今天我們將討論常用的點估計方法：矩估計、極大似然估計，它們各有優劣，但都很重要。由於本系列為我獨自完成的，缺少審閱，如果有任何錯誤，歡迎在評論區中指出，謝謝！

Part 1：矩法估計
Part 2：極大似然估計
Part 3：一個例題

Part 1：矩法估計

矩法估計的重點就在於「矩」字，我們知道矩是概率分布的一種數字特徵，可以分為原點矩和中心矩兩種。對於隨機變數\(X\)而言，其\(k\)階原點矩和\(k\)階中心矩為

\[a_k=\mathbb{E}(X^k),\quad m_k=\mathbb{E}[X-\mathbb{E}(X)]^k,
\]

特別地，一階原點矩就是隨機變數的期望，二階中心矩就是隨機變數的方差，由於\(\mathbb{E}(X-\mathbb{E}(X))=0\)，所以我們不定義一階中心矩。

實際生活中，我們不可能了解\(X\)的全貌，也就不可能通過積分來求\(X\)的矩，因而需要通過樣本\((X_1,\cdots,X_n)\)來估計總體矩。一般地，由\(n\)個樣本計算出的樣本\(k\)階原點矩和樣本\(k\)階中心矩分別是

\[a_{n,k}=\frac{1}{n}\sum_{j=1}^{n}X_j^k,\quad m_{n,k}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^k.
\]

顯然，它們都是統計量，因為給出樣本之後它們都是可計算的。形式上，樣本矩是對總體矩中元素的直接替換後求平均，因此總是比較容易計算的。容易驗證，\(a_{n,k}\)是\(a_k\)的無偏估計，但\(m_{n,k}\)則不是。

特別地，\(a_{n,1}=\bar X\)，

\[m_{n,2}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^2=\frac{n-1}{n}S^2\xlongequal{def}S_n^2,
\]

一階樣本原點矩就是樣本均值，二階樣本中心矩卻不是樣本方差，而需要經過一定的調整，這點務必注意。這裡也可以看到，由於\(S^2\)是\(\mathbb{D}(X)\)的無偏估計，\(S_n^2\)自然就不是了。

下面給出矩法估計的定義：設有總體分布族\(X\sim f(x;\theta)\)，這裡\(\theta\)是參數，\(g(\theta)\)是參數函數。如果\(g(\theta)\)可以被表示為某些總體矩的函數：

\[g(\theta)=G(a_1,\cdots,a_k,m_2,\cdots,m_k),
\]

則從\(X\)中抽取的簡單隨機樣本可以計算相應的樣本原點矩\(a_{n,k}\)和中心矩\(m_{n,k}\)，替換掉\(G\)中的總體矩，就得到矩估計量為

\[\hat g(\boldsymbol{X})=G(a_{n,1},\cdots,a_{n,k},m_{n,2},\cdots,m_{n,k}).
\]

看著很長的一段定義，其實體現出的思想很簡單，就是將待估參數寫成矩的函數，再用樣本矩替換總體矩得到矩估計量。並且實踐中，還可以遵循以下的原則：

如果低階矩可以解決問題，不要用高階矩。這是因為低階矩的計算總是比高階矩更容易的。
如果原點矩可以解決問題，不要用中心矩。這是因為中心矩既不好算，還是有偏估計。

運用矩法估計，我們可以很容易地得到一些總體矩存在的分布的參數點估計。下面舉書上的例子——Maxwell分布為例，其總體密度為

\[p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}.
\]

現在要對此參數\(g(\theta)=1/\theta\)作估計。用矩法估計的話，我們要求出總體矩，按照上面的原則，假設\(X\)服從Maxwell分布，則

\[a_1=\mathbb{E}(X)=2\sqrt{\frac{\theta}{\pi}}\int_0^{\infty}xe^{-\theta x^2}\mathrm{d}x=\frac{1}{\sqrt{\pi\theta}},
\]

顯然有

\[g(\theta)=\frac{1}{\theta}=a_1^2\pi,
\]

所以其矩估計量為\(\hat g_1(\boldsymbol{X})=\pi\bar X^2\)，簡單快捷地求出了矩估計量。

但是，矩估計量唯一嗎？我們不妨再往上計算一層，計算其二階原點矩\(a_2\)，它的計算比\(a_1\)稍微複雜一些，有

\[\begin{aligned}
a_2&=\mathbb{E}(X^2)=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty x^2e^{-\theta x^2}\mathrm{d}x\\
&=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty -\frac{x}{2\theta}\mathrm{d}(e^{-\theta x^2})\\
&=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty e^{-\theta x^2}\cdot\frac{1}{2\theta}\mathrm{d}x\\
&=\frac{1}{2\theta},\\
g(\theta)&=\frac{1}{\theta}=2a_2,
\end{aligned}
\]

從這個角度來看，其矩估計量為\(\hat g_2(\boldsymbol{X})=\frac{2}{n}\sum_{j=1}^n X_j^2\)。

你不能說哪一種矩估計量錯了，因為它們都是基於矩法計算得到的合理矩估計量，但是\(\hat g_1\ne \hat g_2\)是顯然的，所以矩估計量是不唯一的。另外，由於兩個矩估計量用到的都是原點矩，且次數都是一次，所以它們都是無偏的。這是矩估計的缺點之一——即得到的估計量不唯一，哪一個更好還有待於實踐的選擇。

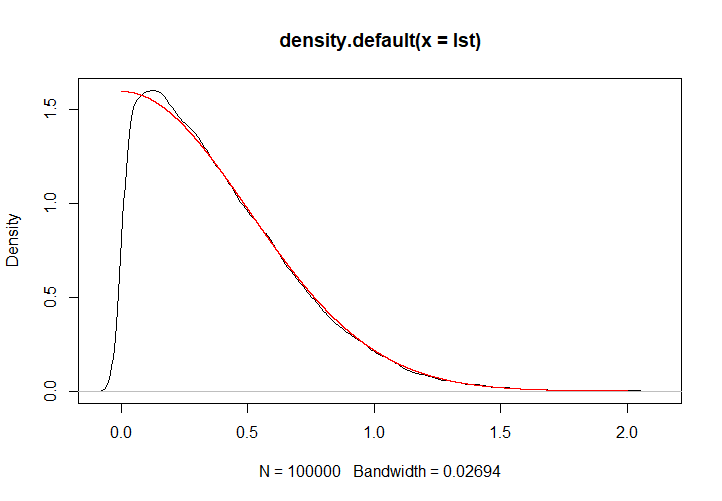
現在我們來檢驗一下哪個統計量效果更好一些，假設參數\(\theta=2\)。為此，我們需要設法從Maxwell分布中抽樣，抽取100000個樣本，分成50組，每一組包含2000個樣本。

如何從Maxwell分布中抽樣是一個需要考慮的問題，使用MCMC抽樣法，下面的函數是用於從Maxwell分布中抽樣的：
p <- function(x, theta){
# Maxwell分布的密度函數，無正則化因子
return(exp(-theta*(x^2)))
}

maxwell <- function(n, theta){
# 從參數為theta的Maxwell分布中抽取n個樣本
buffer <- 10000
samples <- c()
x <- 1 # 初始值
for (i in 1:(buffer+n)){
 y <- runif(1, x-0.5, x+0.5)  # 極小鄰域
 h <- runif(1)
 if (y > 0 && h < p(y,theta)/p(x,theta)){
   x <- y
 }
 if (i > buffer){
   samples[i-buffer] <- x
 }
}
return(samples)
}
此程式是能夠正常運行的，下圖中，黑色為抽樣核密度，紅色為實際的密度曲線。

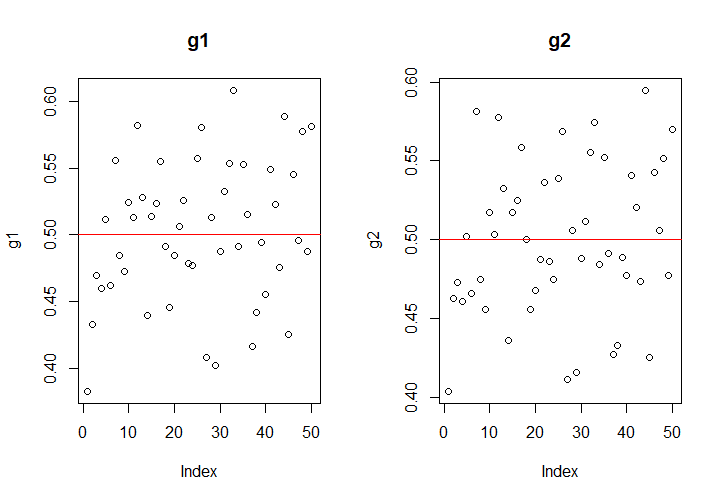
對於2000個一組的樣本，計算其估計量的值，結果如下：

在樣本容量為2000時，兩個估計量的表現類似，精度都在\(\pm 0.1\)左右，不能說有多好；但對於我們的100000個樣本，如果一起計算，則

\[\hat g_1(\boldsymbol{X})=0.5000618,\\
\hat g_2(\boldsymbol{X})=0.499744,
\]

效果都不錯。

事實上，\(a_{n,k}\)總是\(a_k\)的無偏估計、強相合估計，所以這也成為了矩估計的優點，只要選擇的矩是原點矩的話。但是，我們也可以看到即使樣本容量多達2000，矩估計也偶然會出現20%的較大誤差，因此矩估計的精度是難以解決的痛；並且，矩法估計要求總體矩一定是要存在的，對於柯西分布這類奇形怪狀的分布，矩法估計就沒法使用。

Part 2：極大似然估計

極大似然估計是另外一種參數點估計的方法，它採用的思路與矩估計的「直接替代」不同。矩估計更像是一種貪圖方便的做法，採用直接替代法而不顧後果，這樣雖然有無偏性和強相合性作為保證，但精度卻無法考慮。極大似然估計源於事情發生的可能性，它總是在可選擇的參數中，選擇最有可能導致這個抽樣結果發生的參數，作為參數的估計量。

如何量度這種事情發生的可能性呢？我們以離散情況為例，離散情況下，如果你抽取了一組樣本\(\boldsymbol{X}=(X_1,\cdots,X_n)\)，它的觀測值是\((x_1,\cdots,x_n)\)，則在參數為\(\theta\)的情況下，這組觀測值發生的概率就是

\[\mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta),
\]

既然不同的\(\theta\)對應著不同的發生概率，在發生概率和\(\theta\)之間就存在一個對應關係，這個關係就稱為似然函數，記作\(L(\theta)\)，即

\[L(\theta)=\mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta).
\]

極大似然估計要做的，就是找到一個\(\theta\)使得\(L(\theta)\)最大，就這麼簡單。如果對於連續的情況，則用聯合密度函數表示這個聯合概率函數即可。總而言之，極大似然估計的要點，就是先寫出似然函數來，似然函數與聯合概率函數是形式上一致的，只是主元從\(\boldsymbol{x}\)變成了待估參數\(\theta\)。

依然以Maxwell分布為例，它的總體密度為

\[p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}.
\]

所以似然函數就是聯合密度函數的形式，寫成

\[\begin{aligned}
L(\theta)&=2^n\left(\frac{\theta}{\pi} \right)^{n/2}\exp\left(-\theta\sum_{j=1}^n x_j^2 \right)I_{x_{(1)}>0}.
\end{aligned}
\]

要如何對這個函數求\(\theta\)的最大值？既然這裡\(L(\theta)\)是可導的，顯然對\(\theta\)求導最方便，但是對\(L(\theta)\)求導顯然不太方便，注意到使\(L(\theta)\)最小的\(\theta\)值必然也使得\(\ln L(\theta)\)最小，所以我們完全可以對似然函數的對數求導。這個技巧過於常用，以至於人們直接給似然函數的對數\(\ln L(\theta)\)起了一個專門的名字：對數似然函數，記作\(l(\theta)\)。由於聯合密度函數是總體密度的乘積，對數似然就是總體密度對數之和，經過降次，求導肯定更容易了。

在這裡，

\[l(\theta)=n\ln 2+\frac{n}{2}\ln\theta-\frac{n}{2}\ln \pi-\theta\sum_{j=1}^n x_j^2+\ln I_{x_{(1)}>0}.
\]

和\(\theta\)無關的項可以直接視為常數，所以

\[l(\theta)=C+\frac{n}{2}\ln\theta-\theta\sum_{j=1}^n x_j^2,\\
\frac{\partial l(\theta)}{\partial\theta}=\frac{n}{2\theta}-\sum_{j=1}^n x_j^2.
\]

令這個偏導數為\(0\)，就得到了\(\theta\)的極大似然估計量為

\[\hat\theta_{\text{MLE}}=\frac{n}{2\sum_{j=1}^n X_j^2}.
\]

但是，問題還沒有解決，我們要求的是\((1/\theta)\)的極大似然估計，怎麼把\(\theta\)的極大似然估計給求出來了？其實，參考這裡極大似然估計的來源，只有\(\hat\theta_{\text{MLE}}\)能讓似然函數的偏導數為\(0\)取到最大值，由鏈式法則，也只有\(1/\hat\theta_{\text{MLE}}\)能讓似然函數對\(1/\theta\)的偏導數為\(0\)，因此我們得到極大似然估計一個極為有用的性質：

如果\(\hat\theta\)是\(\theta\)的極大似然估計，則\(g(\hat\theta)\)是\(g(\theta)\)的極大似然估計。

雖然這裡對\(g\)有一定的約束，比如\(g\)可微之類的，但是一般情況下這樣的約束都是可以滿足的。因此，我們得到

\[\left(\frac{1}{\theta} \right)_{\text{MLE}}=\frac{2}{n}\sum_{j=1}^nX_j^2=\hat g_2(\boldsymbol{X}).
\]

可以看到，它的極大似然估計與矩法估計中，二階矩對應的矩法估計一致。

不過實際上，極大似然估計並沒有這麼一帆風順，有時候\(L(\theta),l(\theta)\)不一定可導，導數為\(0\)的點也不一定唯一（這兩種情況一般發生在總體是均勻分布的時候），這時候要根據似然函數的性質靈活選擇極大似然估計量。

需要注意的是，極大似然估計的無偏性、相合性都是沒法保證的，為什麼我們要使用它呢？原因很簡單：它的原理很好解釋，並且效果確實還不錯。

Part 3：一個例題

截尾數據是之前一直被我們忽略的題目，這道題出自習題2的第26題，了解這道題還是很有必要的。

某電子元件服從指數分布\(E(1/\lambda)\)，密度函數為

\[f(x)=\frac{1}{\lambda}e^{-\frac{x}{\lambda}}I_{x>0},
\]

從這批產品中抽取\(n\)個作壽命試驗，規定到第\(r\)個電子元件失效時停止試驗，這樣獲得前\(r\)個次序統計量\(X_{(1)}\le X_{(2)}\le \cdots\le X_{(r)}\)和電子元件的總試驗時間

\[T=\sum_{i=1}^rX_{(i)}+(n-r)X_{(r)}.
\]

第一步，證明\(2T/\lambda \sim \chi^2_{2r}\)，即證明\(T\sim \Gamma(r,\lambda)\)。注意到總體服從的分布是指數分布，具有無記憶性，這是本題考察的一大知識點，因此作如下變換：

\[Z_i=X_{(i)}-X_{(i-1)},\quad i=1,2,\cdots,n,X_{(0)}=0.
\]

這裡要注意，雖然\(X_{(r+1)},\cdots,X_{(n)}\)我們沒有觀測到，但是它們是切實存在的量。\(X_{(1)},\cdots,X_{(n)}\)的聯合密度函數為

\[f(x_{(1)},\cdots,x_{(n)})\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{n}x_{(j)} \right\}I_{0<x_{(1)}\le \cdots\le x_{(n)}},
\]

\(X_{(1)},\cdots,X_{(n)}\)到\(Z_1,\cdots,Z_{n}\)變換的Jacobi行列式為\(|J|=1\)，且\(X_{(j)}=Z_1+\cdots+Z_j\)，所以

\[\begin{aligned}
&\quad g(z_1,z_2,\cdots,z_n)\\
&=\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{n}x_{(j)} \right\}I_{0<x_{(1)}\le \cdots\le x_{(n)}}\\
&=\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^n(n+1-j)z_j \right\}I_{z_1>0,\cdots,z_n>0}\\
&=\prod_{j=1}^n\left(\frac{(n+1-j)}{\lambda}\exp\left\{-\frac{n+1-j}{\lambda} z_j\right\}I_{z_j>0}\right)\\
&=\prod_{j=1}^n g_j(z_j),
\end{aligned}
\]

這裡

\[g_j(z_j)=\frac{(n+1-j)}{\lambda}e^{-\frac{n+1-j}{\lambda}z_j}I_{z_j>0},
\]

所以

\[Z_j\sim E\left(\frac{n+1-j}{\lambda} \right),\quad j=1,\cdots,n.\\
(n+1-j)Z_j\sim E(1/\lambda),\quad j=1,\cdots,n.
\]

於是

\[T=\sum_{i=1}^r X_{(i)}+(n-r)X_{(r)}=\sum_{j=1}^r(n+1-j)Z_j\sim \Gamma(r,1/\lambda).
\]

第二步，尋找\(\lambda\)的極大似然估計量。由於統計量是樣本的函數，而我們實際上沒有獲得\(X_{(r+1)},\cdots,X_{(n)}\)的觀測值，因此我們只能用\(X_{(1)},\cdots,X_{(r)}\)來構造統計量。事實上，我們得出了統計量\(T\)的分布，可以驗證\(T\)是充分的，只要求\((X_{(1)},\cdots,X_{(r)})\)的聯合密度，運用我們在次序統計量處說到的方法，可以得出（忽略示性函數部分）

\[\begin{aligned}
&\quad p(x_{(1)},\cdots,x_{(r)})\\
&=n!p(x_{(1)})\cdots p(x_{(r)})\left(\frac{[1-F(x_{(r)})]^{n-r}}{(n-r)!} \right)\\
&=\frac{n!}{(n-r)!}\frac{1}{\lambda^r}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{r}x_{(j)} \right\}\exp\left\{-\frac{n-r}{\lambda}x_{(r)} \right\}\\
&=\frac{n!}{(n-r)!\lambda^r}\exp\left\{-\frac{1}{\lambda}\left[\sum_{j=1}^rx_{(j)}+(n-r)x_{(r)} \right] \right\}\\
&=\frac{n!}{(n-r)!\lambda^r}e^{-\frac{t}{\lambda}}.
\end{aligned}
\]

因此\(T\)是一個充分統計量。下尋找極大似然估計，對數似然函數為

\[l(\lambda)=\ln\left[\frac{n!}{(n-r)!} \right]-r\ln\lambda-\frac{t}{\lambda},
\]

這裡參數空間（參數的取值範圍）為\(\lambda>0\)。對其求偏導，有

\[\frac{\partial l(\lambda)}{\partial \lambda}=-\frac{r}{\lambda}+\frac{t}{\lambda^2}=0
\]

所以

\[\hat\lambda_{\text{MLE}}=\frac{T}{r}.
\]

如果要求指數分布參數\(1/\lambda\)的估計量，則利用極大似然估計的可映射性，得到

\[\widehat{\left(\frac{1}{\lambda}\right)}_{\text{MLE}}=\frac{r}{T}.
\]

Tags: 基於R語言的數理統計學習指南